Алгоритм

Алгоритм

 Предписание, определяющее содержание
 и последовательность операций,
 переводящих исходные данные
 в искомый результат. 

Правила для всех

12 февраля 1535 года в итальянском городе Болонья царило необычайное оживление. Со всех концов Италии, даже из других стран средневековой Европы сюда съехались математики, искусные вычислители и любители интересных состязаний. В этот день начинался математический турнир.

"Математик Фиоре вызывает на поединок каждого, кто желает состязаться с ним в искусстве решения кубических уравнений. Побеждает тот, кто решит больше задач из числа предложенных его противником", - гласило объявление о правилах.

Вызов Фиоре был принят Николо Тартальей, малоизвестным преподавателем математики.

Он оказался победителем турнира, решив все 30 задач, предложенных Фиоре. Последний же не сумел решить ни одной задачи Тартальи!

Каким же образом Николо Тарталье удалось одержать столь блестящую победу, не оставляющую никаких сомнений в его превосходстве над противником?

Ответ на вопрос дают события, предшествовавшие турниру.

Примерно за десять лет до этого скончался профессор математики Болонского университета Сципион дель Ферро. Незадолго до смерти ему удалось найти общий метод решения труднейшей задачи. Об успешном результате многолетнего труда он сообщил только своему зятю и преемнику по должности Анабеллу делла Нове. Но об этом методе неведомыми путями узнал и неведомый Фиоре. Получив в свои руки правило решения задачи, с которой не могли справиться ни арабы, ни греки, ни ученые средневековой Европы, Фиоре бросил вызов математикам.

Обладание формулой, казалось, гарантировало Фиоре победу, но его уверенность не оправдалась. Против него выступил гениально одаренный Тарталья. Приняв вызов, он решил, что легко победит Фиоре. Но всего за десять дней до турнира узнал, что Фиоре знает метод умершего Сципиона дель Ферро. Тогда Тарталья огромным напряжением ума самостоятельно нашел еще более совершенный метод. С его помощью он одержал блестящую победу на турнире.

Алгоритм Тартальи, усовершенствованный потом итальянским математиком Кардано, сохранился до наших дней в виде общего метода решения кубических уравнений.

Что же такое алгоритм? Что это за универсальный инструмент, помогающий решать задачи?

Наверное, многие из вас восхищались учеными собаками, которые в цирке показывают искусство счета: они "складывают" однозначные числа. Собака лает (повинуясь незаметным для публики сигналам дрессировщика), когда ей показывают цифры: три раза - когда перед ней цифра 3, пять раз - когда видит цифру 5. А если между этими цифрами стоит знак + , собака пролает восемь раз.

Сложение по единицам в данном случае выполняется чисто автоматически, без понимания смысла действий.

Такое сложение - самое простое. Правило его выполнения легче всего запомнить.

"Отложим на счетах столько косточек, сколько единиц в первой цифре, и прибавим к ним число косточек, равное числу единиц второй цифры. После этого сосчитаем сумму". Пользуясь этим правилом, первоклассник складывает одноразрядные числа на школьных счетах. Но в математике вместо слова "правило" говорят "алгоритм". Если решаемую задачу можно сравнить с замком, то алгоритм ее решения - это ключ, открывающий замок.

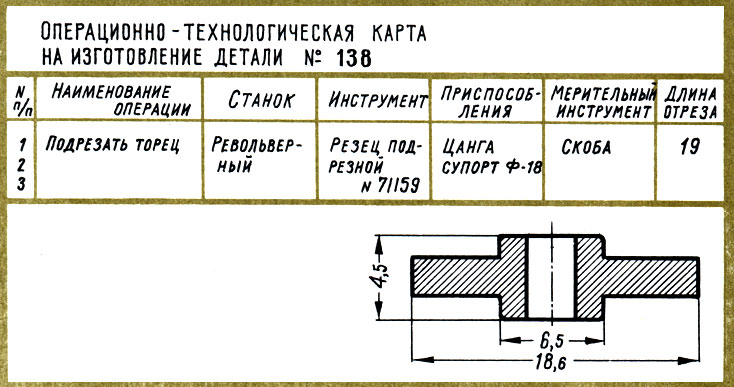
Технологическая карта сопровождает изготовление детали

Технологический бланк сопровождает процесс вычислений

Алгоритмы нужны для решения самых разнообразных задач. Оказывается, математика не может обойтись без своей технологии - способов решения математической задачи.

Технологический процесс решения самой сложной задачи складывается из множества простых операций, из простых элементарных шагов.

Слово "алгоритм", то есть "правило", приобрело теперь чрезвычайно широкий смысл. Это точное указание о порядке решения целого класса сложных задач посредством ряда простых операций. Иными словами, алгоритм - это руководство к действию для решения задач. Его можно даже облечь в форму кратких приказов, которые надо выполнять точно и беспрекословно. Тогда алгоритм послужит вам добросовестным "поводырем" - покажет путь, идя которым можно решить задачу.

Вот пример такого руководства к действию - алгоритм Евклида. Он служит для отыскания общего наибольшего делителя двух чисел а и b. Это руководство состоит из пяти указаний.

Первое. Обозревай оба числа: а и b. Переходи к следующему указанию руководства.

Второе. Сравни обозреваемые числа (а равно b, или а меньше b, или а больше b). Переходи к следующему указанию.

Третье. Если обозреваемые числа равны, то прекрати вычисления, так как каждое из них даст искомый результат. Если числа не равны, переходи к следующему указанию.

Четвертое. Если первое число меньше второго, переставь их местами. Переходи к следующему указанию.

Пятое. Вычитай второе число из первого. Обозревай два числа: вычитаемое и остаток. Переходи к указанию второму.

Итак, после выполнения всех указаний нужно снова вернуться ко второму, затем к третьему, четвертому и т. д., пока обозреваемые числа не станут равны. Тогда вычисление заканчивается. Вместо букв а и b вы можете подставить числа, например 21 и 14. Попробуйте найти для них общий наибольший делитель.

Наши поиски алгоритма напоминают шутку, которую, скорее всего, сочинили математики.

Одного математика спросили, сумеет ли он сварить суп. Он ответил так:

- Сначала я должен сформулировать задачу. Дано: кастрюля, газовая плита, литр воды и концентрат. Задача: сварить суп. Ее можно решить с помощью некоторого построения z. Воду наливают в кастрюлю, кастрюлю ставят на плиту, зажигают газ. Когда вода закипит, добавляют концентрат и через десять минут выключают газ.

- Ну, а если кастрюля уже стоит на плите?

- Тогда задача усложнилась, но ситуация не безнадежна. В данном случае надо выполнить построение z погасить газ, снять с плиты кастрюлю, перелить "оду в другую посуду. Новая задача, таким образом, привела к старой, которую я умею решать. Значит, разрешима и новая. Я сумею сварить суп, если кастрюля уже стоит на плите.

"Стоит ли разводить подобную канитель, - возразите вы, - чтобы найти общий наибольший делитель для таких немудрящих чисел?" Может быть, здесь вы и правы. Но существуют случаи посложнее, чем наш. Для них-то и важно знать алгоритм и уметь его применить.

Всякий алгоритм как руководство к действию должен удовлетворять определенным требованиям. Необходимо, чтобы алгоритм был пригоден для решения не одной какой-нибудь задачи, а для всех задач данного типа. Алгоритм не мог бы служить руководством к действию, если бы годился только для одной пары чисел, например для 21 и 14.

Чтобы найти и разработать алгоритм, нужно иметь обширные знания, затратить много творческого труда. И вот алгоритм найден, порядок решения задачи строго определен. Каждая отдельная вычислительная операция регламентирована, и для решения остается только точно и беспрекословно следовать указаниям. Это может выполнить уже любой человек, действуя совершенно машинально.

Человек работает машинально! Когда мы так говорим, то поневоле сравниваем действия человека с работой машины, и тут же у нас возникает мысль: "А нельзя ли поручить выполнение этой работы машине?"

Оказывается, можно! Подтверждением служат электронные вычислительные машины. Ученые и инженеры умеют теперь автоматизировать решение любой задачи, для решения которой существует алгоритм.

Через всю историю математики красной нитью проходит борьба за алгоритм. Ведь каждый новый алгоритм - это новый путь к решению. И чем проще и короче алгоритм, тем ближе победа над таинственными задачами математики, спрятанными за сложными формулами и уравнениями.

Особое внимание уделяют теперь созданию алгоритмов, специально приспособленных для машинного решения задач. Алгоритмы играют важную роль в вычислительной математике. Можно даже сказать, что все результаты ее состоят в установлении алгоритмов.

Специалисты говорят, что в настоящее время, когда машинная математика быстро развивается и электронные вычислительные машины стали реальностью, все чаще появляется необходимость в нахождении алгоритма, позволяющего решать ту или иную серию задач. Если найден алгоритм, можно составить программу, по которой машина будет решать любую задачу из этой серии. Так как машина считает быстро, а будет считать еще быстрее, то нахождение алгоритма для решения определенного круга задач имеет очень большую ценность. Выгоднее находить общий метод решения для большого числа однородных задач и поручать сам процесс решения машине, чем для каждой задачи искать свой способ и затем решать ее с помощью машины или без нее.

Правила для всех