Вычислительная математика

Вычислительная математика

 Область математики, изучающая методы
 доведения математических задач
 до числового результата и методы
 использования вычислительных средств. 

Добрая фея

Кажется, трудно сомневаться в величии математики - все в мире может быть представлено числом, а всякая в нем перемена выражена математической зависимостью. Недаром поэт сказал: "...все оттенки смысла умное число передает".

Что это такое - математика, которая все может, все постигает, для которой практически нет невозможного?

Фридрих Энгельс говорил: "Математика - это наука, имеющая своим предметом пространственные формы и количественные отношения действительного мира". А знаменитый математик Давид Гильберт с долей превосходства считал, что "математика - это то, что под этим понимают компетентные люди". Другой известный математик, американец Уиллард Гиббс, человек скромный и молчаливый, однажды изрек: "Математика - это язык".

Некоторые утверждают, что в наше время математика, подобно искусству, подмечает явления в реальной жизни, объединяет аналогичные события, процессы и факты, обобщает их.

Но самое близкое духу нашего времени высказывание сделал выдающийся математик современности академик А. Н. Колмогоров: "Математика- это то, посредством чего люди управляют природой и собой".

В свое время великий математик Карл Фридрих Гаусс назвал математику царицей всех наук. Но она скорее добрая фея. От нее можно получить не волшебное средство для решения всех задач, а точные методы. И хотя известно, что и высшая математика берет свое начало от пяти пальцев, математику сегодня можно сравнить с большим городом, окраины которого все время разрастаются, а центр периодически перестраивается, каждый раз по все более ясному плану. Старые кварталы с запутанными переулками сносятся. На их месте прокладываются широкие и удобные улицы.

Прямо скажем, современная математика настолько обширна, разнообразна, что даже гений не в состоянии изучить все ее разделы. Даже самим математикам часто бывает нелегко понять друг друга. Не случайно однажды видный специалист, делегат одного из всемирных конгрессов математики, Сказал: "Мы не можем рассчитывать, что поймем все или хотя бы большую часть того, что здесь услышим".

И все же, поскольку мы живем в эпоху чисел и анализа, в математике, кроме обширной теоретической области, усиленно развивается и область практическая.

Она, по существу, сегодня служит для науки и техники своеобразным инструментом.

Академик А. Н. Крылов, высокообразованный математик, когда-то сказал: "Это есть инструмент такой же, как штангель, зубило, ручник, напильник для слесаря или полусаженок, топор и пила для плотника".

Конечно, математика - инструмент неизмеримо более сложный. Ведь для получения соответствующего решения задачу надо довести до получения числа. А это в наше время не так просто.

Испытание модели в аэродинамической трубе может дать до четверти миллиона точных чисел показателей. Миллиарды показателей поступают ежедневно в бюро прогнозов. А сколько цифрового материала дают переписи, опросы населения, статистический учет в торговле. Даже сугубо теоретические исследования рождения новых тяжелых частиц атомного ядра требуют изучения и обработки 102 тысяч фотоснимков ядерных реакций.

Еще недавно - всего лет 20 назад - нельзя было и думать, чтобы за обозримый промежуток времени рассчитать различные варианты движения космических кораблей, работы атомных реакторов, течение газовых струй в сверхбыстрых потоках, нельзя было провести расчеты внутриатомных сил или ядерных ускорителей.

Теперь подобные расчеты не смущают ученых. Старинную науку математику обогатили и новыми методами, и новыми средствами.

Лишь один пример. Математик Шенкс в свое время потратил жизнь на то, чтобы вычислить число тс с точностью до 707 десятичных знаков. Такой результат получил славу рекорда вычислений XIX века. Недаром на могиле математика лежит плита без единой надписи - на ней изображен только знак тс . Теперь же счетная машина довольно быстро вычисляет это число с точностью до 2035 десятичных знаков!

Благодаря вычислительной технике большое развитие получила вычислительная математика, и математические абстракции стали входить в повседневную жизнь.

Сегодня можно говорить не только о математизации науки, но и о математизации жизни. В этом немалую роль играет и вычислительная математика. Если бы она не позаботилась о совершенствовании методов вычислений, то, наверное, не меньше половины человечества должно было бы непрерывно заниматься вычислениями.

Выдающиеся математики знали: без хорошо разработанной техники вычислений все огромное здание теоретической математики может превратиться в гигантскую изолированную башню. Запертые в ней абстрактные теории были бы обречены на медленное угасание. Животворная связь теоретической математики с практикой, осуществляемая через вычислительную математику и вычислительную технику, помогает человеку в его практической деятельности и двигает вперед математическую науку.

Сократить путь от сложных математических уравнений до конкретного числа, ускорить движение чисел со ступеньки на ступеньку и освободить человека (проводника чисел) от утомительной работы - вот постоянный девиз творцов вычислительной математики.

Поучительна история вычислительной математики. Но, к сожалению, за недостатком места мы не можем о ней рассказать более или менее полно и вынуждены дать всего лишь несколько набросков, небольшой эскиз.

Греческие астрономы использовали математические методы для изучения законов движения небесных светил. В связи с этим они много сделали для развития вычислительной математики.

Труды греческих астрономов завершаются исследованиями знаменитого александрийского математика и астронома Клавдия Птолемея. Он жил в первой половине II века н. э. и оставцл после себя сочинения в 13 томах под названием "Великое собрание, или Великое построение". Это была своего рода энциклопедия астрономических знаний того времени. До нас она дошла под греко-арабским названием "Альмагест".

В "Альмагесте" приведены результаты огромной вычислительной работы, проделанной Птолемеем. Они представлены в виде таблиц синусов и предназначались для облегчения труда астронома.

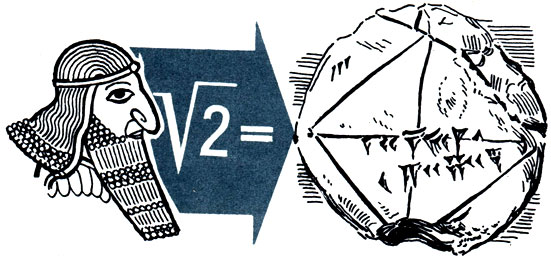
На вавилонском клинописном тексте представлен квадрат с диагональю. Сторона равна 30, что записано вверху слева. Около диагонали записано приближенное значение √2

По таблицам можно было определить синусы дуг до 90° через каждую четверть градуса, а по теореме Пифагора - вычислять любой элемент (сторону или угол) плоского прямоугольного треугольника, два других элемента которого известны.

Таблица Птолемея - первая из дошедших до нас тригонометрических таблиц.

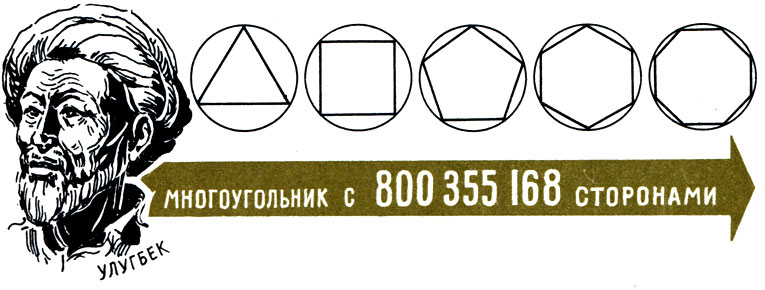
Выдающийся математик и астроном Улугбек вычислял с шестнадцатью знаками после запятой отношение длины окружности к радиусу, то есть число 2 π. Постепенно увеличивая число сторон правильного многоугольника и приближаясь к окружности, он дошел до многоугольника с 800355168 сторонами!

Длительный период римского господства в Европе не отмечен какими-либо выдающимися достижениями в математике. Только александрийский ученый Диофант, живший в III веке н. э., внес в алгебру новые своеобразные алгебраические уравнения.

Огромную роль Для техники вычислений сыграло изобретение логарифмов. Оно повлияло на всю методику решения математических задач. Привыкшим со школьной скамьи пользоваться таблицами логарифмов трудно даже представить себе изумление и восхищение, которое вызвало их появление.

Великий ученый П. С. Лаплас писал: "Изобретение логарифмов, сокращая вычисления нескольких месяцев в труд нескольких дней, словно удваивает жизнь астрономов".

Он говорил об астрономах потому, что сам был астрономом и в те времена им приходилось выполнять наиболее сложные и утомительные вычисления.

Слово "логарифм" греческое. Оно составлено из двух слов: "логос" - "отношение" и "аритмос" - "число". Таким образом, "логарифм" означает "число, измеряющее отношение".

На чем основаны удивительные свойства этих чисел, облегчающие вычислительный труд, те таблицы, которыми пользуетесь и вы на уроках математики?

Несколько простых примеров помогут вам в этом разобраться.

Возьмем какое-нибудь число, например 2, и составим таблицу чисел, полученных от его возведения в степень целых чисел:

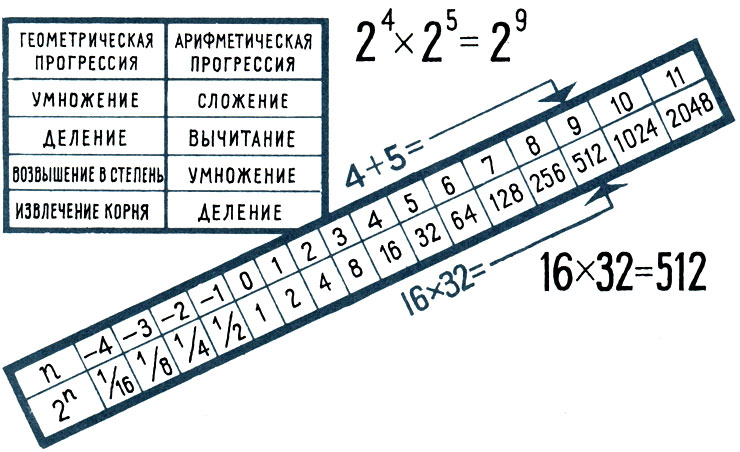
Вверху показано, что действиям над числами в геометрической прогрессии соответствуют более простые действия над ними в арифметической прогрессии

Верхняя строчка таблицы - арифметическая прогрессия с разностью, равной единице. Нижняя - геометрическая прогрессия со знаменателем 2. Этой таблицей можно уже пользоваться для упрощения вычислений.

Попробуем с ее помощью умножить 16X32. В верхней строке таблицы над этими числами стоят 4 и 5. Сложим их. Получим 9. А под девяткой в нижней строке, как видите, находится число 512. Это и будет искомый результат. Действительно, 16X32=512.

Почти так же можно найти частное от деления двух чисел, например 8 на 1/16. Но теперь нужно взять разность чисел, расположенных в таблице над ними. Она равна 7, так как 3 - (-4) после раскрытия скобок и сложения дадут 7. В нижней строчке этой разности найдем искомое частное: 128.

А такое сложное действие, как извлечение кубического корня из трехзначного числа, например из 512, делается с необыкновенной легкостью.

Судите сами. Взгляд на таблицу, и мы находим показатель степени для 512. Он равен 9. Теперь разделим его на степень кубического корня - на 3. И вот под частным, равным 3, тотчас же появится ответ - 8. Это и есть значение корня.

Наша таблица очень примитивна, но все же дает наглядное представление об общих свойствах членов арифметической и геометрической прогрессии. Они-то и могут быть использованы для упрощения вычислений. Каким образом?

Расстояние (S) и время (t) связаны логарифмической зависимостью. Она показана кривой Непера

Если попытаться объяснить это словами, то пришлось бы написать много скучных фраз. А вот рисунок наглядно показывает, что умножению и делению чисел в геометрической прогрессии соответствует в арифметической прогрессии сложение и вычитание. А возвышение в степень и извлечение корня заменяются умножением и делением.

Расположите все восемь действий, о которых мы говорим, по степени сложности, и ваша таблица превратится в удивительные ступеньки: сделал шаг - упрощение, сделал другой - совсем просто!

Само собой разумеется, что составленная нами таблица пригодна только для вычислений, связанных с целыми числами, да и то не с любыми.

Настоящие рабочие таблицы логарифмов для точных вычислений впервые составил Джон Не-пер. Над этой работой выдающийся шотландский математик трудился около 20 лет. О причинах, побудивших его к этому, Непер говорил:

"Я старался, насколько мог и умел, отделаться от трудности и скуки вычислений, докучность которых обычно отпугивает весьма многих от изучения математики".

Выдающееся значение работ Непера в том, что он раскрыл сущность логарифма как новой, до него неизвестной математической зависимости. Ее открытие имело для вычислительной математики столь же большое значение, как открытие тригонометрических функций.

Со времени гениального изобретения Непера прошло около 350 лет. Более 500 различных образцов таблиц логарифмов было создано с тех пор. Они прочно вошли в арсенал вычислительных средств и по сей день занимают почетное место как пособие, облегчающее человеку вычисления.

Миллионы специалистов пользуются в повседневной работе логарифмами, начиная от сверхточных - двадцати- и более значных - таблиц и кончая "деревянными логарифмами" - счетными линейками, незаменимым средством технических расчетов. Люди всегда жили и теперь живут в мире непрестанного движения. Все, что нас окружает, движется: меняются с течением времени взаимное расположение планет Солнечной системы, температура и давление воздуха, силы, действующие в машине, токи, протекающие в электрической цепи, состояние живой клетки.

В других процессах движение протекает с огромными скоростями и длится сотые, тысячные, иногда миллионные доли секунды. Стремительно падает давление воздуха в районе, к которому приближается циклон. С колоссальным ускорением движутся элементарные частицы в синхрофазо* троне: они за секунды пробегают космические расстояния.

И при исследовании подобных процессов - их называют динамическими - ученых прежде всего интересует, как они изменяются во времени.

Для анализа и расчета динамических процессов нужны математические методы, которые, подобно сверхскоростному киноаппарату, позволяют улавливать изменения, происшедшие за ничтожно малые промежутки времени.

Таким "киноаппаратом" вычислений явились методы дифференциального и интегрального исчисления - науки об изменяющихся величинах. Ее создали гениальные математики Г. Лейбниц, И. Ньютон, Л. Эйлер и их ученики и последователи.

Но одно дело исследовать явления, столь же закономерные, как смена дня и ночи, чередование времен года, и совершенно другое дело изучать процессы, подверженные воздействию различных случайных обстоятельств.

Монета, брошенная вверх, с неизбежностью падает на землю. Можно даже вычислить, через сколько секунд это произойдет.

Но никакие расчеты не могут предугадать, какой стороной она упадет - гербом или решеткой. Она может упасть и так и сяк, и это зависит от множества случайных обстоятельств.

Игры, основой которых является случайный исход, интересовали таких выдающихся математиков, как Б. Паскаль и П. Ферма. Зародилась новая отрасль человеческих знаний - теория вероятностей. Было доказано, что вероятность - величина, доступная измерению.

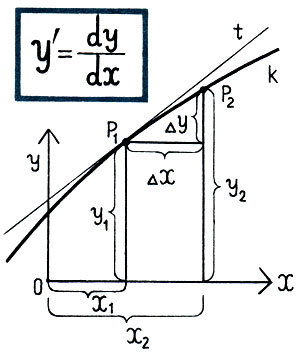
Изучение динамических процессов бывает связано с решением очень сложных дифференцальных уравнений

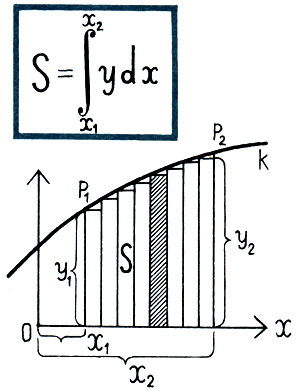
Математика уловила тот предельный переход, при котором ступеньки прямоугольников превращаются в плавную кривую. Она нашла предел, к которому стремится сумма (S) при бесконечном возрастании числа слагаемых, каждое из которых стремится к нулю. Этот предел называется интегралом функции.

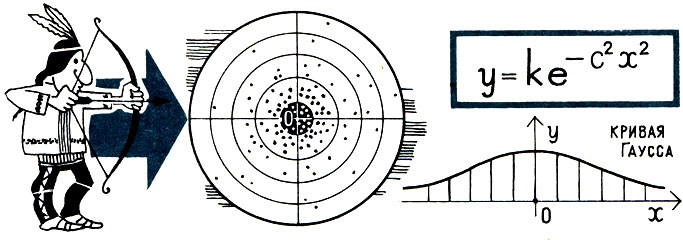
Математики сделали поразительное открытие: случайные величины подчиняются совсем не случайным закономерностям. Благодаря этому можно предвидеть среднюю точку попадания и заранее предсказать, в каких пределах будут находиться различные отклонения от средней величины

Но только в XIX веке трудами таких математиков, как К. Ф. Гаусс, П. Л. Чебышев, А. А. Марков, А. М. Ляпунов, теория вероятностей выросла в самостоятельную науку, в ту отрасль математики, которая получила в дальнейшем огромное практическое значение.

Немало времени затратили многие выдающиеся ученые на утомительные вычисления в поисках новых путей в математике и для проверки результатов своих вычислений.

Математики-вычислители не строят машин и зданий, в их кабинетах нет весов и колб, гальванометров и микроскопов, они не ставят опытов. Но математики вооружают машиностроителей и архитекторов, физиков и химиков, биологов и экономистов умением решать задачи, вооружают новейшими математическими методами.

Мы с вами - современники выхода вычислительной математики из колыбели. Родившись из запросов практики, она теперь сама влияет на развитие теории. Требует от теории новых эффективных методов, принципиально отличных от прежних.

Вычислительная математика сегодня разрабатывает правила численного расчета различных математических задач, оценивает сложность, трудоемкость и точность алгоритмов и методы их программирования на вычислительных машиеах. Эта работа чрезвычайно сложная. Есть алгоритмы, содержащие до миллиарда и более арифметических операций.

Вычислительная математика помогает не только традиционным своим подопечным - механике, физике, астрономии, - но и таким, казалось бы, далеким от нее разделам науки, как геология, медицина, лингвистика, экономика.

И здесь математики научились доводить решение задач "до числа".

Вычислительная математика разрослась вширь и вглубь. Она требует очень много специалистов. Крупнейшие математики считают, что уже теперь представляется возможным включить в программы средней школы элементы вычислительной математики и изучение устройства вычислительных машин.

"Они ждут вас, молодые, - говорит академик И. Виноградов, обращаясь к молодежи. - Вам прокладывать с ее помощью пути к далеким планетам и, возможно, к звездам, создавать с ее помощью машины, которые освободят творческие силы человека от черновой физической и умственной работы. Это дело ближайших десятилетий, и к нему надо быть готовым".

Добрая фея