Кибернетика в экономике

Кибернетика в экономике

Применение методов и средств
кибернетики - математических 
методов и электронных вычислительных
машин - при анализе экономики 
и выработке оптимальных (наилучших) 
решений для управления производством
и народным хозяйством. 

С формулами сквозь деньги и товары

Начнем этот рассказ с задачи. Завод, производящий партиями определенные детали, получает заказы на несколько месяцев раньше, чем надо их отправить заказчику. Завод может выполнять задание и в тот месяц, когда детали надо отправлять, и в более ранние сроки, если это по каким-то причинам выгодно заводу, а потом хранить их до срока. Но хранение деталей требует затрат. Вот и спрашивается, как организовать производство и хранение деталей, чтобы затраты на весь планируемый период были минимальными?

Не правда ли, сразу не решишь, как должен поступать при таких условиях завод.

Может быть, взять другую задачу - попробовать распределить детали для обработки на станках?

Оказывается, и это нелегко. Так, при распределении трех деталей по трем станкам количество вариантов распределения будет равно 108. Если распределять четыре детали между четырьмя станками, количество вариантов возрастет до 8272.

Эти примеры приведены здесь не случайно: подобного рода задачи приходится каждодневно решать экономистам, плановикам, диспетчерам, чтобы найти наилучший, или, как говорят, оптимальный, вариант в каждом конкретном случае.

Вот перед экономистом возникает обычный для него рабочий вопрос: как рационально распределить задания по выработке тканей между фабриками? Значит, он должен так спланировать использование ресурсов всех фабрик, чтобы они дали максимальное количество продукции,

причем ее себестоимость должна быть самой низкой, иными словами - план должен быть оптимальным.

План в данном случае должен отвечать на следующие вопросы:

Какие ткани, сколько и на каких станках нужно производить каждой фабрике?

Сколько всего разных тканей могут дать все фабрики? Какой при этом будет процент выполнения задания? Будет ли перевыполнение или недовыполнение?

Какова себестоимость тканей на отдельной фабрике и всех вместе?

От каких типов станков зависит выполнение задания?

Нужно ли вводить новые станки?

Чтобы решить задачу, потребовалось бы очень много времени, даже если бы мы распределяли три артикула тканей между тремя фабриками (вспомните пример с деталями и станками - 108 вариантов). Но чтобы все-таки выступить в роли плановиков, решим одну задачу подобного "профиля".

На три пристани привозят на баржах песок. Обозначим эти пристани I, II, III. Песок нужен для строительства четырех объектов. Назовем их А, Б, В, Г.

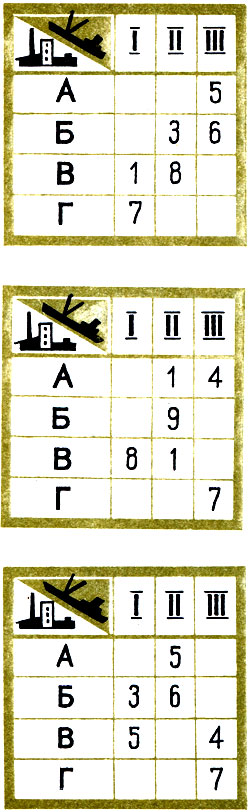
Чтобы решить эту задачу, нам понадобится сделать таблицы. Сначала обратимся к первой. В крайнем правом столбце дано нужное на день количество песка - 30 т. В нижней строке - пропускная способность каждой пристани. Объемы расхода и поставок сбалансированы. В клеточках указано, сколько километров между пристанями и строительством объектов.

Нам надо отыскать решение, которое бы так распределило песок с каждой пристани на каждую стройку, чтобы тонно-километры при автоперевозках были наименьшими.

Диспетчер автобазы распределил перевозки, как показано на второй таблице (в клеточках - количество песка с соответствующей пристани на соответствующие стройки). Все стройки при таком распределении получали нужное количество песка. А объем перевозок? Подсчитаем: 1X1+7X2+3X4+8X5+5x7+6x8= 150 тонно-километров.

Но бесспорно лучшим будет распределение, приведенное в третьей таблице. Здесь количество тонно-километров снижено в полтора раза: 8Х1+1Х2+9Х4+1Х5+4Х7+7Х3=100.

А вот и самый лучший, оптимальный вариант решения задачи, дающий объем перевозок в 1,7 раза меньше по сравнению с первым. Он записан в четвертой таблице.

Видите, сколько хлопот с решением "простой" экономической задачи, когда и задача конкретна, и вариантов мало, и цифры невелики.

Теперь все понимают, что даже семейный бюджет нелегко рассчитать на месяц-другой вперед с точностью хотя бы до рубля. Для предприятия же экономический расчет во сто крат сложнее. А подобные расчеты для группы предприятий, для какой-либо отрасли производства или же в масштабе всей страны?!

Попробуйте представить себе после этого всю масштабность экономических расчетов для такого народного хозяйства, каким является вся совокупность производства у нас в СССР!

Посмотрите, в какие цифры экономии "выливается" составление оптимального плана в пределах страны только по одной отрасли строительства. Оптимальный план размещения цементных заводов на территории нашего государства позволил сократить среднюю дальность перевозок с 565 км до 305 км. Это дало 140 миллионов рублей экономии в год. Кроме того, оказались ненужными намеченные к строительству неудобно расположенные заводы. Это позволило сэкономить еще 192 миллиона рублей. Подобного рода экономические задачи решают с помощью так называемого линейного программирования, разработанного советским ученым Л. В. Канторовичем.

Общую идею линейного программирования попытаемся пояснить на простом примере.

Организму человека для нормальной жизнедеятельности надо получать ежедневно определенное количество питательных веществ: жиров, белков, углеводов, витаминов, минеральных солей и т. д. Эти нормы по 15 видам питательных веществ установлены медицинской наукой на основе всесторонних исследований. Необходимые организму питательные вещества содержатся в тех или иных количествах в различных продуктах: хлебе, молоке, рыбе, овощах, фруктах, крупах - таких групп можно насчитать 40-50.

Возникает естественный вопрос: каким должен быть набор продуктов питания, чтобы полностью удовлетворять физиологическим потребностям организма и вместе с тем быть минимальным по цене? Речь, таким образом, идет о самом дешевом и в то же время полноценном, с медицинской точки зрения, питании.

Итак, надо выбрать из 50 групп продуктов питания набор, содержащий требуемые для организма 15 питательных веществ. Критерий оптимальности - цена набора. Она должна быть минимальной. На языке математики это означает, что нужно решить систему из 15 уравнений с 50 неизвестными!

Такие системы, где число неизвестных больше, чем число уравнений, имеют бесконечное множество решений. А нужно выбрать одно - наилучшее!

Для нашего примера можно ограничиться более скромной задачей: всего только двумя продуктами питания - хлебом и молоком и двумя видами питательных веществ - белками и кальцием.

Вот небольшая табличка, в которой указано, сколько белка и кальция содержится в килограмме хлеба и литре молока.

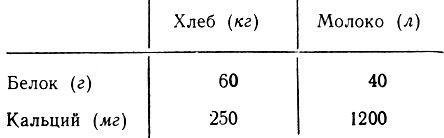
Таблица

Организм должен получать в день не меньше 100 г белка и 700 мг кальция.

Теперь надо вспомнить системы алгебраических уравнений.

Обозначим искомое количество хлеба в наборе через x₁, а количество молока через х₂. Коэффициенты а₁ и в₁ в первом уравнении - это, соответственно, содержание белка в килограмме хлеба и литре молока, а коэффициенты а₂ и в₂ второго уравнения - содержание кальция в тех же продуктах.

Мы знаем: чем больше хлеба и молока в наборе, тем пропорционально больше содержится в нем питательных веществ. Следовательно, зависимость здесь линейная, и мы снова имеем дело с системой линейных уравнений. Вот как она теперь выглядит:

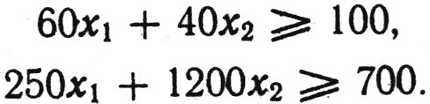
Знак ≥ означает "больше или равно". Здесь он имеет принципиальное значение. Если бы количества белка и кальция были строго регламентированы (в точности 100 г и 700 мг - ни больше и ни меньше), тогда в нашем примере все было бы ясно.

Два уравнения, две неизвестные величины. Такая система уравнений имеет единственное решение, и ни о каком оптимальном выборе не может быть речи. Все дело, однако, в том, что по условиям задачи организм может получать в день больше, чем 100 г белка и 700 мг кальция. А это дает возможность широкого выбора. Число возможных вариантов становится неограниченным.

Между прочим, в этом нетрудно убедиться. Написанные выражения очень просто превратить в равенство. Нужно только в каждое условие ввести еще по одной неизвестной величине, которая выравнивала бы его:

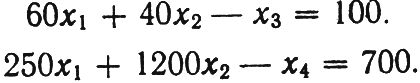
Вот мы и получили систему из двух уравнений с четырьмя неизвестными. Здесь может быть бесконечное множество решений - в зависимости от того, какое значение мы будем давать переменным х₃ и х₄.

Остается лишь добавить, что по вполне понятным причинам из всего многообразия возможных решений нас интересуют лишь такие, где x₁ и х₂ имеют неотрицательные значения - хлеб и молоко отрицательными быть не могут.

Допустим, килограмм белого хлеба стоит 21 коп., а литр молока - 28 коп. Следовательно, стоимость набора из х₁ килограммов хлеба и х₂ литров молока равна:

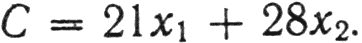
Это математическое выражение в линейном программировании называют целевой функцией. Она дает точную количественную характеристику цели, которую мы ставим перед собой, планируя нашу деятельность. Функция определяет тот критерий, с помощью которого мы сравниваем различные варианты плана, выбирая оптимальный.

И в нашей задаче четко выраженная целевая функция обеспечит выбор оптимального набора продуктов питания - самого дешевого. Это такие неотрицательные значения переменных х₁ и х₂, которые удовлетворяют условиям задачи (написанной системе уравнений) и при которых целевая функция имеет минимальное из всех возможных значений.

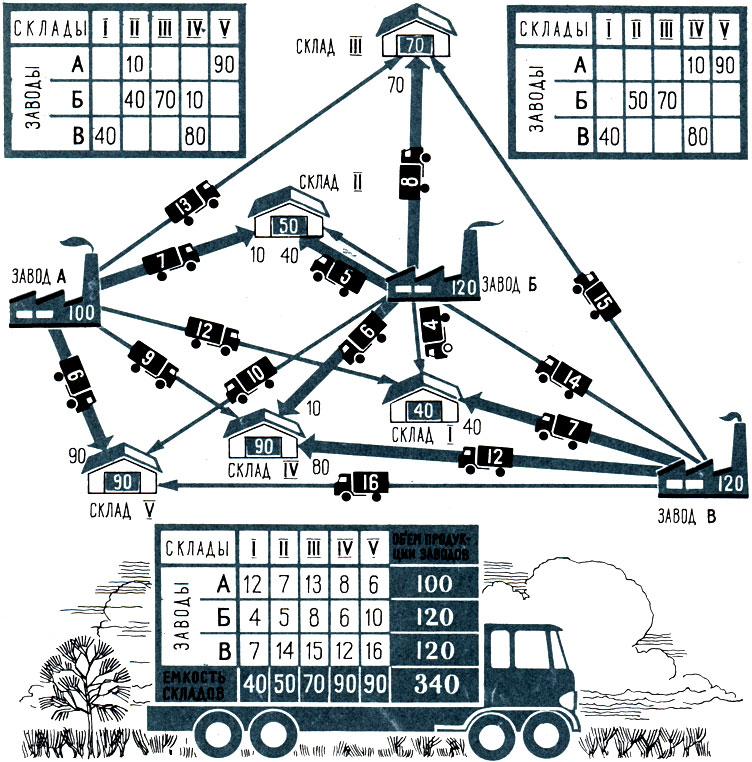
Исследование транспортных операций линейным программированием. Надо получить минимальную стоимость перевозок, принимая во внимание объем продукции каждого завода, емкость каждого склада и стоимость транспортирования единицы товара с каждого завода на каждый склад. Вверху слева и справа показаны два оптимальных - наилучших - решения. В клетках таблиц обозначено, какое количество товара на какой склад выгоднее возить. Внизу в таблице - стоимость перевозки груза с завода на склад. В центре - на схеме маршрутов перевозок - стоимость указана на грузовиках. Жирными стрелками обозначен наивыгоднейший путь

Методы линейного программирования как раз и предназначены для решения такого типа задач.

В электронную машину вводят условия задачи в виде системы уравнений и неравенств и формулу целевой функции. Машина выбирает какой-нибудь начальный вариант и анализирует его. Анализ тотчас же обнаруживает, является ли этот почти наугад выбранный вариант оптимальным. Само собой разумеется, такой случай почти невероятен. Если вариант, не оптимальный, анализ указывает, как выбрать следующий, который наверняка лучше начального - для него целевая функция будет меньше.

Новый вариант опять анализируется - проверяется на оптимальность, и в случае отрицательного ответа переходят к следующему, еще лучшему варианту. И так шаг за шагом идет поиск, пока анализ не покажет: найденное решение оптимально - варианта с меньшей целевой функцией не существует.

Как видите, в основе метода лежит не слепой перебор всех возможных вариантов, а разумный поиск, где каждый шаг приближает к цели. И когда она достигнута - машина выдала оптимальный вариант,- можно с полной уверенностью утверждать, что лучшего при заданных условиях задачи нет, это гарантируют методы линейного программирования.

При высоких темпах развития народного хозяйства непрерывно ускоряется взаимодействие всех его частей, динамичней становятся экономические показатели. В таких условиях очень важно вести непрерывное планирование и оперативно управлять всеми звеньями народного хозяйства. Малейшее запаздывание в планировании и управлении вызывает не меньшие потери, чем неточность планирования.

Свыше двух миллионов человек были заняты до недавнего времени у нас в стране управленческим трудом. Вероятно, мало кто знает, что только на одном Горьковском автозаводе снабжением завода необходимым сырьем и сбытом готовой продукции занималась целая армия работников - свыше пяти тысяч человек!

Тем, кто управляет производством, в год приходится обрабатывать миллиарды документов. Сегодня люди, вооруженные счетами и арифмометрами, уже не в состоянии справиться с потоками информации. Очень трудно с такими техническими средствами рассчитать множество вариантов планов и, опираясь на точную информацию, обеспечить оптимальность управления народным хозяйством.

В Институте кибернетики Украинской Академии наук подсчитали, что количество планово-экономической информации растет пропорционально квадрату роста объема производства. Значит, через 20 лет больше половины населения Советского Союза должно будет заниматься управленческой работой. Не случайно экономисты мечтают о том дне, когда не только счеты, но и арифмометры будут сданы в музей, а на смену им придет полная автоматизация планово-экономических расчетов.

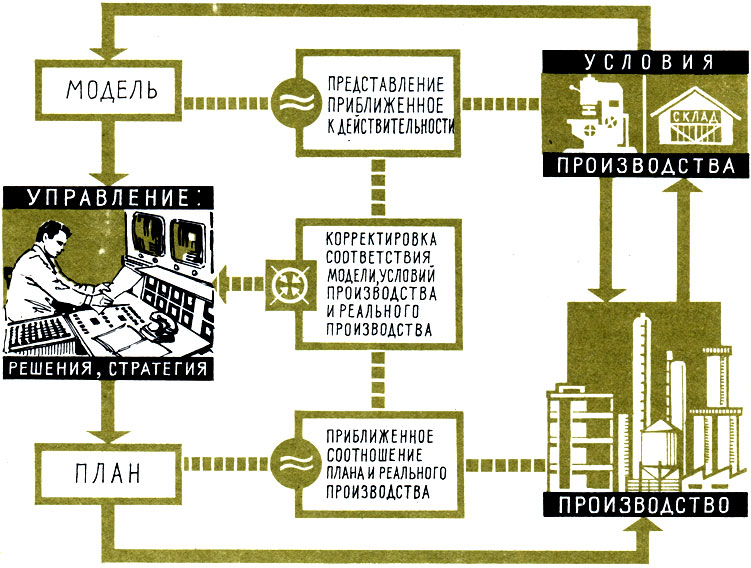
Схема управления производством

Математические методы можно образно назвать золотым ключом для открывания дверей в таинственное царство экономики.

Конечно, решение экономических задач - дело чрезвычайно трудное. Практика показывает, что чем выше уровень производительных сил в стране, тем более усложняется руководство хозяйством. Количество и сложность расчетов постоянно увеличиваются: ведь увеличивается объем продукции, убыстряются темпы роста, разделяются отрасли народного хозяйства, расширяются внутрихозяйственные связи.

Поэтому широким фронтом ведутся работы по использованию "электронных арифмометров" в планировании народного хозяйства областей, республик и всего Советского Союза.

В Белоруссии, например, с помощью машин был рассчитан и внедрен наивыгоднейший план перевозки леса. А в Ленинграде составили планы речных и морских перевозок по основным речным и морским бассейнам. Вычислительный центр Госплана СССР рассчитал, как лучше закрепить поставщиков за потребителями листового проката. В Туркмении уже на протяжении нескольких лет значительная часть расчетов по отраслям народного хозяйства ведется на машинах.

Таких примеров можно привести очень много. Не случайно известный специалист в области кибернетики академик В. М. Глушков утверждает, что скоро "автоматизированные системы станут столь же необходимым инструментом научного исследования экономистов, как синхрофазотрон для физиков или электронный микроскоп для биологов".

Использование электронно-вычислительных машин не только ускоряет расчеты, но и в десятки, в сотни раз уменьшает время, нужное для разработки планов. Электронные машины, используемые для экономических операций, позволяют централизованно управлять производством.

При управлении народным хозяйством проявляется своеобразная иерархичность "электронно-вычислительных экономистов". На первом "этаже" стоят "низовые ячейки" по сбору, хранению и переработке информации. Они позволяют планировать работу участков, цехов, предприятия в целом, позволяют ежедневно видеть состояние производства.

Дальше идут периферийные установки для переработки и хранения информации. Это электронные машины, соединенные каналами связи с центральными "фабриками чисел" экономических районов или отраслей производства или других объединений.

Еще дальше - в центре - система получения, обработки и хранения информации должна давать полное представление о положении дел в каждой конкретной отрасли и в целом.

Специалисты считают, что создание всесоюзной сети по сбору, хранению, переработке и передаче экономической информации трудно переоценить, значение ее необычайно велико.

В социалистическом плановом обществе необходимо стремиться к наилучшим показателям, к так называемому оптимуму отдельно в каждой отрасли и к оптимуму в целом во всем народном хозяйстве. Именно об этом говорил В. И. Ленин, указывая, что "...только то строительство может заслужить название социалистического, которое будет производиться по крупному общему плану, стремясь равномерно использовать экономические и хозяйственные ценности".

В. И. Ленин неоднократно обращал внимание и на научную организацию управленческого труда, без которого невозможно правильное руководство народным хозяйством. Он писал, что люди, пришедшие работать в управленческом аппарате, "...должны выдержать испытание на знание основ теории по вопросу о нашем госаппарате, на знание основ науки управления".

Теперь бесспорно существенной частью научного управления являются математические методы. Теперь без них не мыслится экономическое планирование производства, науки, техники, распределение ресурсов; обеспечение рабочей силой; непосредственное, конкретное руководство, управление и контроль на предприятии.

Надо было найти лучший вариант развития угольных предприятий

Таким будет Всесоюзный центр по сбору, хранению, переработке и передаче экономической информации

Кузбасса на 1962-1970 годы. При этом следовало учесть число шахт, марки углей, затраты труда и сотни других обстоятельств. В Кузбассе около 100 шахт и разрезов, по ним предусмотрено примерно 200 вариантов развития. Методами математического планирования был найден оптимальный вариант решения такой сложной задачи. Оказалось, развитие шахт Кузбасса требует на 200 миллионов рублей капитальных затрат меньше, чем план, составленный обычным путем.

План машины оказался на 43% экономичнее плана человека!

Теперь уже отказываются от экспериментов "в натуре", от дорогостоящих поисков с помощью "проб и ошибок" и все чаще прибегают к моделированию. Так была решена грандиозная задача - разработана научная модель пятилетнего плана развития народного хозяйства СССР на 1971 -1975 годы. Даны практические рекомендации по улучшению пропорций развития народного хозяйства и его отраслей, рациональному использованию материальных и трудовых ресурсов; вопросам хозяйственной реформы.

Новый метод позволяет прогнозировать научно-технический прогресс в связи с экономикой, оценивать природные ресурсы, определять оптимальные размеры государственных резервов, оптимизировать и самую структуру органов планирования.

В заключение, чтобы показать всю серьезность и важность применения кибернетики в экономике, сошлемся на составление баланса народного хозяйства страны - важнейшей части социалистического планирования.

Баланс - это система экономических показателей, характеризующих основные соотношения, пропорции и темпы производства, источники и резервы увеличения национального богатства страны, повышение благосостояния народа.

Математические методы позволяют с большой степенью точности выявить все пропорции и связи в народном хозяйстве, изучить его эффективность. Короче говоря, мы более быстро и более точно теперь можем понять, правильно ли используется все наше народное богатство. А оно очень велико: например, совокупность общественного продукта Страны Советов в 1968 году оценивалась в 500 миллиардов рублей!

С формулами сквозь деньги и товары