Логика математическая

Логика математическая

Наука, изучающая формы рассуждений 
и доказательств математическими методами. 

Три богатыря

Кто из школьников не знает, что такое алгебра? В школе изучают задачи на решение алгебраических уравнений. Пишут алгебраические выражения, составленные из" букв и цифр, соединенных знаками действий: сложения, вычитания, умножения, деления.

А не задумывались вы над тем, что раз в алгебре действия производятся над символами-буквами, может быть, существует и алгебра языка - алгебра, с помощью которой можно было вычислять ответ на вопрос так же, как вычисляют ответ на задачу?

Великий древнегреческий мыслитель Аристотель, живший в IV веке до н. э., создал науку логику - науку правильно рассуждать, науку о формах и законах мышления. Он подверг анализу человеческое мышление, такие его формы, как понятие, суждение, умозаключение, и рассмотрел мышление со стороны строения, структуры, то есть с формальной стороны. Так возникла формальная логика - наука, пытавшаяся найти ответ на вопрос, как мы рассуждаем, изучающая логические операции и правила мышления.

Эти попытки привели в средние века к мысли находить всевозможные истины с помощью простого комбинирования общих понятий. Для этой цели даже строили "мыслительные машины". Средневековые философы мечтали с их помощью разрешить все проблемы науки, все загадки жизни, все тайны Земли и Неба.

"Мыслительная" машина средневекового философа, богослова и алхимика Раймунда Луллия была устроена очень просто. На большом неподвижном круге по окружности были написаны девять вопросов: "Сколько?", "Который из двух?", "Когда?", "Где?", "Какого качества?" и другие, подобные этим.

Внутри круга один над другим были расположены еще пять кругов уменьшающегося диаметра. Они могли вращаться независимо друг от друга. Каждый круг делился на девять секторов-"камер". В них были сделаны надписи. В одном круге названия девяти главных грехов и добродетелей, в другом - девяти главных физических свойств.

Луллия вместил в камеры всю известную ему премудрость. Вращая те или иные круги, он передвигал их на одно, два, три деления. При этом неподвижным был то первый, то второй, то первый и третий или пятый и второй. И всякий раз против вопросов главного неподвижного круга оказывались различные сочетания слов.

Ясно, что подобная машина не могла решать никаких логических задач. Ее "откровения" больше всего походили на бессмыслицу. Иначе и быть не могло. Изобретатель Раймунд Луллия хотя и называл свое детище "великим искусством", но он не имел понятия о законах математической логики, на которых основана работа современных логических машин.

Основоположником математической логики считают великого немецкого математика и философа Готфрида Вильгельма Лейбница. Это он в XVII веке попытался построить первые логические исчисления, арифметические и буквенно-алгебраические. Он сблизил логику с исчислением, усовершенствовал и уточнил логическую символику.

На фундаменте, заложенном Лейбницем, другой великий математик, Джордж Буль, отец писательницы Э. Войнич, автора романа "Овод", воздвиг здание новой области науки - математической логики. Он вывел для логических построений особую алгебру. В отличие от обычной, в ней символами обозначают не числа, а высказывания.

Когда дети только начинают считать, они, например, научившись складывать два яблока и три яблока, становятся в тупик, когда надо сложить три дома и два дома. Но затем в школе ребята усваивают, что существуют числа вообще, а не какое-то число яблок, домов, вагонов и т. д. Изучая алгебру, ребята постигают, что понятие а2 значительно шире, чем 13 яблок, взятые 13 раз.

То же и в математической логике: надо абстрагироваться от содержания высказываний. Оно для математической логики не имеет значения, так же как для алгебры безразлично, что стоит за обозначением х - количество рыб, автомобилей или звезд.

Коль скоро мы в этой логике имеем дело с математикой, для нее не важен конкретный смысл суждения. Для нее важно только одно - истинно данное высказывание или ложно.

Следует обратить внимание и на такое обстоятельство. Оказывается, каждый из нас, можно сказать, только тем и занимается, что обращается к формальной логике. Мы бессознательно - особенно отстаивая свою точку зрения - приноравливаемся к законам алгебры языка, ибо (по мнению специалистов) математическая логика как бы "образует основную ткань нашего мышления". На ней - конечно, в самом широком смысле - базируются общие свойства высказываний, основы рассуждений.

Представьте себе, что вас спросили: почему днем бывает светло? А вы ответили: потому что днем свет делает день светлым. Вы нарушили правила логики, логику рассуждений: вы ничего не объяснили. Еще Мольер увековечил в бессмертной комедии "Мнимый больной" такой бездоказательный метод мышления. В пьесе бакалавру на экзаменах ставится вопрос: "Почему опиум вызывает сон?" Бакалавр отвечает: "Потому, что в нем содержится снотворная сила, которая имеет способность усыплять чувства".

Как видим, здесь слова обычного языка, взятые вместе в контексте, не дают ясного, точного смысла.

Еще в древности было известно рассуждение, ставшее классическим образцом логического доказательства: "Все люди смертны. Сократ человек. Следовательно, Сократ смертен".

Чтобы придать точное значение словам, ученые придумали специальные однозначные символы. Такая символика позволяет выявить логическую структуру мысли или рассуждения. Точные значения слов позволили вычислять связи между символами слов, отношения между ними. То, что раньше трудно было выразить словами обычного языка, теперь с большой легкостью можно представить символами математической логики.

Вот простой пример. Н₂0 - обозначение для воды. Оно указывает на присутствие двух атомов водорода и одного атома кислорода на каждую молекулу соединения. В этой записи факты относятся к химии, числа - к математике, а обозначения -- к символической логике.

Давайте постепенно подойдем к рассмотрению ее законов.

Логика рассматривает три различные формы, в которых осуществляется мышление: понятие, суждение и умозаключение.

"Этот вписанный угол, опирающийся на диаметр", - это есть понятие; если мы говорим не о всех углах, то понятие единичное. А "все вписанные углы, опирающиеся на диаметр, прямые" - уже суждение, поскольку в нем об объекте суждения высказывается, каковы его свойства.

Если из двух суждений выводится третье, то этот процесс называется умозаключением. Его основной вид в логике называется силлогизмом. В силлогизме одно из суждений - общее - названо большой посылкой, другое суждение - частное - малой посылкой, заключительное суждение - вывод.

Возьмем суждение "все вычислительные машины облегчают труд человека" в качестве большой посылки. А суждение "арифмометр - вычислительная машина" - в качестве малой. Тогда вывод из этих суждений будет: "арифмометр облегчает труд человека".

Суждения могут быть истинными или ложными. Если суждения истинны, то при соблюдении определенных законов образования силлогизма мы всегда получим правильный вывод - истинное заключение о суждении, как наш вывод об арифмометре.

Но если при соблюдении правил образования силлогизма мы получаем неверный, ложный вывод, то это значит, что по крайней мере одна из посылок неверна.

Наоборот, если все посылки были истинными суждениями, но в результате умозаключения был получен ложный вывод, это означает, что нарушено какое-то правило образования силлогизма. Нелепый вывод "все ученики двоечники" получится у нас из-за неправильного построения силлогизма "Петров - двоечник. Петров - ученик".

Оказывается, так же как и для математической задачи, решение любой логической задачи имеет свою "технологию". Она составляется из простейших операций, похожих на сложение и умножение. Их выполняют по специальным правилам. С их помощью каждый может решить сложную логическую задачу. То же самое может сделать и автоматическая машина.

Для машины логическую задачу надо представить в виде формул.

Обычное дело - облечь в уравнения количественные закономерности, выраженные в числах. Но как заковать в формулы свободные логические суждения? Суждения, высказанные словами? Каким образом, например, можно изобразить в виде формул суждение: "Я обязательно поеду на футбольный матч, если достану билет или меня пригласит товарищ и если не будет дождя"?

Оказывается, можно. Но для объяснения придется привести некоторые логические рассуждения.

В рассуждении, сделанном любителем футбола, его поездка на стадион оговорена несколькими условиями. Вот они:

1. Я достану билет.

2. Меня пригласит товарищ.

3. Будет дождь.

Простые высказывания могут быть связаны между собой словами ИЛИ, И, НЕ. Причем сложные высказывания всегда выражаются через простые с помощью этих слов. Они, подобно трем богатырям, все могут в логике.

Можно условиться каждое из этих слов обозначать для краткости каким-либо символом, как в математике вместо слова "плюс", "минус", "умножение", "деление" пользуются соответствующими знаками.

Обычно слово ИЛИ принято обозначать крестиком ( + ), а слово И - знаком умножения: точкой (^.).

Теперь остается каждое высказывание обозначить для сокращения какой-либо буквой. А его отрицание, то есть слово НЕ, обозначать той же буквой, но с черточкой наверху.

Например:

Я достану билет - Б. Я не достану билета -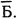

Меня пригласит приятель - П. Меня не пригласит приятель -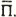

Будет дождь - Д. Не будет дождя -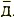

Теперь запишем с помощью этих символов сложное высказывание: "Я достану билет, и не будет дождя, или меня пригласит приятель, и не будет дождя".

Вот эта запись:

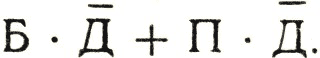
Как и в алгебре, общий множитель можно вынести за скобку. Формула будет тогда в таком виде:

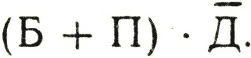
Читается она так: "Я достану билет, или меня пригласит приятель, и не будет дождя".

В заявлении нашего любителя футбола это сложное высказывание равносильно условию поездки на матч, которую мы обозначим буквой М. Теперь заявление можно записать очень краткой формулой:

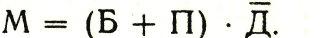
Вы знаете, что всякое логическое суждение может быть либо истинным, либо ложным. В математической логике условились истинное высказывание обозначать единицей, а ложное нулем. Опять 1 и 0.

"Я выучила все уроки", - заявила ученица своему классному руководителю. Обозначим это заявление для краткости буквой У. И если высказывание ученицы истинно, то У=1. Значит, если У=1, то 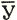=0, так как в данном случае высказывание "я не выучила уроков" было бы ложным.

И наоборот, если бы ученик не выучил уроки, то У=0, и тогда 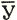=1.

Это правило является в логике общим. Если какое-либо высказывание В=1, то 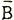=0, и наоборот: если В=0, то 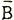=1.

Нам остается еще познакомиться с несколькими положениями математической логики, и тогда мы будем знать основные ее законы.

Ясно, что В+В=В и ВВ=В.

Действительно, сложное высказывание "я иду гулять или я иду гулять" ничем не отличается от простого высказывания "я иду гулять". Точно так же "приемник будет работать и приемник будет работать" равносильно простому высказыванию "приемник будет работать".

Столь же очевидны следующие два положения:

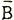В+=1 и В*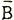= 0.

В самом деле, сложное высказывание "дождь будет или дождя не будет" истинно в том или другом случае - оно всегда истинно. Такого рода прогноз погоды всегда был бы правильным, хотя вряд ли кого-либо устроил.

А сложное высказывание "телевизор включен и телевизор не включен" всегда ложно. Соединение с помощью И двух противоположных суждений никогда не может быть истинным.

Теперь, когда мы логику претворили в формулы, зададим себе такой вопрос: можно ли "вычислить" истину? Оказывается, можно.

Есть такая книжка "Математическая смекалка" - сборник миниатюр для гимнастики ума. Каких только затейливых задач, математических игр и фокусов там нет! В главе "Математика почти без вычислений" даны задачи, для решения которых требуется построить цепочку искусных и тонких рассуждений. Одна из задач, "Уголовная история", очень подходит для иллюстрации рассказа о математической логике. Вот эта задача в несколько измененном применительно к этой книге виде.

Неприятная история. В одном из классов школы разбито окно. Выбить стекло мог только кто-нибудь из четырех учеников: Леня, Дима, Толя и Миша.

При опросе учеников каждый из них дал по три показания.

Леня. 1. Я не виноват. 2. Я даже не подходил к окну. 3. Миша знает, кто это сделал.

Дима. 1. Стекло разбил не я. 2. С Мишей я не был знаком до поступления в школу. 3. Это сделал Толя.

Толя. 1. Я не виновен. 2. Это сделал Миша. 3. Дима говорит неправду, утверждая, что я разбил стекло.

Миша. 1. Я не виноват. 2. Стекло разбил Леня. 3. Дима может поручиться за меня, так как знает меня со дня рождения.

При дальнейших расспросах каждый ученик заявил, что сделал два верных заявления и одно ложное.

Попробуем с помощью математической логики найти виновного.

Нам известно, что сложное высказывание каждого из них, когда оно истинно, равно единице, когда ложно - нулю.

Значит, высказывание каждого из ребят будет истинным, когда верно первое и второе и неверно третье показание, или верно первое и третье и неверно второе, или верно второе и третье и неверно первое.

Каждого из учеников обозначим буквой его имени с цифрой показания внизу. Запись будет выглядеть так:

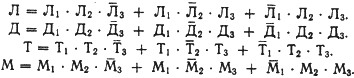
Если внимательно проследить показания учеников, то легко заметить, что первое и третье показания Толи равносильны. Действительно, утверждение "Я не виновен" и "Дима говорит неправду, утверждая, что я разбил стекло" по существу одно и то же. Тогда Т₃=Т₁, а T₃=T₁. Заявление Толи теперь можно записать так:

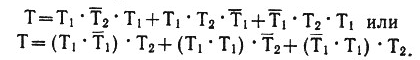
Но мы знаем уже, что противоречивые высказывания дают ложь. Поэтому (T₁*T₁)=0. А если один из сомножителей равен нулю, то заявление Толи примет такой вид: T=T₁*T₁*T₂ = T₁*T₂. Оно будет истинным, равным единице, если каждый .из сомножителей равен единице. Следовательно:

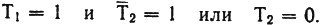
Таким образом, мы нашли, что первое высказывание Толи верно, а второе ложно. А так как он сказал: 1. Я не виноват. 2. Это сделал Миша. 3. Дима говорит неправду, утверждая, что я разбил стекло, - то ясно, что стекло разбили не Толя и не Миша.

Но теперь ясно и то, что третье показание Димы, в котором он обвиняет Толю, ложно. Значит, Д₃=0 и Д₃=1. Раз так, то в заявлении Димы, записанном в виде формул, последние два слагаемых обратятся в нуль, и формула примет простой вид:

А мы уже нашли, что 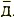₃=1, следовательно, Д₁=1 и Д₂=1.

Первое и третье показания Димы верны. Выходит, он не виновен.

Третье показание Миши противоположно второму показанию Димы. Запишем: М₃=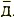₂. Значит, М₃=0, а 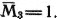Заявление Миши теперь выглядит так:

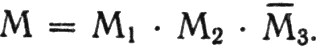
Оно истинно только в том случае, когда M_l=1, М₂=1,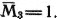

Второе показание Миши истинно! Стекло разбил Леня.

Так формулы математической логики быстро и безошибочно помогли найти виновника.

Математическая логика с развитием вычислительных машин оказалась в тесной взаимосвязи с вычислительной математикой, со всеми вопросами конструирования и программирования электронных счетных машин.

Все началось с того, что ученые сперва предположили возможность построения электрических схем на базе математической логики. Затем построили такие схемы. А теперь всевозможные электронные схемы лежат в основе вычислительных машин.

Смотрите. Если условиться записывать контакты, замыкающие цепь от сигналов а и в, теми же буквами а и в, а контакты, размыкающие цепь при наличии этих сигналов, - символами а¹ и в¹, и если условиться параллельное и последовательное соединения контактов обозначать знаками сложения и умножения, то операции а¹, а+в, ав производятся соответственно по правилам логического отрицания (НЕ), сложения (ИЛИ) или логического умножения (И). Замкнутая цепь при этом - 1 (истина), а разомкнутая - 0 (ложь).

Представьте себе электрическую схему, например цепь из источника тока, звонка и двух выключателей. В такой цепи, чтобы зазвонил звонок, то есть чтобы прошел сигнал, надо включить И первый, И второй выключатели. Подобная схема называется схемой совпадения, или логической схемой И. В ней только при совпадении во времени обоих сигналов на выходе появляется импульс.

В другой схеме выключатели- соединим параллельно. Теперь надо включить ИЛИ первый, ИЛИ второй выключатели, и тогда звонок зазвонит. Такая схема называется схемой разделения. Она осуществляет логическую операцию ИЛИ. Схема позволяет в одну точку подать напряжение от различных линий без замыкания их между собой.

Схему отрицания, или логическую схему НЕ, можно назвать цепью наоборот. В ней один вход и один выход. Но импульс тока на выходе появляется лишь тогда, когда на входе нет сигнала.

Конечно, бессмысленно ставить в электронных быстродействующих машинах электрические цепи с выключателями. Здесь работают электронные устройства. Они воспроизводят те же логические операции, но с огромной скоростью.

Вот, например, три электронно-ламповые схемы. Первая - НЕ, вторая - И, третья - ИЛИ. Как они работают?

Воспользуемся аналогией между электрическим током и водотоком. Посмотрите, как падает уровень воды в сосудах, и вам все станет ясно.

Если НЕ сдвигать задвижку, уровень воды в сосуде упадет.

Если сдвинуть И первую, И вторую задвижки, уровень воды в сосуде упадет.

Если сдвинуть ИЛИ первую, ИЛИ вторую задвижки, уровень воды в сосуде упадет.

В электронных лампах происходит примерно то же самое. Только течет не вода, а электрический ток. Вместо уровней воды - величины напряжений на выходе. Схемами же управляют не задвижки, а импульсы тока.

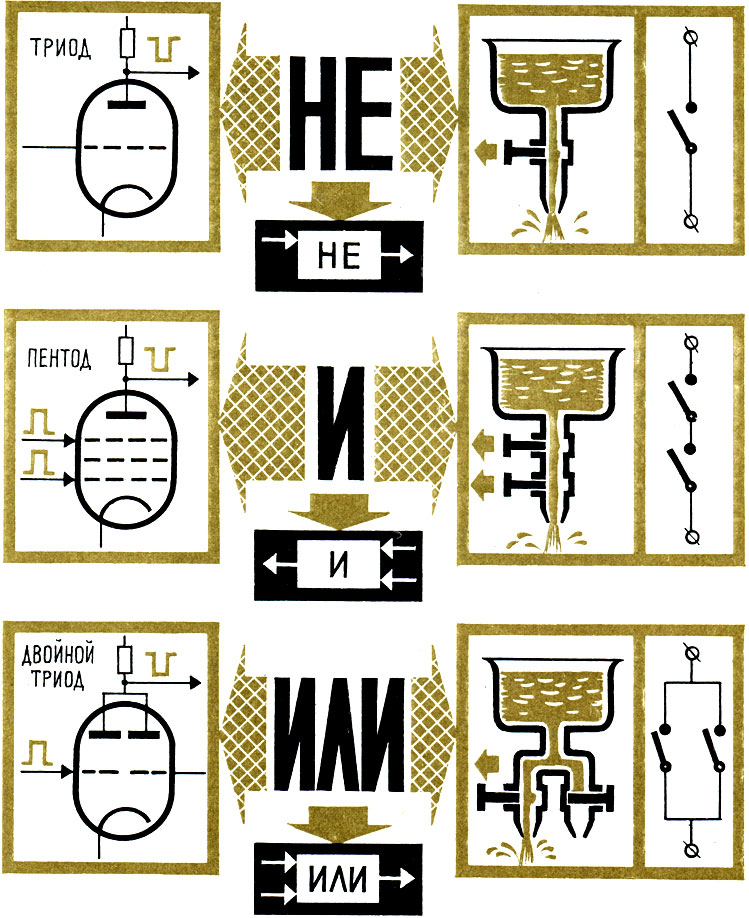
НЕ, И, ИЛИ в электронных схемах и их аналогии

Вот мы и получили, так сказать, овеществленные, материализованные в проводах и лампах схемы, реализующие три основные логические операции: наши всемогущие И, ИЛИ, НЕ. Они-то и помогают машине "рассуждать" во время работы: И - соединять, ИЛИ - выбирать, НЕ - отрицать.

Если вспомнить, что триггер, показывая единицу и нуль, тем самым будто говорит "да" или "нет", то станет ясно, что "язык" машин, несмотря на свою бедность, позволяет кодировать все числа, слова, вести логические рассуждения.

Применение исчисления высказываний в автоматах, в электронных схемах и связывает математическую логику с кибернетикой, заставляет эту "сугубо кабинетную" науку, науку абстрактную, приносить практически ощутимые результаты. Грубо говоря, математическая логика работает везде, где и над чем работают электронно-вычислительные машины. Ведь каждая задача в машинах решается по ее непреложным законам.

Но это только одна сторона дела. Другая - в том, что и сами схемы вычислительных машин, будь то электронные лампы, полупроводники и другие элементы, анализируются и разрабатываются с помощью математической логики.

Три богатыря

порево ebalka.tv