Энтропия

Энтропия

В теории информации это мера 
неопределенности ситуации (случайная величина). 

"Демон" открывает двери

Приготовьтесь сразу к тому, что вам придется запастись терпением. Да, да. Чтобы разобраться в вопросе об энтропии, понадобится прежде всего терпение, потому что не сразу вы уловите все оттенки и "цвета" нового понятия. И не удивляйтесь такому положению: ученые еще по многим деталям в вопросах об энтропии не пришли к полному согласию, к тому состоянию, которое называется единомыслием.

Вот высказывания видных ученых, признанных авторитетом в данном вопросе, пробующих с разных точек зрения рассказать простыми "человеческими" словами, что же за орешек они пытаются раскусить.

"Реальная ценность понятия энтропии определяется в первую очередь тем, что выражаемая им "степень неопределенности" опытов сказывается во многих случаях именно той характеристикой, которая играет роль в разнообразных процессах, встречающихся в природе и технике и так или иначе связанных с передачей или хранением каких-либо сообщений". Это одно утверждение.

А теперь обратите внимание на другое:

"Чтобы понять, что такое энтропия в теории информации, лучше выкинуть из головы все, что хоть как-нибудь связано с понятием энтропия, применяемым в физике".

О трудностях понятия энтропии и проблемы энтропии (и в физике, и в теории информации) говорит третье высказывание:

"Движение в этих областях напоминает движение в джунглях, полных ловушек. Наиболее знакомые с этим предметом обычно наиболее осторожны в разговорах о нем".

Обратим внимание: ученые в один голос подчеркивают неразрывную связь энтропии с теорией информации. А это очень важно, ибо теория информации признана мощным средством исследования и служит самым надежным проводником в блужданиях по сложнейшим лабиринтам во многих современных науках.

Это своего рода присказка, вводящая нас в курс дела, а сказка - что такое энтропия - впереди.

Слово "энтропия" впервые употребил немецкий ученый Рудольф Клаузиус немногим более 100 лет назад - в 1865 году, когда объяснял невозможность перехода теплоты от более холодного тела к более теплому. В переводе с греческого "энтропия" означает "поворачиваюсь внутрь", то есть "ухожу в себя".

Этот "уход в себя" очень заинтересовал австрийского ученого Людвига Больцмана, и он решил в нем разобраться. В результате глубоких работ ученого появилось в 1872 году такое истолкование энтропии.

Представим себе какую-либо систему, например газ, заключенный в сосуд. Что ее в данном случае характеризует? Определенный объем, давление, температура - то, что принято называть макросостоянием. А чем оно вызвано? Микросостояниями: положением и скоростью частиц в тот или иной момент. В некоторый момент состояние одно, в другой - другое, в третий - третье, и т. д. Иными словами, система из многих состояний выбирает одно. Какое? Это и доказал Больцман: система стремится к неорганизованности, стремится увеличить свою энтропию. Вместе с тем - это общепризнанно - система стремится к равновесию, "ищет" свое самое вероятное состояние. Значит, когда говорят, что энтропия системы возрастает, говорят попросту о том, что система стремится к равновесию? Совершенно верно. Действительно, когда газ находится в равновесии, как бы ни сновали в определенном объеме газа молекулы, как бы ни "дрались" между собой, количество молекул, их скорости движения будут всегда где-то "в середине", всегда близки какой-то средней величине. Тогда энтропия тела, характеризующая его состояние, будет наибольшей. Значит, говорит Больцман, энтропия связана с вероятностью микросостояния тела.

Разобраться в новом для нас понятии поможет нам и "демон" Максвелла- пример, ставший классическим.

"Демон" знаменитого английского ученого максвелла поселился не в одном десятке научных и научно-популярных книг. Суть "демона" в них, естественно, одна и та же, только выражена разными словами. Чтобы не пересказывать этот пример еще раз, возьмем его "в готовом виде" - так, как описал его "отец кибернетики" Норберт Винер:

"Предположим, что в резервуаре находится газ, температура которого везде одна и та же, и что некоторые молекулы этого газа будут двигаться быстрее, чем другие. Предположим далее, что в резервуаре имеется маленькая дверца, через которую газ поступает в ведущую к тепловому двигателю трубу, и что выпускное отверстие этого теплового двигателя при помощи другой трубы соединено через другую дверцу с газовой камерой. У каждой дверцы находится маленькое существо - "демон", - наблюдающее за приближающимися молекулами и открывающее или закрывающее дверцу в зависимости от движения молекул.

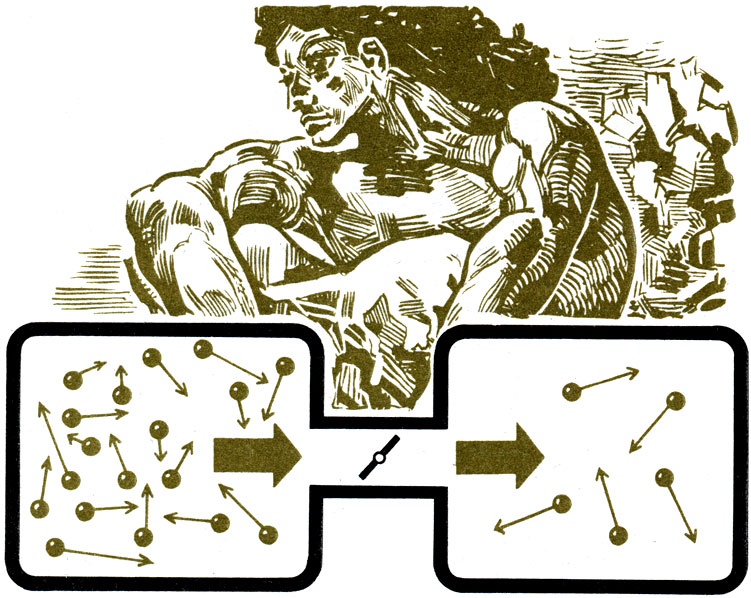
Упрощенная схема 'Демона' Максвелла. Молекулы с длинными стрелками движутся с большей скоростью

В первую дверцу "демон" пропускает выходящие из резервуара молекулы только с высокой скоростью движения и не пропускает молекул с низкой скоростью. У второй дверцы роль этого "демона" совершенно противоположна: он открывает дверцу только для молекул, выходящих из резервуара с малой скоростью, и не пропускает молекул с большой скоростью. В результате этого на одном конце резервуара температура повышается, на другом конце понижается'". Чтобы упростить понимание примера Максвелла с "демоном", Винер предлагает свою аналогию:

"Возможно, мне еще удастся несколько пояснить эту идею на примере толпы, пробивающейся в метрополитен через два турникета, один из которых пропускает людей, если они движутся довольно быстро, а другой - если они движутся медленно. Случайное движение людей в метрополитене предстанет как поток людей, быстро движущихся от первого турникета, в то время как второй турникет пропускает только медленно движущихся людей. Если оба эти турникета соединены проходом с топчаком в нем, то поток быстро движущихся людей будет быстрее поворачивать топчак в каком-то направлении, чем поток медленно движущихся людей будет поворачивать его в обратном, и мы будем иметь источник полезной энергии в случайном движении".

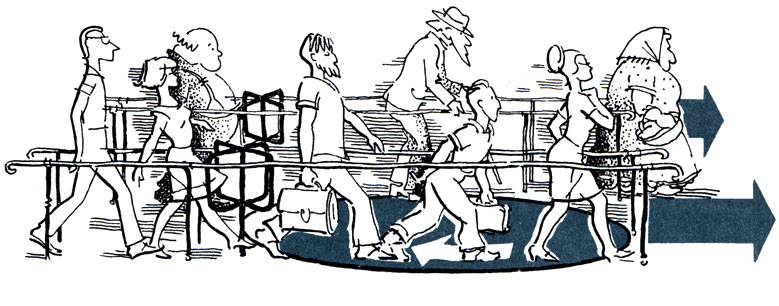
Такой топчак в метро мог бы служить источником полезной энергии при случайном движении толпы

Иными словами, и турникет в метро, и "демон" Максвелла оказываются в состоянии снижать энтропию "во вверенном им хозяйстве". Так как же разрешить тогда это противоречие: "демон" снижает энтропию, а законы физики утверждают возможность только ее возрастания? Парадокс? Да, парадокс. И оставался он им долгое время, пока венгерский физик Л. Сциллард не опубликовал работу под сугубо научным названием: "Об уменьшении энтропии в термодинамической системе при вмешательстве мыслящего существа". Здесь ученый снова обращается к "демону" Максвелла.

Чем же он интересен? Прежде всего тем, что "демон" может действовать только в случае, когда он для своей работы - открывания и закрывания дверей то для быстрых, то для медленных молекул - будет получать дополнительную энергию. Только затрачивая эту энергию, "демон" держит взаперти своих "подопечных": быстрые молекулы в одной стороне, медленные - в другой. Иными словами, только тогда удается "демону" снизить энтропию системы. Но на что же именно тратит этот деятельный "демон" полученную энергию? На "организаторскую деятельность", расплачиваясь энергией за информацию, за знание, куда каким молекулам идти, отвечает Сциллард и доказывает это. Доказательство ученого чрезмерно трудное и специальное. Приводить его здесь не имеет смысла. Поверим так, тем более что выводы Сцил-ларда признаны учеными во всем мире.

Итак, мы получили вывод о связи информации и энтропии. Очень важный вывод, ибо отсюда вытекает положение, что информация находится в обратной зависимости от энтропии. Знаменитый американский ученый Клод Шеннон так и рассматривает информацию: то, что устраняет неопределенность выбора.

Вспомним микросостояния и макросостояния системы Больцмана. Там информация может подсказать нам, как, по какому определенному руслу движутся молекулы, оценить их движение. Таким же образом можно оценить и любую другую категорию, например различное значение букв. На этом основании Шеннон вводит для учета информации формулу энтропии: ведь математике неважно, какие конкретные значения стоят за буквами ее формул.

Этот вывод о глубокой аналогии энтропии и информации настолько интересен, что знаменитый французский физик Луи де Бройль считал это "наиболее важной и наиболее красивой из идей, подсказанных кибернетикой". А крупнейший специалист в области теории информации, выдающийся математик современности А. Н. Колмогоров говорит, что "такие математические аналогии следует всегда подчеркивать, так как сосредоточение на них внимания содействует прогрессу науки".

Вы, конечно, обратили внимание, как осторожны сами ученые в этом вопросе. Дальше аналогий они не идут. Почему? Потому что у энтропии физической и энтропии информационной очень разные "характеры", из-за которых они "ведут" себя по-разному.

Действительно, если при взаимодействии двух тел одно из них увеличивает энтропию, то это всегда бывает за счет другого тела. Но ничего подобного не случается, когда дело идет об информации. Очень остроумно сказал по этому поводу Луи де Бройль: "Если я посылаю вам телеграмму, чтобы известить о падении министерства, я доставляю вам информацию, но в то же время не теряю ее сам".

Тщательному и глубокому анализу подверг содержательность информации и энтропию Норберт Винер. Его интересовал вопрос, почему количество информации и энтропия связаны. И ученый пришел к ошеломляюще простому выводу: потому что они характеризуют реальность, действительность со своеобразных позиций, со своей собственной точки зрения - энтропия и информация рассматривают мир в соотношении хаоса и упорядоченности. Винер так и говорит: энтропия- мера хаоса, количество информации - мера упорядоченности.

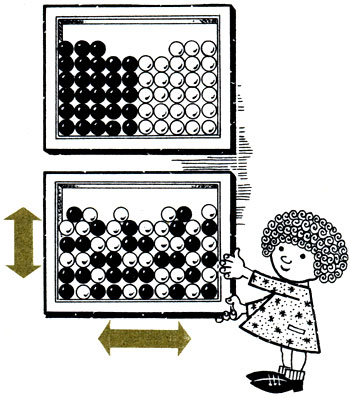
Энтропия простой системы черных и белых шариков, разделенных в ящике, увеличивается от беспорядочных встряхиваний

Башня, которую построил человек - 'целесообразная физическая система',- отличается высокой степенью порядка. Проходят годы, и от случайных, ненаправленных воздействий извне башня развалится и превратится в груду камней-энтропия системы увеличилась

Можно сказать, что наконец некоторая доля ясности внесена в понятие энтропии в физике и теории информации: они отделены одно от другого, мы знаем их "индивидуальные особенности", их "черты характера".

Но дальше идет нечто непонятное на первый взгляд. Стоило ли так упорно проводить "водораздел" между ними, чтобы, как выяснится сейчас, опять идти к единству? В чем заключается этот "обратный ход", в чем его содержание и необходимость?

Давайте для разрешения этих вопросов обратимся к знакомому нам примеру - сосуду с газом. Но теперь анализ будет проводить другой известный ученый - Леон Бриллюэн.

Перед нами снова сосуд с газом. Газ состоит из непрерывно движущихся молекул, и мы просто не знаем, не можем знать ни точного их положения в системе, ни их скорости. Но мы знаем макроскопические характеристики системы: давление, объем, температуру, химический состав. Хотя эти величины мы и можем измерить, но они не дают нам подробного описания "местоположения" молекул. А чтобы вычислить энтропию, мы обязаны учитывать все те внутренние состояния, которые соответствуют именно данному состоянию нашей системы - газа в сосуде. Поэтому естественно, чем меньше мы знаем, как себя ведут молекулы, тем больше неопределенность, тем больше число возможных внутренних состояний. Значит, больше вероятность, больше энтропия.

Правда, не всегда мы такие беспомощные - ничего не знаем о системе. Иногда кое-какие сведения у нас есть. Например, как система образовалась, момент ее возникновения. Это очень нужные данные, они - ключ к получению других, вытекающих отсюда данных, например - распределение плотности и скоростей.

Такие дополнительные сведения для нас очень ценны, потому что они помогают полнее охарактеризовать систему, а значит, снизить энтропию. Тогда выходит, что энтропию мы можем рассматривать как меру недостатка информации, а информацию - как отрицательное слагаемое энтропии, ее "негатив"? Именно так, говорит Бриллюэн, определяя информацию как негэнтропию.

Но так ли это важно, как назвать информацию - собственно информацией или негэнтропией? Оказывается, важно. Негэнтропийный принцип информации объединяет на новой основе энтропию и информацию, говорит, что нельзя их трактовать порознь, они всегда должны исследоваться вместе. И это положение верно для различных, невыразимо далеких одна от другой областей применения - от теоретической физики до примеров из повседневной жизни.

Итак, круг замкнулся. Мы узнали о Клаузиусе, нашедшем для названия нового понятия слово "энтропия". Познакомились с учением Больцмана о связи энтропии и вероятностного микросостояния тела. Узнали о воззрениях Винера на энтропию как меру хаоса. Мы прошли по трудной дороге - от различия к связи. Мы выяснили, какую ответственную роль сыграла энтропия в науке, как помогла она понять многие законы природы. Выяснили и то, как недавно теория информации "повернула" энтропию и заставила науку по-новому взглянуть на нее.

'Демон' открывает двери