
Беседа 5. Управление и математика

Управление и математика
- Не люблю я математику,-заявил вечером Саша.- Скука. Ну кому интересно решать задачу про бассейн с двумя трубами. По одной вода вливается, по другой - выливается. Ясно, если вторую трубу не закрыть, это будет долго тянуться. Или: "Из двух сел одновременно навстречу друг другу вышли два пешехода. Встретились они через четыре часа. Расстояние между селами тридцать шесть километров, скорость первого пешехода четыре километра в час. С какой скоростью шел второй пешеход?" Ну скажи, папа, кто сейчас пойдет на тридцать шесть километров пешком?
- Туристы пойдут,- ответил Николай Николаевич, беря в руки задачник.
Полистав задачник,он прочитал вслух: - "Месячная зарплата рабочего сто пятьдесят рублей. На покупку ботинок и рубашки он израсходовал шестнадцать процентов зарплаты. Сколько стоит рубашка, если ботинки стоят семнадцать рублей?" - И добавил: - Чем плохая задача?
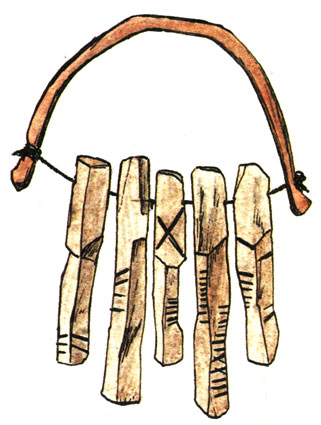
Числа изображались камешками, костяшками, зарубками, узлами и веревках

Когда у человека появилась потребность считать? Что он считал: прожитые дни, детей, шкуры животных, кремнёвые ножи? Об этом можно только гадать. Во всяком случае, простейшие счетные приборы археологи находят в культурных слоях, насчитывающих тысячи лет. Числа изображались камешками, костяшками, зарубками, узлами на веревках. Такие простейшие средства счета предметов были неудобны для изображения больших чисел. Скажем, для изображения числа «20» требовалась пригоршня ракушек, а для «2000»? Мешок! Вот почему человек приспособил для счета пальцы рук, а потом сделал счеты.
Счеты применяются в бухгалтерском деле и в наши дни. Но все реже и реже. В конце прошлого века они были потеснены механическими арифмометрами. Лет двадцать назад появились так называемые ЭКВМ - электронные клавишные вычислительные машины. Это были увесистые изделия нашей промышленности, пригодные только в качестве настольного прибора. Масса первых 'Искр' достигала 12 килограммов!

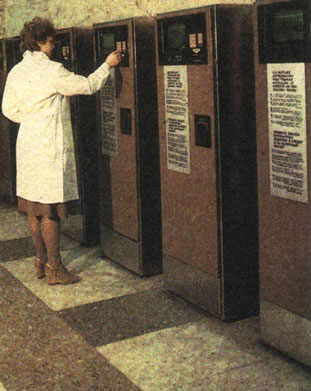
С развитием микроэлектроники компьютеры здорово 'похудели'. И не только сбавили в весе и в аппетите на электроэнергию. Они вышли из таинственных лабораторий, куда допускались лишь высокие интеллектуалы в белых халатах. Крупные машины 'отпочковали' целую армию малых, шагнувших в дома, магазины, библиотеки. Терминал - это компактное конечное устройство ЭВМ. На снимке: терминалы в кулинарном магазине радиозавода ВЭФ
- В магазине цены на все крупно написаны, ничего считать не надо,- уныло сказал Саша.- Нет, не очень-то интересно.
Николай Николаевич задумался на несколько минут, а потом сказал так:
- Нет, я не согласен с тобой. Математика - интересная наука, без нее в жизни не обойтись. Вот мы говорили об оптимальном управлении. Тебе же было интересно. Там, где добиваются оптимального управления, получают большой выигрыш времени, сил, денег. Мы рассмотрели много задач управления и пришли к выводу, что без расчетов, без математики оптимизации не осуществить. Вот ты гадал, как ехать лучше - через центр или по кольцу. Без вычислений тут ничего доказать нельзя.
- Подумаешь - математика! - буркнул Саша.- Расчеты-то простые: подсчитали время на два варианта, сравнили между собой два числа да и выбрали лучший вариант.
- Подсчет числовых значений критериев оптимальности для разных вариантов - простейший способ оптимизации. Хорошо, когда нужно сравнить между собой всего несколько вариантов. А если этих вариантов тысячи, десятки тысяч? А если больше? Вон при игре в шахматы может быть такое количество вариантов, что все компьютеры мира сто лет должны работать, чтобы найти выигрывающие ходы. Мы с тобой изучали разные машины как объекты управления. Вспомни тот же самолет - разве в воздухе не бесчисленное количество дорог?
- Однако вычислительные машины в шахматы играют, и еще как! - возразил Саша.- Я сам играл с компьютером на выставке.
- Верно, играют. И только потому, что существуют математические методы, позволяющие резко сократить число просматриваемых вариантов. Для оптимизации управления любой машиной, любой работой, вообще для решения любой задачи на оптимизацию требуется составить математическую модель, то есть представить все, чем надо управлять, в виде математических формул. Модель - это подобие чего-либо. Есть физические модели зданий, мостов, кораблей, самолетов. Делают, к примеру, маленький самолет и начинают продувать в специальной аэродинамической трубе. Это физическая модель самолета.
На физической модели можно измерить, скажем, силу сопротивления воздуха. Только модель не летит, а стоит в трубе на месте, и мощный вентилятор гонит на нее воздух. На такой модели ищут оптимальную форму самолета, при которой сопротивление воздуха получается наименьшим. А можно поступить по-другому: написать формулу, в левой части которой будет сила сопротивления воздуха, а справа от знака равенства - геометрические размеры самолета, числа, определяющие гладкость его обшивки, вязкость воздуха и так далее. Изменяя, варьируя числа в правой части формулы, можно определить оптимальное решение математически, не затрагивая много средств на обычные опыты, на физические эксперименты. Если же надо управлять автомобилем, ракетой или самолетом на ходу, в движении, то математическая модель вводится в память машины, в запоминающее устройство бортового управляющего компьютера - того самого умного автомата, о котором мы говорили с тобой в прошлый раз. В такой автомат должна быть введена полностью программа всех вычислений. Программа вычислений составляется в строгом соответствии с управляющим алгоритмом. Да! Придется пояснить, что такое алгоритм. Это набор правил выполнения какой-либо работы, например правил решения задачи. Правила требуется записать строго и четко, чтобы результат решения задачи был один и тот же, вне зависимости от того, кто выполняет вычисления - человек или машина. Теперь вернемся к начальной точке: что, собственно, требуется делать, чтобы зарядить управляющий компьютер оптимизирующей программой?

Существуют разные модели. Есть модели математические, есть и физические. 'Дерево решений' - графическое отображение процесса принятия решения

Уменьшенная копия грузовика удобна для продувки в аэродинамической трубе

Шахматы позволяют моделировать состязание умов и способностей рассчитывать последствия принятых решений
Поведение физических систем можно моделировать с помощью компьютера
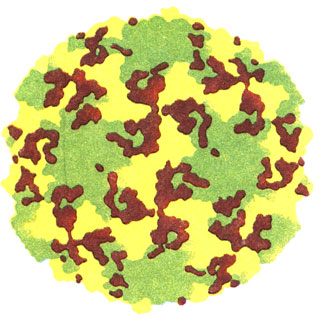
Компьютерная модель вируса полиомиелита. Как видно, модель - не обязательно уменьшенное подобие какого-либо объекта. Модель может быть больше объекта в тысячи раз

Так выглядит машинный зал вычислительного центра средней мощности. На переднем плане - накопители информации на магнитных вращающихся дисках. Пакет сменных дисков устанавливается на дисковод, и магнитные головки начинают считывать и записывать информацию
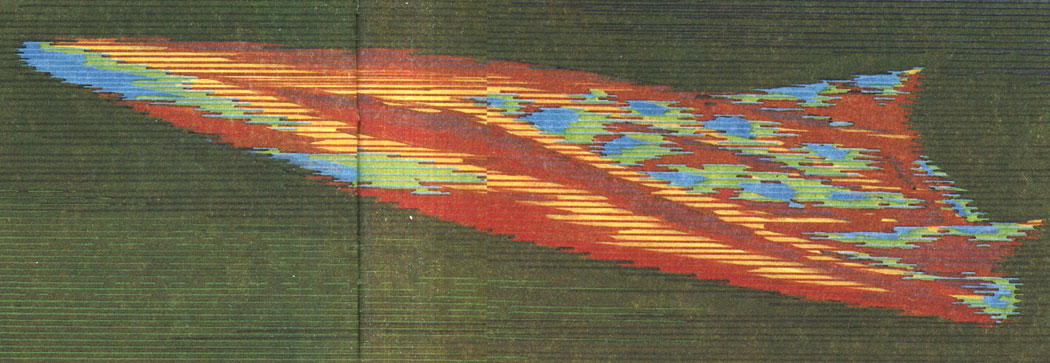
Картина аэродинамических испытаний модели самолета. Исследования на моделях, особенно на математических, позволяют экономить средства и время
- С выбора критерия нужно начинать,- бодро сказал Саша,- это-то я уже усвоил.
- Правильно. Затем необходимо составить математическую модель работы той машины, которой будем управлять. Ну и конечно, выберем математический способ оптимизации. Потом разработаем управляющий алгоритм и программу. А программу запишем в память электронной вычислительной машины. Как видишь, тайн в этом деле еще немало, но не так уж все страшно. Главное - знать разделы математики, в которых изучаются способы или методы оптимизации. Все вместе такие разделы обычно называют исследованием операций. Исследование операций - это разработка обоснованных решений. Решения - основа управления, их приходится принимать на каждом шагу. Как из множества всевозможных решений, допускаемых обстоятельствами, наилучшим образом выбрать одно определенное решение? Можно ли не перебирать все существующие решения, а сразу отбросить те из них, которые заведомо будут не самыми лучшими? Кажется, все это - сухие материи. Далековато от жизни... Давай-ка возьмем бумагу и карандаш да попробуем решить одну задачу. Тут не потребуется знать сложные теоремы, писать громоздкие формулы. Нужно уметь складывать числа, и больше ничего. Ну, немножко сообразительности потребуется, зато можно овладеть основами одного из самых мощных современных математических методов, который называется динамическим программированием.

В лаборатории фотоупругости. Мосты, здания, плотины и другие сооружения моделируются с помощью эпоксидных пластмасс. Затем модель просвечивают яркой лампой. На экране можно увидеть точную картину поведения модели под нагрузкой. Цветные полосы покажут все слабые места, все зоны концентрации нагрузок в деталях и узлах сооружений. И только после исследования даются обоснованные советы проектировщикам и строителям.
Модель Вселенной на ранней стадии своего развития, короче, юная Вселенная

У вертолета нет точно заданной трассы, как у трамвая или поезда. У него бесчисленное количество траекторий полета. Можно круто карабкаться на высоту, можно подбираться к той же заданной высоте 'блинчиком', по отлогой траектории. А нужно найти единственный вариант - оптимальный
Николай Николаевич взял чистый лист бумаги, карандаш и прозрачную линейку.
- Какой же взять пример? - задумчиво сказал он.- Хотя я не авиационный инженер и не летчик, небо с детства привлекало меня. Давай-ка попробуем решить вот такую задачу. Пусть в нашем распоряжении будет большой вертолет. Нужно взлететь с земли, набрать высоту тысяча метров и разогнать машину до скорости двести сорок километров в час. Конечно же, требуется добиться этого с минимальными затратами горючего.
- Критерий,- важно вставил Саша,- по которому необходимо найти оптимальное решение,- расход топлива.
- Правильно. Понемногу ты, я смотрю, усвоил научные термины в области управления. Итак, критерий есть. Теперь нужна математическая модель. Модель всегда содержит упрощения, иначе можно потерять много времени и запутаться. Давай разобьем полет винтокрылой машины на шаги. Будем считать, что на каждом шаге можно делать что-то одно: либо набирать скорость, либо высоту. Пусть величина шага по высоте будет двести метров, по скорости - тридцать километров в час. Все это нарисуем в виде решетки.
На листе бумаги получилось вот что:
высота - 400 м
высота - 200 м
на земле
0 км/ч 30 км/ч 60 км/ч
Николай Николаевич пояснил:
- Числа означают расход горючего на каждом шаге. Например, если набирать скорость прямо над землей до скорости тридцать километров в час, потребуется пятнадцать литров. Если взлететь по вертикали на двести метров, потребуется четырнадцать литров. Когда машина будет на высоте двухсот метров, потребуется еще тринадцать литров, чтобы подняться до четырехсот метров. Остальное понятно.
Когда он кончил чертить, получилась действительно решетка с числами, обозначающими расход топлива для полета из точки А (земля) в точку В (высота 1000 м, скорость 240 км/ч). Под решеткой Николай Николаевич подписал: "Рис. 1".
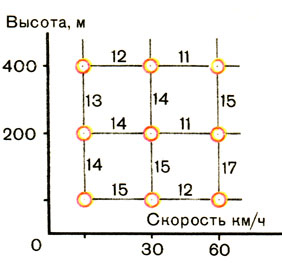
Начало построения решетки: два шага по высоте и по скорости
- А где же математическая модель? - спросил Саша.
- Сейчас. Модель будет очень простая, куда проще, чем задачи из вашего учебника. Посмотри на рисунок. Сколько шагов от точки А нужно сделать нашему вертолету, чтобы выйти в точку В?
Саша подсчитал и сказал:
- Тринадцать. Почему-то считается, что тринадцать - не очень счастливое число.
- Чтобы тебя успокоить, возьмем четырнадцатый шаг - нулевой. Вообрази, что в точку А мы прилетели без всякого расхода горючего. Что нужно сделать, чтобы подсчитать общий расход топлива на пути из точки А в точку В ?
- Сложить расход по шагам,- не задумываясь, сказал Саша.- Это и есть модель? Математическая?
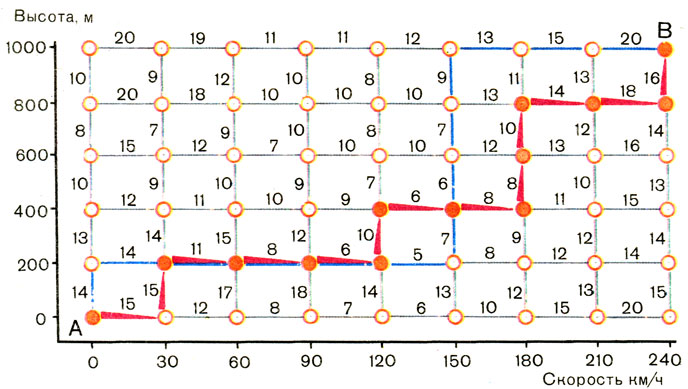
Рис. 1. Весь процесс взлета представлен в виде решетки
На каждом 'шаге' находится оптимальное решение. Правило: всякая часть оптимального плана есть оптимальный план!
- Да. Формула для вычисления суммы. Общий расход топлива равен расходу топлива на первом шаге плюс расход на всех последующих шагах,- подтвердил Николай Николаевич.- Однако это еще не все. Критерий мы выбрали, процесс полета упростили - представили его в виде формальной схемы, вот этой самой решетки. Исходные данные - расход топлива на каждом шаге - я взял просто так, для примера. Потом эти числа можно будет уточнить. Теперь оптимизация. Попробуй-ка определить, сколько возможных путей, траекторий полета, существует? Перебери их и найди оптимальный.
Саша взял коричневый карандаш и начал водить им по решетке. Через пять минут он сказал:
- Сдаюсь. Много путей - все не перебрать, и я вот выделил из них всего три. Мне лично кажется, что оптимальная траектория такая...
Он нарисовал красные стрелки от узла А решетки до узла В, потом выписал числа на пути полета вертолета. Получилось вот что:
15 + 15 + 11 + 8 + 6 + 10 + 6 + 8 + 8 + 10 + 14 + 18 + 16 = 145 литров.
Посмотрев на Сашины стрелки, Николай Николаевич сказал:
- Проверка нужна. Существуют математические методы, позволяющие отбросить заведомо худшие решения. Динамическое программирование основано на том, что оптимальное решение принимается на каждом шаге. Всякая часть общего оптимального плана должна содержать оптимальный план, оптимальное решение. Попробуем применить эту идею к нашей задаче. Начнем, пожалуй, не с начала, а с конца, с точки В.
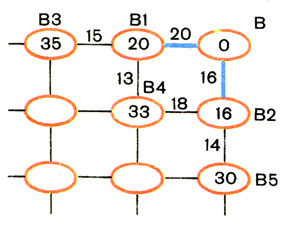
И Николай Николаевич нарисовал кусочек решетки, ее правый верхний угол (рис. 2). Синим карандашом провел линии от точек В1 и В2 к точке В. В кружке В он написал "0", в кружке В1 - "20", а в кружке В2 - "16".
- Видишь, в точку В можно попасть из двух точек: из точки В1 и точки В2. Поэтому я в кружки записал тот расход топлива, который для этого нужен. Ясно, что в кружке В появился НОЛЬ - цель достигнута, расхода топлива нет. Теперь внимание! Самое главное: путь в точку В из точки В4. Тут два варианта - через В1 и через В2.
Саша в уме быстро сложил числа и сказал:
- Лучше через В1 - расход тридцать три литра, а через В2 - на литр больше.
- Вот в этом все дело. Я рисую синюю линию от В4 к В1, а в кружок В4 ставлю "33". Как видишь, мы нашли часть оптимального плана. Осталось заполнить остальные кружки и пометить синими линиями части оптимальной траектории нашего вертолета. Давай этим и займемся.
Хотя нужно было складывать только целые числа, Саша для верности включил микрокалькулятор. Когда все кружки были заполнены, решетка приобрела такой вид, как на рис. 3.
- Теперь от точки А вернемся к точке В по синим линиям, прорисовывая в конце линий стрелки. Подсчитываем, что получилось,- сказал Николай Николаевич.
Получилось вот что: 14 + 14 + 11 + 8 + 6 + 5 + 7 + + 6 + 7 + 9 + 13 + 15 + 20 - 135 литров.
- Это и есть оптимальная траектория. Самая-самая. Лучше не найти,- заключил Николай Николаевич.- Если теперь ввести в бортовой компьютер вертолета эту траекторию и заставить его следить за строгим соблюдением оптимального режима набора заданной высоты и скорости, то можно получить солидную экономию горючего. Без математики у нас с тобой получалось сто сорок пять литров, а с математикой - сто тридцать пять. Выигрыш существенный. Математика и управление стоят очень близко друг к другу.
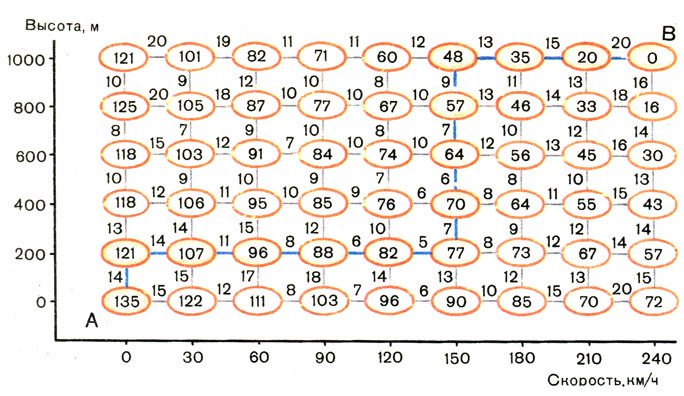
Рис. 3. Оптимальное для заданных условий решение: набор заданной высоты и скорости полета при минимальном расходе топлива
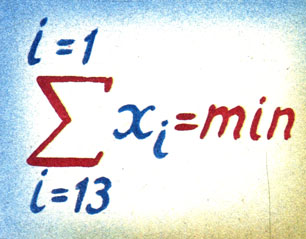
Так выглядит формула для подсчета расхода топлива
|
ПОИСК:
|
© ROBOTICSLIB.RU, 2001-2019
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'