6. Математическое описание двигателя постоянного тока

Работа двигателя постоянного тока в статическом режиме (вращение с постоянной угловой скоростью) может быть охарактеризовано рядом уравнений, связывающих его основные параметры:

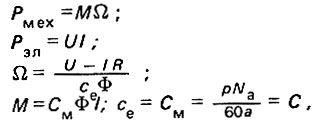
где 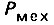- механическая мощность на валу электродвигателя; 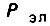- электрическая мощность двигателя; M - вращающий момент на валу двигателя; Ω - угловая скорость двигателя; U - напряжение двигателя; I - ток двигателя (среднее значение); Φ - магнитный поток возбуждения двигателя; C - конструктивная постоянная двигателя; p - число пар полюсов двигателя; 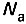- число параллельных ветвей обмотки.

Динамические режимы удобнее всего анализировать с помощью математической модели, соответствующей уравнениям, характеризующим двигатель при различных внешних воздействиях.

Эквивалентная схема двигателя постоянного тока приведена на рис. 18.

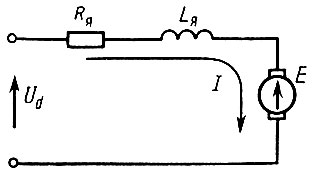
Рис. 18. Эквивалентная схема двигателя постоянного тока

По первому закону Кирхгофа приложенное напряжение уравновешивается противо-эдс двигателя E, падением напряжения на активном сопротивлении 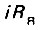и эдс электромагнитной индукции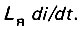

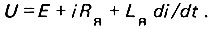
Противо-эдс двигателя может быть выражена через угловую скорость Ω, магнитный поток Φ и конструктивный коэффициент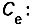

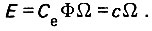
Вращающий момент двигателя связан с током соотношением

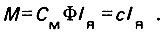
Изменение скорости в динамических режимах происходит под действием динамического момента, равного разности момента двигателя и момента статической нагрузки:

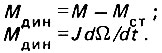
Разгон двигателя происходит под действием динамического момента, преодолевающего инерционные массы нагрузки и двигателя с моментом инерции J. Разгон начинается, как только вращающий момент двигателя превысит момент статической нагрузки. Таким образом, время разгона зависит от величины динамического момента и скорости его нарастания.

Время нарастания вращающего момента двигателя зависит от времени нарастания тока 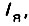которое определяется электромагнитной постоянной времени:

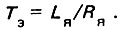
Электромеханическая постоянная времени 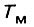характеризует зависимость времени разгона от момента инерции и возможного динамического момента двигателя:

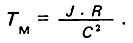
Подставив в уравнение баланса напряжений выражения его составляющих через 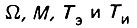и производных 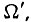получим дифференциальное уравнение двигателя постоянного тока с постоянным возбуждением:

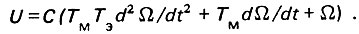
Однако решение дифференциальных уравнений вызывает некоторые затруднения, поэтому дифференциальные уравнения можно решить алгебраическим путем, заменив символы дифференцирования d/dt оператором p.

Уравнение двигателя в операторной форме:

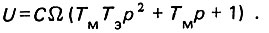
Этому уравнению соответствует структурная схема, показанная на рис. 19.

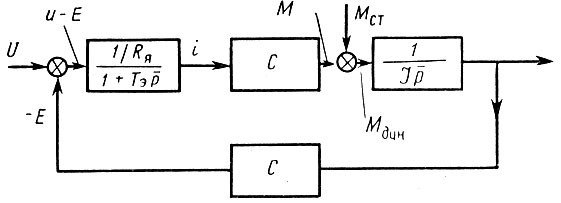
Рис. 19. Структурная схема двигателя постоянного тока

Передаточная функция двигателя 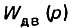представляет собой отношение выходного параметра к входному: выходной параметр двигателя - скорость, входной - напряжение на якоре:

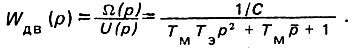
Приведенная передаточная функция двигателя необходима для расчета переходных процессов, возникающих в регулируемом электроприводе, представляющем собой сложную систему автоматического управления. Кроме того, она может применяться для определения реакции двигателя при скачкообразном изменении напряжения на его якоре.

Пример. Пусть требуется определить кривую изменения скорости двигателя во времени при скачкообразном изменении напряжения якорной цепи. Известно, что

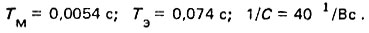
Тогда

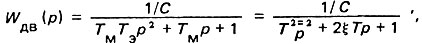
где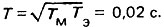

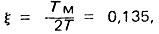
так как двигатель в данном случае представляет собой колебательное звено (Т²_м<4Т_мТ₃). Переходная характеристика двигателя

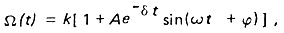
где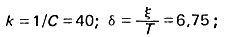

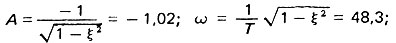
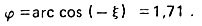
Таким образом,

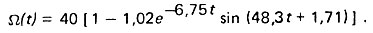
Как следует из рис. 20, период колебаний равен 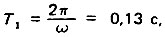а логарифмический декремент затухания

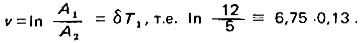
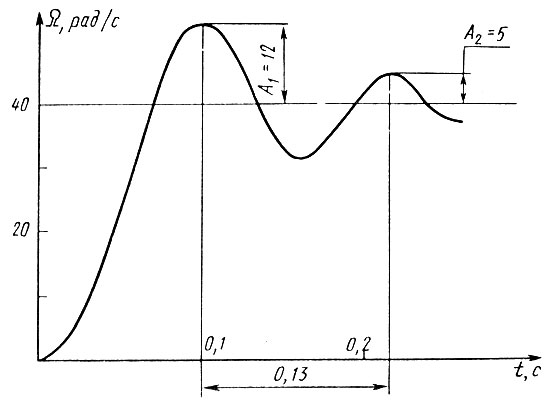
Рис. 20. Переходный процесс при пуске двигателя