Группа кодовая

Группа кодовая

Группа кодовая - набор символов для 
отображения частей сообщения, 
передаваемого по каналам связи. 

"В каждой строчке только точки..."

Есть такая игра "Горячо - холодно". В ней весь разговор, все "команды" передаются только двумя символами. Удаляешься от предмета поиска - "холодно", приближаешься - "горячо". В результате подачи условных знаков играющий иногда решает довольно сложные задачи поиска.

А нельзя ли двумя символами кодировать и текст?

Вот ряд условных знаков: только точки и тире. Что они означают?

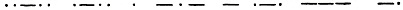
Если вы знаете азбуку Морзе, то прочтете слово "электрон". Значит, различные комбинации двух знаков позволили закодировать весь алфавит.

Когда вы внимательно рассматривали азбуку Морзе, то, вероятно, заметили, что некоторые буквы передаются одним-двумя знаками: Е - точка, Т - тире, А - точка, тире, И - две точки, и т. д. Другие же - четырьмя или даже пятью: Ж - три точки, тире, X - четыре точки, Ч - три тире, точка, Э - две точки, тире, две точки.

Попробуем определить, из скольких знаков должна состоять кодовая группа, чтобы можно было записать все буквы одинаковым количеством нулей и единиц.

Вначале возьмем только два знака - 0 и 1. Получим:

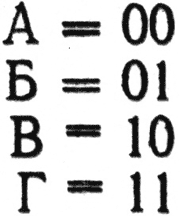
На этом наши возможности оказались исчерпанными. Ничего не поделаешь: 2²=4.

Попробуем теперь взять три знака:

И снова предел: 2³=8.

Если мы опять прибавим один знак, то получим 2⁴=16. 16 комбинаций хватит только на половину нашего алфавита.

При пяти знаках: 25 = 32 - мы достигаем наконец нужного нам числа комбинаций.

Вот один из примеров такого кода:

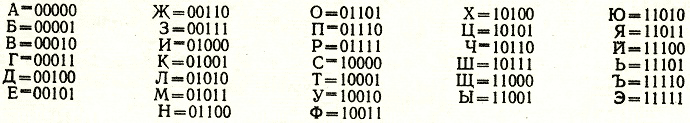
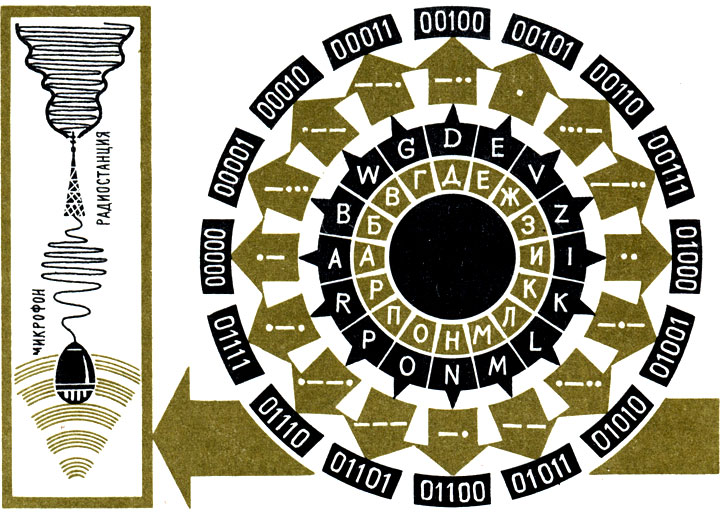
Посмотрите, как можно одну и ту же букву закодировать разными символами

Теперь подсчитаем, из скольких знаков должна состоять кодовая группа, чтобы все цифры от 0 до 9 записывать тоже одинаковым количеством нулей и единиц. И здесь, оказывается, двух и трех знаков мало. А вот четырех достаточно, они дают 16 комбинаций, а нам нужно всего 10.

Вот как будут выглядеть цифры в закодированном виде:

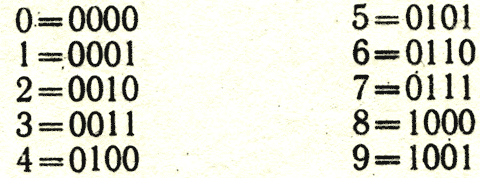
Не думайте, что эти коды цифр и букв единственные. Их может быть очень много - миллиарды.

Воспользуемся нашим кодом и закодируем слово "кибернетика" и число "13".

Вот слово "кибернетика", скрытое под комбинациями нулей и единиц: 01001 01000 0001 00101 01111 01100 00101 10001 01000 01001 00000.

Число "13" запишется как 0001 0011.

Для того чтобы сообщение попало в машину, чтобы она могла производить с ним нужные операции, есть специальные - очень важные - устройства. Это своего рода ворота, через которые только и можно попасть в машину. Но ворота не простые, а волшебные: они превращают число в код, делают его удобным для машины.

Совершенный "антипод" кодирующего устройства - устройство декодирующее, или, как его иначе называют, дешифратор. Дешифратор - "волшебник наоборот"; его задача из кода сделать "просто число".

Кодирование и декодирование считаются одними из самых важных логических операций "электронного мозга". И по праву. Ведь это они позволяют машине "уметь" преобразовывать числа в код, работать с ними внутри машины, снова преобразовывать их в нужный код при выдаче уже обработанной инфор!мации. Можно сказать, что без этих устройств машина как без рук.

Интересно, что с кодированием в жизни мы встречаемся на каждом шагу. Не только когда заменяем обычный текст символами или переводим знаки одного алфавита в другой, но и когда идет передача от источника к адресату: при передаче по радио в микрофон попадают звуковые колебания, они преобразуются в колебания электрического тока, затем в электромагнитные. В этих случаях кодирование одной физической величины идет заменой на другую.

В таком "алфавите" может быть различной и физическая природа "букв". "Буквами" могут быть и пометки чернилами на бумаге, и дырки в бумажной ленте, и пробитые отверстия в картонных картах. "Буквами" могут быть и различные положения вращающихся элементов, и электрические импульсы, и световые сигналы.

На принципе перекодировки основана работа телетайпов - аппаратов, которые без всякого участия человека превращают обычный текст в присвоенные каждой букве комбинации электрических сигналов, а комбинации электрических сигналов - обратно в буквы.

Набирая тот или иной номер телефона вращением диска на аппарате, вы, вероятно, не подозреваете, что занимаетесь перекодировкой десятичного кода в серию электрических импульсов, которые для наглядности опять-таки можно записать с помощью 0 (нет импульса) и 1 (есть импульс).

Смотрите, как это выглядит:

'В каждой строчке только точки...'