Двоичная система счисления

Двоичная система счисления

Позиционная система счисления,
основанием которой служит число 2. 

Все из 0 и 1

Когда человек научился считать, то он стал считать на пальцах, загибая их по одному. Этот счет (его со временем стали называть десятичной системой счисления) оказался настолько удобным, что живет до сих пор.

Всем нам эта система знакома с первого класса. Мы знаем ряд чисел от 0 до 9. Знаем, что разряды отличаются один от другого десятичным основанием. Эта система кажется нам и самой простой, и самой удобной.

Так считал и знаменитый французский ученый Блез Паскаль, создавший первую вычислительную машину. Свое механическое счетное колесо он сделал десятичным: в нем было десять зубьев. С тех пор в десятичной системе счет можно было осуществить не только вручную с помощью 10 пальцев, но и механически - с помощью 10 зубьев колеса.

Затем та же десятичная система "перекочевала" и в электромеханические счетные машины. В них был применен шаговый искатель с 10 позициями.

И первые электронные вычислительные машины пользовались все теми же десятью "пальцами" - десятью триггерами. На десятичной системе счисления работала, например, американская машина "ЭНИАК". Но для нее требовалось столько дорогого оборудования, что конструкторы стали искать способы сократить число триггеров.

В основу своих поисков инженеры и математики положили двоичную- двухпозиционную - природу элементов, "органов" вычислительной техники.

Возьмите, к примеру, электронную лампу. Она может находиться только в двух состояниях: или проводит электрический ток - "открыта", или не проводит его - "заперта". А триггер? Он тоже имеет два устойчивых состояния. Двоичны и запоминающие элементы.

Почему же не использовать тогда двоичную систему счисления? Ведь в ней только две цифры: 0 и 1. А это очень удобно для работы на электронной машине.

И новые машины стали считать с помощью 0 и 1.

Не думайте, что двоичная система - современница электронных машин. Нет, она намного старше. Двоичным счислением люди интересуются давно. Особенно сильным это увлечение было с конца XVI до начала XIX века.

Знаменитый Г. В. Лейбниц считал двоичную систему простой, удобной и красивой. Он говорил, что "вычисление с помощью двоек, вознаграждение его длиннот, является для науки основным и порождает новые открытия... При сведений чисел к простейшим началам, каковы 0 и 1, везде появляется чудесный порядок".

По просьбе ученого в честь "диадической системы" - так тогда называли двоичную систему - была выбита медаль. На ней изображалась таблица с числами и простейшие действия с ними. По краю медали вилась лента с надписью: "Чтобы вывести из ничтожества все, достаточно единицы".

А потом как-то сразу о двоичной системе замолчали, забыли. В течение почти 200 лет на эту тему не было издано ни одного труда. Вернулись к ней только в 1931 году, когда были продемонстрированы некоторые возможности практического применения двоичного счисления.

Эта система, как и десятичная, подчинена строгим законам. Но в десятичной за основание берется 10, а в двоичной - 2. В десятичной системе в каждом разряде - одна из десяти различных цифр, в двоичной- только две. В десятичной системе каждый разряд в 10 раз больше предыдущего, в двоичной - в 2 раза.

Посмотрите, как курьезно выглядят привычные нам числа, записанные в двоичной системе:

"Еще в младших классах он проявлял себя весьма смышленым мальчиком. С задачами, которые сверстники решали полчаса, он справлялся за какие-то 101 - 11О (5-6) минут. Одаренный недюжинным умом и неиссякаемой энергией, этот счастливец закончил вуз на год раньше срока, за 11 лет (3 года), и в возрасте 1010 000 лет (20) возглавил научно-исследовательскую лабораторию".

А теперь попробуем разобраться в двоичной записи.

На стр. 83 таблица отчетливо показывает, что чем меньше знаков-цифр в одном разряде для записи в двоичной системе, тем больше надо разрядов, чтобы представить данное число. Возьмем, например, из таблицы число 8. В двоичной системе для его представления понадобятся четыре разряда: 1000.

Теперь возьмем другую запись в двоичной системе - 1111. Самая правая, последняя цифра так и будет единицей. Но уже следующая - высшего разряда - больше ее только в два раза и означает 2, третья опять в два раза больше - 4, четвертая, соответственно, - 8.

Попробуем записать какое-нибудь число, допустим 1017, в двоичной системе. Для этого, как и в десятичной системе, разлагаем его на разряды, но разряды здесь выглядят по-иному. Начнем с низшего, с 7. В числе 7 одна четверка, одна двойка, одна единица: 7 = 4 + 2 + 1. Эту запись можно сделать по-другому: 1*2²+1*2¹ + 1*2⁰. Следовательно, в каждом из этих разрядов ставим по 1-111.

Затем, идет число 10. Оно состоит из одной восьмерки и одной двойки: 10=8+2 = 1*2³+1*2²+1*2¹+1*2⁰. Заметили, здесь нет единиц и четверок, поэтому вместо них мы ставим нули и записываем число так: 1010.

Так же можно разложить и все следующие разряды. А все число 1017 запишется как 512+2564+128+64+32+16+8+1 = 1*2⁹ + 1*2⁸+1*2⁷+1*2⁶+1*2⁵+1*2⁴+1*2³+1*2²+1*2¹+1*2⁰. Записываем по разрядам и получаем 1111111001.

Конечно, вы хотите знать, как производят действия с такими "громоздкими" числами.

Оказывается, по правилам, похожим на применяемые в десятичной системе. Правда, со своими особенностями.

Вот как читается правило счета в двоичном счислении:

"Поскольку имеются лишь две цифры, правило переноса формулируется так: когда в какой-либо разряд, в котором стоит 1 (самая старшая цифра), добавляется еще одна 1, этот разряд возвышается в 0 и посылает единицу переноса в следующий, старший разряд. При непрерывном добавлении единиц в данный разряд его показания все время меняются на обратные: если в этом разряде стоял 0, он заменяется на 1, а если стояла 1, она заменяется на 0 и при этом выдается единица переноса".

Давайте, руководствуясь этими правилами, сложим самые простые числа: 1 + 1.

Записываем:

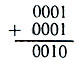
Сложим теперь 8+3.

Запись будет выглядеть так:

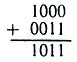
Для основных арифметических действий в двоичной системе составлены таблицы:

Математики утверждают, что арифметические действия в двоичной системе проще, чем в десятичной. В двоичной системе проще даже извлечение корней. Вероятно, и вам трудно будет с ними не согласиться, если вы немного потренируетесь в двоичной арифметике. Только надо знать, что вычитание здесь заменяется сложением. Делается это так: вместо вычитания данного числа к уменьшаемому прибавляют число, являющееся дополнением к вычитаемому, то есть дополняющим его до следующей высшей разрядной единицы.

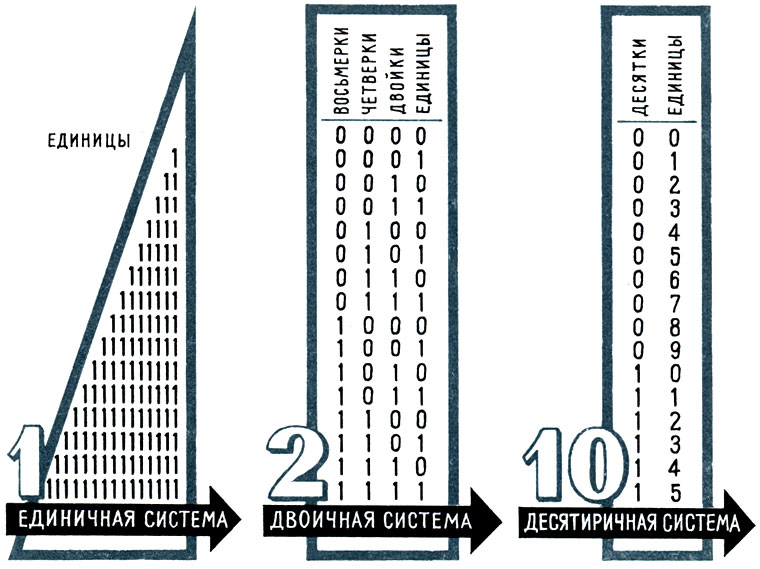
Сравнение записи чисел в единичной, двоичной и десятиричной системах

Допустим, из числа 10011 нужно вычесть 101. Сначала уравняем количество разрядов у чисел, приписав к вычитаемому спереди два нуля - 00101. Дополнением к вычитаемому (до 100000) будет 11011.

Прибавим это число к уменьшаемому:

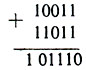
Единицу слева отбросим - получим 01110. Действительно, 19-5=14,

Умножение же сводится к переписыванию множимого с соответствующими сдвигами и сложению. Например:

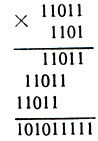
Деление тоже сводится к последовательному вычитанию, а оно, в свою очередь, заменяется сложением.

Как видите, все многообразие математических операций сводится к одному простому арифметическому действию - сложению.

Итак, все преимущества двоичной системы, столь непривычные нам из-за традиции оперировать всегда и везде системой десятиричной, мы знаем. Осталось назвать ее недостаток: двоичной системой пользуются только вычислительные машины, только они в ней безпраничные хозяева. Правда, им не страшны длинные, однообразно-унылые ряды нулей и единиц, которые подчинены монотонным правилам двоичной арифметики. Машина пересчитывает вереницы нулей и единиц с очень большой скоростью. Так что с этим недостатком двоичной системы, оказывается, совсем не трудно мириться.

Даоичная система счисления