Теория игр

Теория игр

Математическая дисциплина, 
устанавливающая количественные з
акономерности в конфликтных ситуациях. 

"Красные" против "синих"

Ни один человек за всю свою жизнь не переиграл всех игр, которые есть на свете, - игр существует множество. У каждой свои правила, свои особенности. Хоккей, например, отличается от футбола, прятки - от "казаков-разбойников", домино - от "крестиков-ноликов", "морской бой" - от игры в слова, и т. д. и т. п. И все-таки эти совершенно непохожие игры принципиально - в главном - совершенно одинаковы.

В чем эта одинаковость? В столкновении интересов.

Вася и Петя играют в "морской бой". Каждому во что бы то ни стало хочется выиграть: столкновение интересов.

"Раз, два, три, четыре, пять! Я иду искать!" - предостерегает ребят тот, кто водит. Он должен найти кого-либо, а задача прячущихся - не попасться ему на глаза. Опять столкновение интересов.

На футбольном поле встречаются прославленные наши команды "Динамо" и "Спартак". Кто-то из них должен стать победителем. "Динамо" безусловно приложит к этому все силы. И "Спартак" полон решимости победить. Столкновение интересов.

Столкновение интересов есть не только в играх. Оно случается часто, намного чаще, чем мы предполагаем. Проследите под этим углом зрения один из своих обычных дней. Сколько раз сталкивались ваши интересы с чьими-то!

В повседневной жизни, в практической деятельности очень часто встречаются ситуации, когда разные люди имеют разные интересы и располагают разными путями в достижении разных целей. Иными словами, всем нам часто приходится сталкиваться с конфликтными ситуациями. Настолько часто, что конфликты, столкновения интересов" признаны даже одной из главных тем в художественной литературе.

Мы преодолеваем конфликт, когда играем с приятелем в шахматы.

"Проходит через конфликт" и ребенок, который ни за что на свете не хочет спать вопреки желанию родителей.

Конфликтна ситуация между продавцом на рынке - он, конечно, хочет подороже продать товар - и покупателем, который хочет купить подешевле.

Примером политического конфликта в капиталистических странах служат разногласия между враждующими политическими партиями во время предвыборной кампании.

Конфликт между зайцем и лисой как биологическими видами в условиях борьбы за существование.

Конфликт... В нашем представлении это дело запутанное, подчас субъективное, часто эмоциональное и всегда - трудное. Всегда нелегко разрешить конфликтную ситуацию. А вот современная математическая наука считает возможным не только провести анализ конфликтной ситуации, но и "просчитать", как должен вести себя каждый партнер, чтобы достигнуть цели. У математики есть свой подход к столкновению интересов. Им занимаются специалисты по теории игр.

Для того чтобы провести математический анализ конфликта, надо прежде всего самым строгим образом "обнажить", "проявить" столкновение интересов, сделать их столь же четкими и не вызывающими никаких сомнений, как в игре, где и непосвященному ясно, кто борется против кого.

Математики так и поступают: они строят упрощенную модель конфликтной ситуации, которую называют игрой. Ее-то, эту модель-игру, и ведут по определенным правилам. А для простоты - и, пожалуй, по привычке и понятности - в математическую теорию игр "перекочевала" и обычная игровая терминология. Участников игры называют игроками, результат - выигрышем или платежом.

Правда, смысл терминов здесь несколько иной. В теории игр "игроком" могут быть и несколько человек с определенным интересом, которые борются против одного или, наоборот, против большого количества противников, которые тоже признаны "игроком". Значит, игрок - это просто одна группа интересов. Футбольный матч, с точки зрения теории игр, будет "просчитываться" как один игрок против одного. В этом смысле он не отличается от шахматной партии.

Выдающийся французский математик Луи Борель еще в начале нашего века предпринял издание большого, многотомного "Курса теории вероятностей и ее приложений". Предпоследний том был посвящен "Приложениям к азартным играм". Ученый подвел в нем итог своим длительным исследованиям азартных игр, которыми он интересовался как математик. В теорию игр Борель внес смелые и оригинальные идеи.

До него все ограничивались рассмотрением игр, где ход игры определялся случаем, а не игроками. Борель попытался найти математическую формулировку игр, когда течение игры зависело от умения игроков. Со временем многие ученые развили теорию игр до такой степени,

что она стала гораздо шире теории азартных игр и ее результаты нашли большое применение.

Обычно так всегда и бывает - игру намного труднее рассказать, проще показать, как в нее играют. И нам легче будет разобраться в основных понятиях теории игр, если мы обратимся к одному из многочисленных примеров, которые приводят специалисты.

Представим себе двух игроков А и Б. Каждый из них независимо один от другого пишет на бумажках одно из чисел: 0, 1, 2. Затем они показывают бумажки друг другу и складывают написанные числа. Если сумма четная, Б уплачивает А число рублей, равное сумме чисел. Если сумма нечетная, А платит ее Б.

Запись чисел и предъявление их друг другу называются ходом игры. Сознательный выбор системы последовательных ходов именуется стратегией. Игрок принимает решение: "В таких-то обстоятельствах я буду поступать так-то". А выигрыш одного или другого противника, как вы уже. знаете, носит название платежа.

Постараемся проследить течение игры.

Результаты всех возможных ходов можно заранее перечислить. А пишет 0 (нуль), Б тоже пишет 0. Сумма равна нулю, и никто из игроков ничего не получает.

А пишет 0, Б пишет 1 - сумма число нечетное. А проигрывает, а Б выигрывает один рубль.

А снова пишет 0, Б пишет 2 - сумма четная. Б теперь проигрывает, выигрывает два рубля А.

Такой же перебор можно произвести и с числами: (1, 1), (1, 2), (2, 1) и (2, 2). Нетрудно заметить, что число возможных комбинаций, из которых независимо друг от друга будут выбирать А. и Б, всего 3x3=9.

Обозначим стратегию А писать 0 через А₁, 1 - через А₂, а 2 - через А₃. Так же обозначим стратегии и для Б - Б₁ Б₂, Б₃. Тогда все возможные выигрыши и проигрыши (как "выигрыш" со знаком минус) можно представить таблицей.

Таблица, в которой записаны выигрыши и проигрыши противников в результате применения всех возможных стратегий, называется платежной матрицей, а игра - матричной игрой.

Что видно из анализа платежной матрицы? Прежде всего противник А должен признать противника Б достаточно умным, ибо он обязательно применит такую стратегию, чтобы сделать выигрыш А наименьшим при всех его стратегиях. Во-вторых, игрок А должен из всех минимально возможных выигрышей выбрать ту стратегию, которая обеспечит ему максимальный выигрыш. Такой стратегией для А является А\ - всегда писать нуль. Применяя ее, он проигрывает не более 1 рубля.

Рассуждая аналогично, за игрока Б, мы установим, что он тоже будет выбирать стратегию, по какой он меньше всего проиграет. Для этого надо посмотреть платежную матрицу по столбцам и найти наименьшую сумму, которую может выиграть А. Суммы выигрышей А и Б выписаны под таблицей.

Цель теории игр - выработать рекомендации для каждого из противников, как вести себя в "сражении". Пользуясь этими математическими советами, противники могут выбрать наивыгоднейшую, оптимальную стратегию, чтобы обеспечить и той и другой стороне наилучший исход игры. Правда, практически никогда одна какая-либо стратегия не применяется, партнеры довольно часто меняют ее, придерживаются смешанных стратегий.

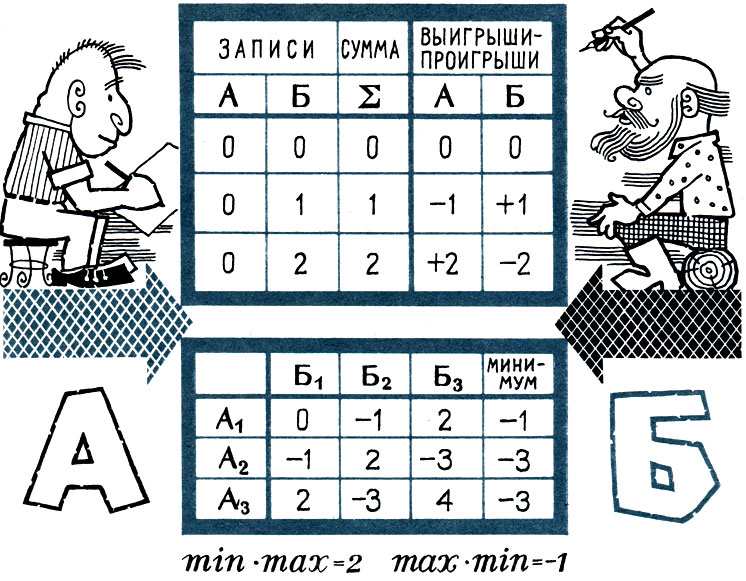
Стратегии игроков А и Б и платежная матрица

Однако какая бы игра ни шла, как бы ни меняли А и Б стратегии, всегда противники хотят действовать противоположно, интересы их сталкиваются. А стремится, чтобы наименьший выигрыш, который он думает получить, был как можно большим (это называют максимином). Б, в свою очередь, стремится сделать как можно меньшей ту наибольшую сумму, которую он должен отдать А (это называется минимаксом).

Как видите, главная цель игрока состоит в том, чтобы получить наибольший выигрыш у своего искусного противника, поставившего перед собой противоположную задачу: обыграть своего противника.

Значит, игрок желает выиграть, но не может рассчитывать на промах противника. Игрок в теории игр знает: как бы ни была хороша его стратегия, противник обязательно сделает наилучший контрход. Поэтому при подсчете платежей игрок учиты-тывает наихудшие, которые может получить.

Но как количественно определить, кто же из противников (таких точных, таких бесстрастных, не делающих ошибок, логически рассуждающих) выиграет? Определить сравнительно легко. В каждой игре существует некоторый платеж, который получает хороший игрок, сражаясь против хорошего же игрока. Такой платеж называется ценой игры. Она-то и определяет выигрыш: мы никогда не сможем выиграть больше цены игры, если наш противник не делает ошибок.

Разберем с этой целью еще одну простую игру с двумя противниками и двумя стратегиями. Ее условно называют "Бомбардировочной операцией".

Предположим, что два бомбардировщика "синих" вылетели на задание. Один из них несет бомбы, а другой - оборудование для создания помех радиолокаторам, различную аппаратуру для определения ущерба и т. п.

Бомбардировщики летят в таком строю, что первый находится под большей защитой пушек второго бомбардировщика, чем второй - под защитой первого. Есть опасения, как бы носитель бомб не был сбит в результате атак истребителей "красных". Проблема заключается в следующем: какой из бомбардировщиков должен нести бомбы - первый или второй? И какой из них должен быть атакован "красными"? То есть как должен вести себя каждый из противников, чтобы добиться наивыгоднейшего результата?

Здесь возможны следующие стратегии:

"Синие"-1 - носитель бомб в менее выгодном положении.

"Синие"-2 - носитель бомб в более выгодном положении.

"Красные"-1 - атаковать бомбардировщик в менее выгодном положении.

"Красные"-2 - атаковать бомбардировщик в более выгодном положении.

Предположим, что шансы носителя бомб выжить равны 60 из 100, если он будет атакован в менее выгодном положении; и 80 из 100, если его атакуют в более выгодном положении; и 100, если он не будет атакован вообще.

Запишем это так, как принято в теории игр, - матрицей.

"Красные" и "синие", естественно, должны менять свои стратегии. Подсчитано, что на 20 случаев применения первой стратегии будет 40 случаев применения второй. Выходит, "синие" должны предпочесть защищенное положение бомбардировщика в отношении 40:20. А "красные" должны в том же соотношении (40:20) атаковать защищенный бомбардировщик.

Теперь мы можем подсчитать цену игры для "синих":

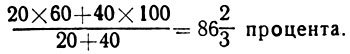
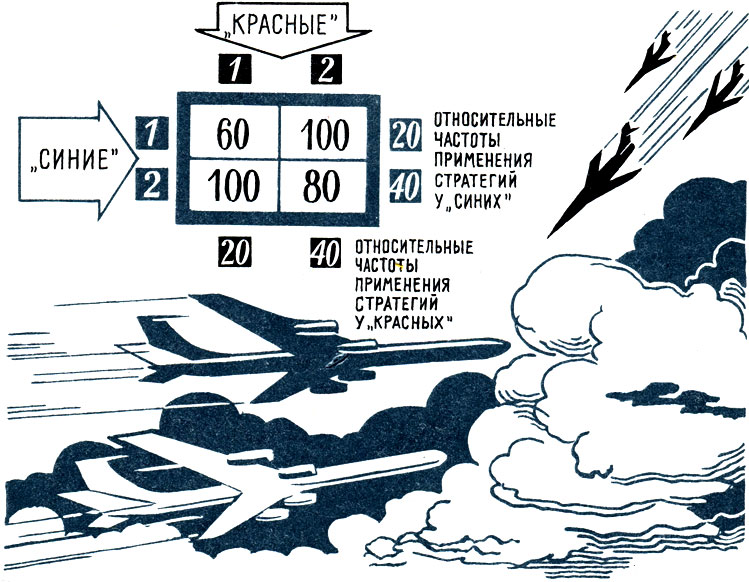
Игра под условным названием 'Бомбардировочная операция'

А теперь после довольно утомительных логических рассуждений познакомимся со скандальной историей, случившейся несколько лет назад в игорных домах Европы.

...Сначала на них никто не обращал внимания. Эти молодые люди заходили в казино поглядеть на игру в рулетку. Они останавливались возле игорных столов и записывали в блокноты номера выигрышей. "Просто так, любопытства ради",- отвечали они тому, кто их спрашивал: "Зачем?"

А спустя два месяца в Монте-Карло, в этой столице игорных домов, разразилась гроза. Снова пришли те молодые люди. Но теперь они не записывали выигрыши, а сами стали играть. И беспроигрышно. Поразительно! Необъяснимо!

Журналисты захотели найти объяснение. И считают, что нашли. Оказывается, молодые люди не ради любопытства записывали номера выигрышей - непонятные вереницы чисел. Мало того, они еще их и закодировали. И после этого переслали в Лондон своему компаньону. Тот обработал их с помощью электронно-вычислительной машины. По-видимому, машина сделала то, что не под силу человеку: обработав миллионы чисел, она разгадала несколько точных вариантов выигрышей.

Правда, многие специалисты утверждают, что такое могло произойти только в том случае, если у рулетки был какой-то постоянный дефект. Возможно, он и был, но о нем не знали ни владельцы игорного дома, ни участвовавшие в подсчетах люди.

Но сколько же машине понадобилось вести расчетов? Неизвестно. Однако известно другое. Один американский математик установил: чтобы определить точные выигрыши в очко, надо проанализировать 34 миллиона вариантов расклада карт. Правда, такая задача для человека непосильна, но на помощь жаждущему выигрышей математику пришла электронная машина. Он задал ей 10 тысяч человеко-лет работы, и машина рассчитала варианты беспроигрышных партий.

В "американском случае" машинное руководство к действию (алгоритм поиска вариантов) было составлено так, чтобы изыскивать повышение вероятностей благоприятного исхода. Именно с этой целью "перебирала" машина горы цифр и чисел, строя свою "игру" против вымышленного противника по законам теории игр.

Право же, не стоило создавать целое направление в математике, законно заметите вы, чтобы помогать выигрывать в азартные игры! Конечно, теория игр создана не для этого (да, кстати, заметим, что в играх, подобных рулетке и лото, не существует такого руководства к действию, которое давало бы всегда строго определенную выигрышную стратегию).

Азартные игры, модели игр служат тем пробным камнем, на котором теория игр пытается проверить куда более серьезные задачи.

С помощью теории игр кибернетики стремятся выработать целесообразную "линию поведения" для многих и многих систем, ведущих борьбу против другой системы.

Что же скрывается за понятием борьбы одной системы против другой? Таких примеров чрезвычайно много, с ними сталкиваются разные специалисты. Например, теорию игр можно применить к задачам военной связи, к военно-воздушной обороне (конечно, задачи там намного сложнее решенной нами бомбардировочной операции), к задачам,которые приходится решать командиру в сражении.

Под углом зрения теории игр можно рассматривать и работу экспериментатора, который составляет программу действий - план экспериментов.

Их можно рассматривать как игру, где противниками выступают ученый и нервная система животного, которую он изучает.

Против ответных действий "противника"-потребителя "играет" экономист, планирующий работу производящего предприятия.

В некоторых случаях и взаимоотношения так называемых юридических лиц (предположим, в суде) можно рассматривать как игру, в которой противники стремятся к противоположным целям.

И в большинстве случаев в "играх" приходится иметь дело с цифрами, цифрами, цифрами: проделывать головокружительное количество вычислений.

Не случайно, значит, учат машины играть в разные игры: в домино, в шашки, в пятнадцать и, конечно, в шахматы. Шахматы, дающие астрономическое число вариантов партий - 2*10¹¹⁶! - открывают большой простор для исследований.

Целый год длился "машинный матч" между программами советской и американской машин. Умению провести матч ученые придавали очень большое значение: от "шахматного дарования" машин, то есть от программ, которые составляют математики, зависело решение сложных проблем в теории игр. А это, в свою очередь, позволяет решать и важные научные, народнохозяйственные и военные задачи.

Вот, оказывается, для чего математики на бумаге разыгрывают сражения "красных" и "синих", вот для чего учат электронно-вычислительные машины вести разные игры с полным знанием дела, быть опытным, маститым противником.

'Красные' против 'синих'