Многозвенные манипуляторы

Определение

Термин многозвенный манипулятор (многосуставный манипулятор) практически имеет тот же самый смысл, что и термин манипулятор с несколькими степенями подвижности. Поскольку словосочетание "степень подвижности" будет очень часто встречаться в дальнейшем изложении, уточним, что оно означает.

Говорят, что тело имеет n степеней подвижности, если оно способно совершать ровно n различных независимых видов перемещений. В робототехнике это понятие используется в качестве количественной характеристики сложности конструкции роботов (главным образом манипуляторов и захватных устройств). Для иллюстрации введенного термина на рис. 3.25, а показаны примеры механических конструкций, обладающих одной степенью подвижности. В частности, это поворот одного звена относительно другого, вращение цилиндрического стержня вокруг собственной оси симметрии, а также возвратно-поступательные движения цилиндрического стержня вдоль этой оси. Две степени подвижности имеют конструкции, приведенные на рис. 3.25, б: среди них трехзвенник i, образованный последовательным соединением двух конструкций, показанных на рис. 3.25, а, а также универсальный шарнир ii, позволяющий одной и той же точке перемещаться в двух взаимно перпендикулярных направлениях.

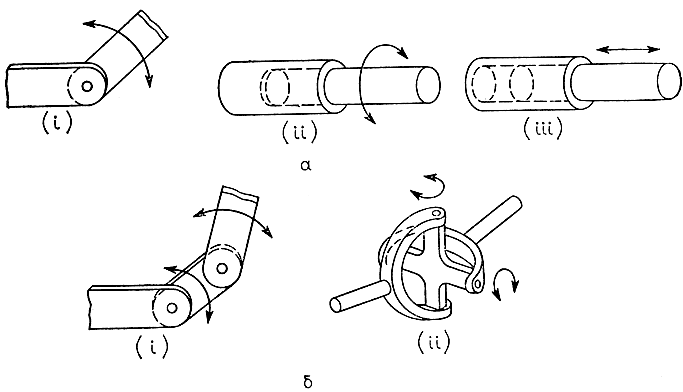
Рис. 3.25. Кинематические механизмы. а - кинематические механизмы с одной степенью подвижности: (i) качание, (ii) поворот вокруг собственной оси, (iii) возвратно-поступательное перемещение; б - кинематические механизмы с двумя степенями подвижности: (i) последовательное соединение двух шарниров качания, (ii) универсальный шарнир

Как правило, обычные промышленные роботы обладают пятью-шестью степенями подвижности. Однако часто встречаются роботы, имеющие менее четырех степеней подвижности. Их популярность обусловлена простотой использования и надежностью эксплуатации в условиях реального производства. В настоящее время в научно-исследовательских лабораториях широко проводятся эксперименты по использованию так называемых интеллектуальных роботов. Среди разработанных моделей этих роботов известны не только обычные конструкции с пятью-шестью степенями подвижности, но и манипуляторы с числом степеней подвижности, превышающим семь.

♦♦♦ Заметим, что в робототехнике в общее число степеней подвижности, обычно не включают степени подвижности захватного устройства. Напротив, в области протезирования по традиции учитываются все имеющиеся степени подвижности. Поэтому, если речь заходит о протезе руки, обладающем шестью степенями подвижности, следует иметь в виду, что собственно рука имеет только пять степеней и еще одна степень приходится на сжатие-раскрытие кисти. Как будет показано ниже, можно упрощенно полагать, что многозвенная конструкция, имитирующая руку человека, насчитывает семь степеней подвижности.

Многозвенные манипуляторы, которые могут быть использованы в качестве механических устройств, заменяющих руки человека при выполнении самых разнообразных операций, выделяются из общего класса манипуляционных устройств благодаря следующим особенностям: сложной многозвенной конструкции руки и шарнирным механизмам, обеспечивающим те же степени подвижности звеньев, что и локтевой сустав человека (эта особенность характерна лишь для более узкого класса рассматриваемых манипуляторов - многозвенных антропоморфных манипуляторов).

Управление такими столь сложными механизмами, как многозвенные манипуляторы, также может оказаться довольно сложным. Даже при выполнении простейшей операции - перемещение захватного устройства многозвенного манипулятора из точки А в точку В - для расчета управляющей информации требуется выполнить большой объем вычислений. Рассмотрим основные вычислительные методы, применяемые для управления многозвенными манипуляторами, а также основные особенности практического использования этих методов.

Управление многозвенными манипуляторами

Проанализируем более детально задачу о перемещении захватного устройства из точки А в целевое положение, т. е. в точку В. Если манипулятор имеет всего одну степень подвижности, то управление перемещением в заданную точку не вызывает никаких затруднений - достаточно всего лишь рассчитать величину угла поворота θ (рис. 3.26, б). Совсем иная ситуация возникает в том случае, когда манипулятор помимо вращательного может совершать и возвратно-поступательное движение. Тогда роботу придется основательно "поломать голову" над тем, какими же из следующих способов движения воспользоваться:

1) сначала совершить поворот руки на угол θ, а затем выполнить поступательное перемещение на величину r в радиальном направлении до достижения заданной точки В;

2) сначала выполнить поступательное движение на величину r, а уже затем поворот на угол θ;

3) выполнить одновременно поворот до предельного угла 0 и перенос до предельного расстояния r (в данном способе вид траектории, соединяющей точки А и В, не оговаривается). Данный метод управления называется позиционным управлением, или РТР (point-to-point);

4) разбить диапазон вращения θ и линейного перемещения r на мелкие сегменты, провести аналогичное разбиение величины выходного управляющего сигнала и, подавая на приводы полученные после разбиения управляющие сигналы через интервалы . времени, соответствующие прохождению одного сегмента в разбиении диапазонов θ и r, переместить захват из точки А в точку В по траектории, близкой по форме к прямолинейной. Такой метод управления движением называется контурным управлением или сокращено СР (continious path), а методы разбиения диапазонов вращательного θ и линейного r перемещений на маленькие сегменты, включая выбор расположения точек, ограничивающих эти сегменты, - интерполяцией.

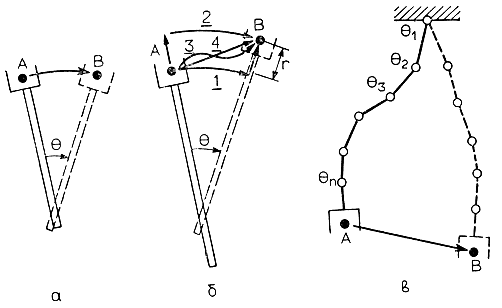
Рис. 3.26. Простое перемещение, выполняемое манипуляторами с одной, двумя и многими степенями подвижности. а - манипулятор с одной степенью подвижности; б - манипулятор с двумя степенями подвижности; в - многозвенный манипулятор

Траектории движения захвата манипулятора, характерные для каждого метода управления, показаны на рис. 3.27. Описанный анализ не вызывает затруднений, если речь идет об управлении реальными манипуляторами, число степеней подвижности у которых не больше трех. В противном случае, чтобы заставить захват переместиться из исходной точки А в целевую точку В, необходимо рассчитать соответствующие траектории движения для каждого из звеньев (рис. 3.20, в). Удовлетворительное решение подобных задач уже не может быть найдено с помощью описанного выше простого интуитивного подхода. В самом деле, для вывода законов согласованного изменения координат θ₁, θ₂, ..., θ_n по каждой из степеней подвижности, приводящего к переходу манипулятора из текущего состояния в заданное, может потребоваться выполнение чрезвычайно сложных расчетов. Изложение математических основ управления многозвенными манипуляторами начнем с решения довольно простой задачи вида: какое положение занимает в данное время захват, если текущие значения углов θ₁, θ₂, ..., θ_n для всех степеней подвижности манипулятора известны?

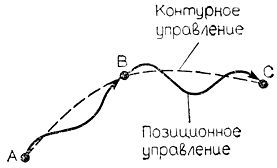
Рис. 3.27. Различия между контурным и позиционным принципами управления

Вычисление положения многозвенного манипулятора

Для того чтобы по известным величинам вращения или линейного перемещения по каждой из степеней подвижности найти положение захватного устройства, а также всего манипулятора или какой-либо из его частей, обычно применяют один из двух методов расчета - матричный или векторный. В основе того и другого лежит принцип преобразования координат с помощью матриц преобразования.

Особенности векторного метода

Параллельный перенос и вращение системы координат

Обозначим оси исходной прямоугольной системы координат через х, у, z; оси системы координат, полученной после применения к исходной операции параллельного переноса, - через х', у', z', а оси системы, полученной после применения к последней операции вращения, - через х₁, у₁, z₁ (рис. 3.28). Кроме того, обозначим базисные векторы старой и новой систем координат соответственно как (i, j, k) и (i₁, j₁, k₁). Тогда эти системы координат можно записать в следующем виде:

старая система координат {O; i, j, k};

новая система координат {O₁; i₁, j₁, k₁}.

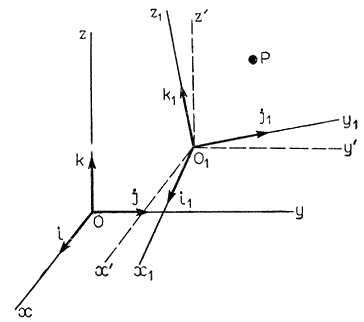
Рис. 3.28. Параллельный перенос и вращение системы координат

Возьмем произвольную точку Р с координатами Р (x, y, z) в старой системе координат и Р (х₁, у₁, z₁) в новой системе. Между этими координатами существует соотношение вида

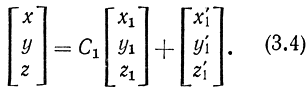
Переменные x'₁ y'₁, z'₁ характеризуют величину параллельного переноса вдоль каждой из соответствующих осей при преобразовании систем координат O → O₁. Другими словами, эти переменные являются координатами точки О₁ (начало новой системы координат О₁), выраженными в старой системе координат.

Множитель С₁ в уравнении (3.4) называется матрицей преобразования координат, которая в данном случае описывает операцию вращения и состоит из следующих элементов:

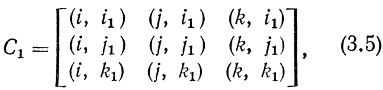
где пары типа (i, i₁) - скалярное произведение базисных векторов.

Рассмотрим еще одну систему координат: {O₂; i₂, j₂, k₂}. Предположим, что переход к этой системе координат от системы {О₁; i₁, j₁, k₁} осуществляется с помощью матрицы преобразования С₂. Оказывается, что в этом случае для перехода от системы координат {О; i, j, k} к системе {О; i₂, j₂, k₂} достаточно воспользоваться матрицей преобразования С₁·С₂, полученной в результате перемножения двух известных матриц преобразования.

В общем случае матрица преобразования координат, описывающая n-шаговое вращение исходной системы координат, может быть представлена произведением матриц преобразования, описывающих вращение на каждом отдельном шаге, т. е.

К рассмотренному способу перехода от одной системы координат к другой с помощью матриц преобразования, описывающих вращение, приходится довольно часто прибегать при вычислении положения многозвенного манипулятора. Это обусловлено широким распространением вращательных соединений в конструкциях манипуляторов промышленных роботов. В связи с этим целесообразно выписать в явном виде матрицы преобразования, описывающие вращение вокруг каждой из осей прямоугольной системы координат.

Пусть система координат с осями х, у, z повернулась вокруг оси х на положительный (при отсчете по правилу правого винта) угол θ_i (рис. 3.29). Матрицу преобразования, описывающую данный тип вращения, обозначим через С_х. Вычисляя ее элементы непосредственно из уравнения (3.5), получаем

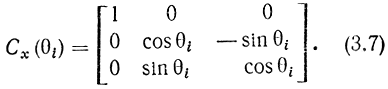
Аналогично находятся матрицы преобразования координат С_у и C_z, описывающие вращение вокруг осей у и z. Заменив для удобства обозначения cosθ_i и sinθ_i на c_i и s_i соответственно, запишем полученные матрицы в явном виде

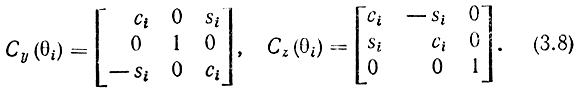
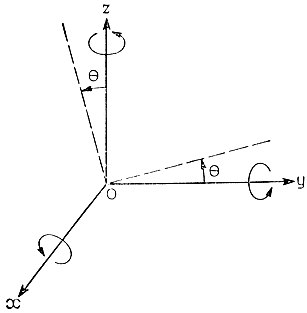
Рис. 3.29. Поворот системы координат вокруг оси х

Обобщение метода преобразования координат

Правая часть уравнения (3.4) представляет собой сумму двух членов. Если вместо обычных матриц воспользоваться матрицами размерности 4×4, то уравнение (3.4) может быть приведено к виду

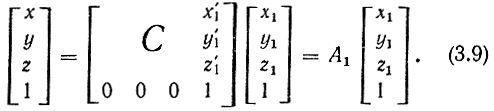
Из выражения (3.9) следует, что А₁ есть не что иное, как 4×4-матрица преобразования координат, описывающая переход от системы {О; i, j, k} к системе {O; i₁, j₁, k₁}.

Если теперь с помощью матрицы преобразования А₂ перейти от системы координат {O₁} к системе {O₂}, то общая матрица преобразования, описывающая переход {О} → {O₂} аналогично матрице С в случае 3×3-матриц, может быть представлена произведением двух матриц перехода: А₁·А₂. В общем случае 4×4-матрица преобразования, описывающая я-шаговый переход от первоначальной системы координат к n-й, задается произведением вида

Матрицам С_х, С_у, С_z (см. (3.7), (3.8)) соответствуют 4×4-матрицы преобразования координат

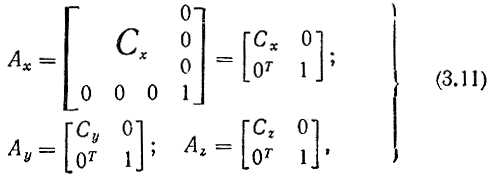
где 0 - трехмерный нулевой вектор-столбец, а 0^Т - полученный транспонированием нулевой вектор-строка.

С помощью 4-мерных вектор-столбцов, 4-мерных вектор-строк и 4×4-матриц можно описывать не только вращение систем координат, но и параллельный перенос. В частности, матрица преобразования координат L_x, описывающая параллельный перенос системы координат вдоль оси х на величину l^х в положительном направлении (рис. 3.30), имеет вид

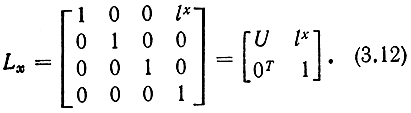
Здесь U - единичная матрица, а вектор l_x = [l^x 0 0]^T. Аналогично матрицы преобразования L_y, L_z, описывающие переход от одной системы координат к другой в результате параллельного переноса вдоль осей у и z, записываются как

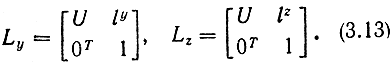
В этих выражениях l_y = [0, l^y, 0]^Т и l_z = [0, 0, l^z]^T.

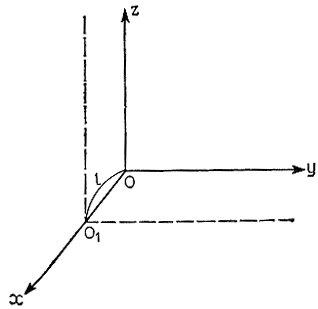
Рис. 3.30. Параллельный перенос системы координат вдоль оси х

Таким образом, если воспользоваться формой записи в 4×4-матрицах, то характерные различия в структуре матриц L и А исчезают. Следовательно, серия переходов от одной системы координат к другой, в которой операции вращения и параллельного переноса некоторым образом чередуются, может быть описана одной 4×4-матрицей B_total. В частности, эта матрица может выглядеть как

Поскольку имеют место соотношения

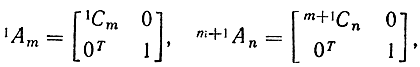
произведение (3.14) удобно преобразовать к виду

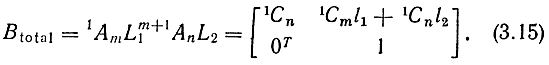
Из уравнений (3.4), (3.9) и (3.15) находим, что координаты (х₁, y₁, z₁) начала системы координат, к которой был осуществлен переход, в первоначальной системе координат выражаются как

Полученное выражение проясняет физический смысл элементов первых трех строк четвертого столбца в развернутом представлении матрицы (3.15). Таким же образом можно установить, что 3×3-матрица C_total, описывающая результирующее преобразование координат, полученное путем последовательного применения всех заданных операций вращения, имеет вид

♦♦♦ Заметим, что в промышленной робототехнике помимо рассмотренных вращательных и поступательных механизмов широко используются манипуляторы с так называемым скользящим, или телескопическим, механизмом соединения звеньев. Очевидно, что приведенный математический аппарат полностью пригоден для описания и этого типа соединений. Следует, однако, иметь в виду, что элемент l^х вектора l_x [(3.12)-(3.15)] в данном случае становится переменной величиной.

Пример применения 4×4-матриц для расчета положения манипулятора

В качестве иллюстрации метода расчета положения манипулятора с помощью выведенного выше общего уравнения (3.15) определим позицию и ориентацию запястья механической руки антропоморфного манипуляционного устройства, разработанного в Японском научно-исследовательском центре проблем механики. Кинематическая схема этого манипулятора (сокращенно MELARM-I) показана на рис. 3.31. Поскольку манипулятор MELARM-I предназначен для воспроизведения двигательных возможностей руки человека, его кинематика также приближена к кинематике руки, и, следовательно, механические соединения всех звеньев обеспечивают только вращательное перемещение.

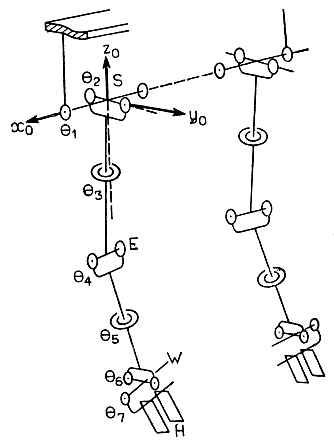
Рис. 3.31. Антропоморфный манипулятор MELARM-I

Как следует из рис. 3.31, пространственная позиция локтевого шарнира Е в жестко связанной с плечевым шарниром системе координат ^СХ₀ (x₀, y₀, z₀) может изменяться только за счет вращения на углы θ₁, θ₂, совершаемого при помощи двух вращательных механизмов плечевого шарнира. Таким образом, позиция точки Е может быть определена сравнительно легко. Однако, если требуется определить не только позицию, но и ориентацию оси вращения локтевого шарнира (т. е. ориентацию локтевого звена), приходится помимо углов θ₁ и θ₂ принимать во внимание возможность поворота на угол θ₃. В результате задача становится не такой тривиальной, как в случае определения только позиции. Продолжая анализ кинематической схемы манипулятора, замечаем, что для определения трехмерной позиции запястья W в системе координат локтевого шарнира S помимо преобразований, связанных с вращениями на углы θ₁, θ₃, следует последовательно добавить еще одно вращение координат, обусловленное поворотом локтевого звена в локтевом шарнире на угол θ₄. Кроме того, при определении позиции W, очевидно, потребуется учитывать длину плечевого звена l₁ и длину локтевого звена l₂. Наконец, выражение для позиции кисти с захватным устройством (в дальнейшем - просто "кисти") Н в системе координат локтевого сустава S будет зависеть от всех углов θ₁ ..., θ₇, и длин l₁, ..., l₃. Следовательно, решить задачу определения позиции запястья W или кисти S без применения специальных математических методов почти невозможно. В то же время, если воспользоваться изложенным выше общим методом перехода от одной системы координат к другой, то пространственное положение любой части сложного многозвенного манипулятора может быть найдено в результате механического выполнения тривиальных математических действий. В частности, таким образом можно непосредственно определить положение запястья W в трехмерной системе прямоугольных декартовых координат ^СХ₀, жестко связанной с плечевым шарниром. Для этого потребуется осуществить цепочку переходов с помощью преобразований вращения на углы θ, ..., θ₅ и параллельного переноса на расстояния l₁ и l₂ от одной системы координат к другой в следующей последовательности ^СХ₀ → ^CX_S → ^СХ_Е → ^CX_W (рис. 3.32). В результате этих преобразований сразу получается 4×4-матрица, описывающая позицию и ориентацию новой (связанной с запястьем) трехмерной прямоугольной декартовой системы координат ^CX_W; причем если интерес представляет только позиция связанной с запястьем точки W, то преобразование вращения на угол θ₅ можно не выполнять.

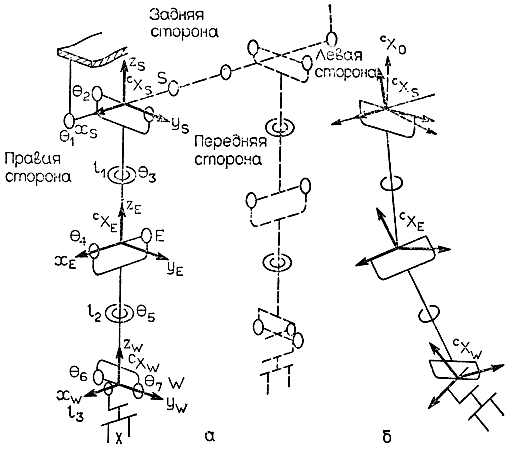
Рис. 3.32. Преобразование координат в результате последовательных поворотов по каждой из степеней подвижности

В рассмотренном примере позиция запястья определяется главным образом значениями углов наклона плеча θ₁ и θ₂, а также длинами плечевого и локтевого звеньев l₁ и l₂ соответственно. Для конструкции, показанной на рис. 3.31, линейные размеры всех звеньев являются константами. Однако на практике применяется большое количество промышленных роботов с телескопическими, или скользящими, соединениями, допускающими удлинение-сокращение звеньев. В качестве примера роботов с переменными линейными размерами звеньев отметим широко известные модели семейств роботов Unimate и Wersatran.

Перейдем теперь непосредственно к построению аналитических зависимостей, описывающих положение запястья W. Выберем в качестве базовой системы отсчета систему координат ^СХ₀, жестко связанную с плечевым шарниром S. Будем считать, что манипулятор находится в начальном состоянии, если θ₁ = θ₂ = ... = θ₇ = 0: манипулятор располагается строго вертикально, при этом каждое его звено занимает самое нижнее из всех возможных положений, а направляющая перемещения губок захвата при открытии-закрытии захватного устройства и ось вращения локтевого шарнира параллельны оси X.

Запишем матрицу преобразования, описывающую положение локтевого шарнира Е относительно базовой системы координат:

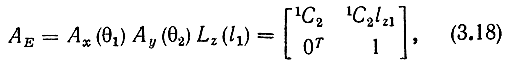
где А_х (θ₁), А_у (θ₂), А_z (θ₇) - матрицы преобразования координат, описывающие вращение на углы θ₁, θ₂, ..., θ₇, a L_z(l), L_z(l₂), L_z(l₃) - матрицы преобразования, описывающие параллельный перенос вдоль плечевого звена, локтевого звена и запястья. С учетом соотношения

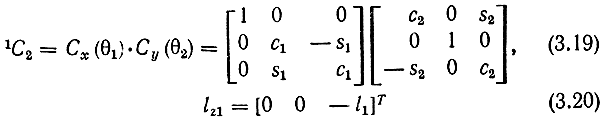
уравнение (3.18) может быть преобразовано к виду

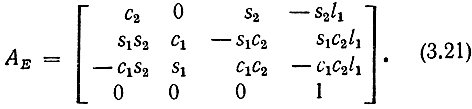
Сопоставляя матрицы A_E и B_total из (3.15), замечаем, что элементами позиций локтевого шарнира Е (х_Е, y_E, z_E) аналогично уравнению (3.16) являются три верхних элемента четвертого столбца матрицы (3.21), т. е.

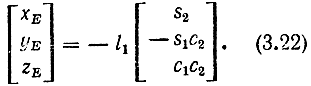
Аналогично строим матрицы преобразования для запястья:

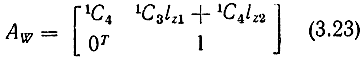
и захвата:

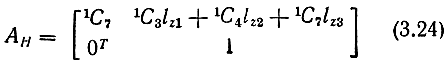
и сразу получаем искомую позицию запястья в виде

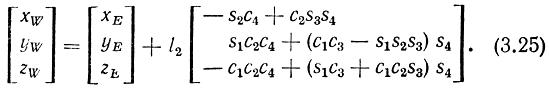
Алгоритм вычисления позиции и ориентации захвата, запястья и локтевого звена антропоморфного манипулятора при использовании векторного представления

Как уже неоднократно подчеркивалось, выражение (3.15) можно использовать для определения позиции и ориентации любых манипуляционных механизмов и их элементов, включая телескопические, или скользящие, соединения звеньев. Однако для ряда конструкций, и в частности для разработанного при участии автора этой книги робота MELARM, у которого три вращательные степени подвижности (θ₁, θ₂, θ₃) сосредоточены в плечевом шарнире S и еще три (θ₄, θ₅, θ₆) - в запястье W, непосредственное применение общего метода может потребовать хотя и простых, но довольно громоздких вычислений. Кроме того, представление информации в виде 4×4-матриц и 4-мерных векторов не позволяет выявить физический смысл задачи, что затрудняет проведение интуитивных рассуждений и анализа промежуточных результатов.

Для иллюстрации возможных подходов к вычислению положения сложных механизмов рассмотрим особенности применения 3-мерных векторов и 3×3-матриц на примере определения позиции и ориентации звеньев антропоморфного манипулятора MELARM-I^*.

^* (Применение векторных методов расчета для подобных конструкций существенно упрощает необходимые математические выкладки, что повышает наглядность решения. Кроме того, применение векторных методов позволяет продемонстрировать такие достоинства антропоморфного манипулятора MELARM-I, как простота решения задач кинематики (расчета положения), а следовательно, и легкость управления движением.)

В соответствии с рис. 3.33 имеем

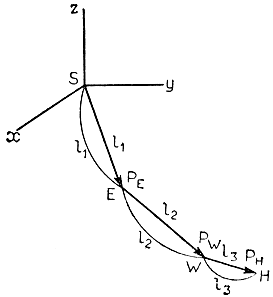
Рис. 3.33. Кинематическая схема манипулятора MELARM-I. Е - локтевой шарнир; W - запястье; Н - захватное устройство; P_Е, P_W, P_H - векторы позиции локтевого шарнира, запястья и захватного устройства

Для вычисления векторов l₁, l₂, l₃ поступим следующим образом. С помощью двух последовательных вращений на углы θ₁ и θ₂ вокруг осей х и у соответственно перейдем от исходной системы координат ^СХ₀ (x₀, у₀, z₀), жестко связанной с плечевым шарниром S, к новой системе ^СХ₂ (х₂, у₂, z₂) (рис. 3.34). Формально этот переход задается выражением

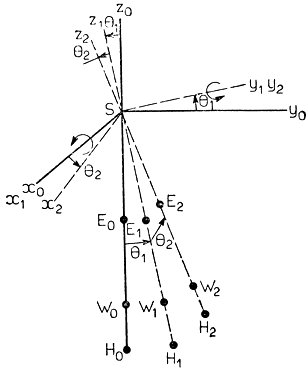
Рис. 3.34. Преобразование системы координат

В результате между координатами любой точки в новой системе координат ^СХ₂ и в старой системе координат ^СХ₀ имеет место соотношение

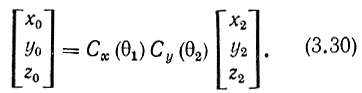
Точка E, связанная с локтевым шарниром, в исходном состоянии располагалась точно на оси z и имела координаты Е₀ (0, 0, -l₁). После двух переходов вида Е₀ → Е₁ → E₂, осуществленных в результате последовательных поворотов на углы θ₁ и θ₂, в новой системе координат ^СХ₂ координаты этой точки имеют прежние числовые значения Е₂ (0, 0, -l₁). Следовательно, можно записать

где С₁ и С₂ - сокращенная форма записи обозначений С_x (θ₁) и С_y (θ₂).

В результате поворотов на углы θ₁ и θ₂ исходная система координат ^СХ_Е0 с началом отсчета в точке Е₀ переходит в систему координат ^CX_E2, а после поворота плечевого звена на угол θ₃ и локтевого звена на угол θ₄ преобразуется в новую систему координат ^СХ₄. В ходе этих преобразований конец вектора l₂, совпадающий с точкой W, перемещается в точку W₄ (W₀ → W₂ → W₄), координаты которой совпадают с координатами точки W запястья в системе координат ^СХ₄. Так же как и в случае с точкой E, числовые значения координат точки W₄ совпадают с числовыми значениями координат точки W₀, соответствующей положению запястья W в исходной системе координат ^СХ_Е0. В обоих этих системах числовые значения координат точки W равны (0, 0, -l₂). Следовательно, справедливо выражение

Аналогично получаем следующее уравнение для вектора l₃, конец которого совпадает с точкой Н:

Если в этом уравнении заменить обозначения:

то окончательные выражения для искомых положений запястья и захватного устройства могут быть найдены в результате следующих преобразований;

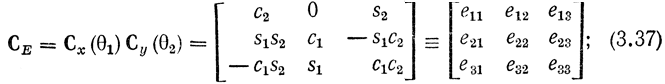
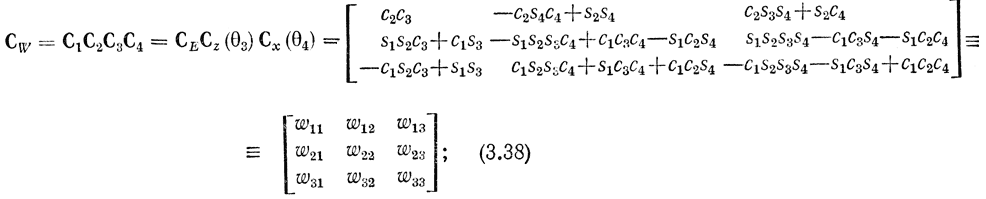
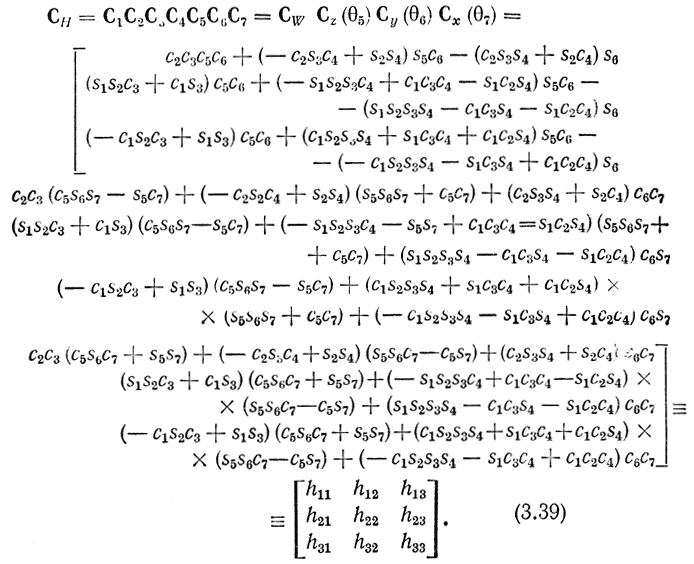
Исходя из уравнений (3.26)-(3.28) и (3.31)-(3.39), находим явные выражения для компонент векторов Р_Е, P_W и Р_Н, определяющих позиции локтевого звена Е, запястья W и захвата Н в неподвижной системе координат:

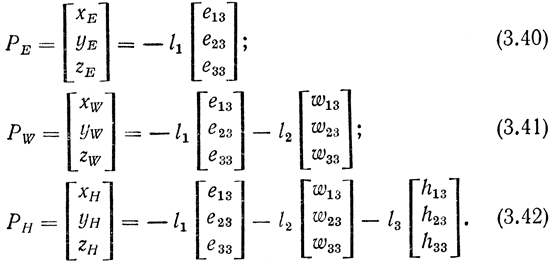
Очевидно, что числовые значения пространственных координат точек Е, W и H, полученные в результате вычислений по формулам (3.40)-(3.42), в точности совпадают с числовыми значениями, найденными при расчетах по формулам (3.22)-(3.25), которые были выведены с использованием 4×4-матриц преобразования. Однако, как и предполагалось, в случае антропоморфного манипулятора MELARM-I, применение аппарата трехмерных матриц и векторов привело к более простым и наглядным выкладкам по сравнению с непосредственными расчетами по полученным ранее соотношениям, основанным на представлении позиций и ориентации всех объектов в четырехмерном пространстве.

Методы расчета ориентации захватного устройства

Метод направляющих косинусов

Чтобы заставить манипулятор выполнить какое-либо задание, компьютеру, управляющему его работой, недостаточно одной лишь информации о текущей позиции некоторой связанной с захватным устройством точки: ему необходимо знать также и ориентацию захвата в рабочем пространстве.

Существует несколько универсальных методов расчета ориентации элементов многозвенных конструкций. Рассмотрим один из них. При этом будем полагать, что определить ориентацию захвата - значит, определить направления всех трех осей системы координат ^СХ_H, жестко связанной с захватным устройством (рис. 3.35). Для данной конструкции манипулятора связанная с захватом система координат ^СХ_H совпадает с системой ^СХ₇. Ориентация осей системы координат ^СХ_Н зависит от значений углов вращения по каждой из семи степеней подвижности θ₁, ..., θ₇. Рассматривая преобразование координат, состоящее из одних только вращений, получаем соотношение

где символ r[ ] указывает, что при выполнении преобразования учитываются только вращательные компоненты.

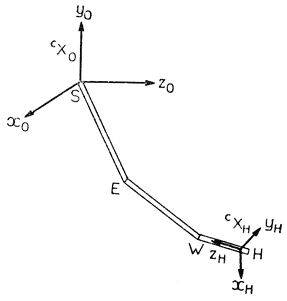
Рис. 3.35. Система координат ^СХ₀, жестко связанная с плечевым шарниром, и система координат ^СХ_Н, связанная с захватом

Если обозначить оси системы координат ^СХ_Н через х_Н, у_Н и z_H, а направляющие косинусы для оси х_H в системе координат ^СХ₀ через l_H1, m_H1 и n_H1 соответственно, то уравнение (3.43) примет вид

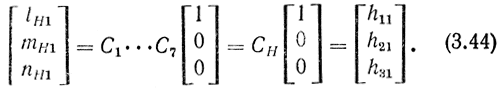
Аналогично, введя обозначения для направляющих косинусов осей у_Н и z_H в системе координат ^СХ₀ → l_H2, m_H2 и n_H2; l_H3, m_H3 и n_H3, получим

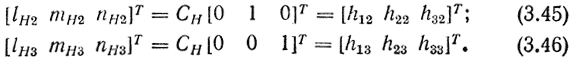
Уравнения (3.44)-(3.46) определяют матрицу направляющих косинусов К

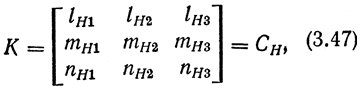
которая однозначно описывает ориентацию связанной с захватом системы координат ^СХ_n.

Таким образом, при использовании метода направляющих косинусов искомая матрица ориентации полностью совпадает с матрицей преобразования координат для трехмерного представления. Следовательно, если матрица преобразования С_Н известна, то для определения ориентации захвата не требуется никаких дополнительных вычислений, и в этом случае метод направляющих косинусов оказывается наиболее простым и удобным.

Метод явного представления углов ориентации захвата

Описание ориентации захвата с помощью матрицы направляющих косинусов очень удобно с вычислительной точки зрения. Однако информация, содержащаяся в этой матрице, практически ничего не говорит потребителю о том, какие все-таки углы составляет в данный момент захват манипулятора с осями неподвижной системы координат.

Воспользуемся для описания ориентации захвата непосредственно значениями самих углов. В качестве углов, характеризующих направление захвата в пространстве, выберем углы α, β и γ, которые в дальнейшем будем называть углами ориентации захвата. Физический смысл каждого из углов ориентации поясняется на рис. 3.36: угол α определяет величину отклонения захвата от правой вертикальной координатной плоскости неподвижной системы координат; угол β задает отклонение захвата от горизонтальной координатной плоскости той же системы координат, угол γ (или угол вращения захвата вокруг собственной оси) показывает величину поворота захвата в направлении вращения правого винта относительно исходного состояния, в котором направляющая перемещения губок захвата при сжатии-раскрытии оказывается параллельной оси X. Подобное представление ориентации захвата оказывается более наглядным и доступным для интуитивного анализа.

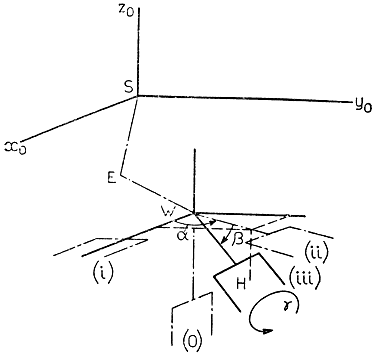
Рис. 3.36. Способ представления вектора ориентации захвата D_h (α, β, γ)

♦♦♦ Заметим, что введенные нами углы ориентации захвата имеют тот же физический смысл, что и углы Эйлера, используемые в физике для описания движения твердого тела.

Рассмотрим общую методику вычисления углов ориентации α, β, γ или захвата любого манипуляционного устройства. На

рис. 3.36 захват произвольного манипулятора представлен в четырех различных состояниях, одно из которых, помеченное (0), называется начальным. Сделав поворот на угол π/2 в правой координатной плоскости и поворот на π/2 вокруг своей оси, захват из начального состояния переходит в состояние i, занимая при этом горизонтальное положение. Затем в результате поворота на угол α в горизонтальной плоскости захват перемещается в состояние (ii). Далее, наклоняясь на угол β вниз от горизонтали и поворачиваясь вокруг своей оси на угол γ, он оказывается в состоянии (iii). Таким образом, результирующая матрица преобразования, описывающая полный, совершенный в результате перечисленных поворотов переход захвата из начального состояния в текущее (iii), представляется произведением матриц, описывающих каждый из поворотов в отдельности, т. е.

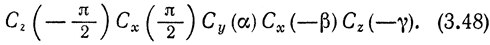
Выполнив умножение, получим следующие явные выражения для элементов результирующей матрицы вращения:

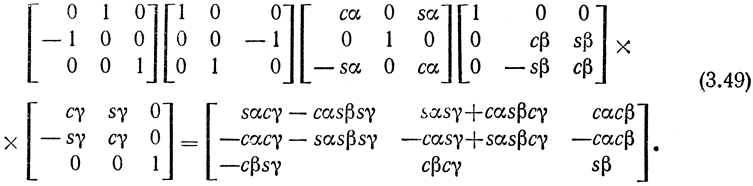
(Здесь sα и сα, sβ и cβ, sγ и сγ - тригонометрические функции - синусы и косинусы - углов поворота.)

До сих пор рассматривались возможные перемещения только одного звена n-звенного манипулятора, а именно захвата. Естественно, что на самом деле захват из начального состояния 0 попадает в текущее состояние только в результате некоторых перемещений по каждой из имеющихся степеней подвижности θ₁, ..., θ_n. Следовательно, результирующая матрица преобразования, описывающая текущее состояние захвата, является произведением матриц С₁ ... С_n, задающих перемещение по каждой из степеней подвижности θ₁, ..., θ_n в отдельности. Запишем это произведение в виде

Тогда с учетом матрицы, описывающей то же самое положение захвата в форме (3.49), имеем

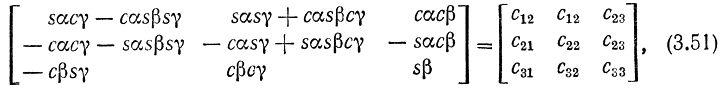
откуда непосредственно получаем следующие уравнения, позволяющие определить каждый из углов ориентации в отдельности.

Из уравнений (3.52) и (3.54) находим значение угла α:

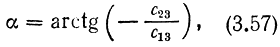
из уравнения (3.54) - значение угла β:

а из уравнений (3.55) и (3.56) - угла γ:

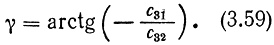
Таким образом, искомый вектор ориентации захвата D (α, β, γ) будет иметь вид

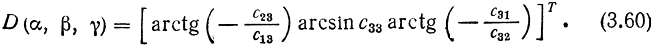
Поскольку при выводе соотношения (3.60) специально не оговаривались особенности конструкции манипулятора, оно оказывается справедливым для произвольных многозвенных манипуляционных механизмов. Например, для антропоморфного манипулятора MELARM-I входящие в уравнение (3.60) переменные с₁₃, c₂₃, c₃₃, c₃₁, с₃₂ совпадают с переменными h₁₃, h₂₃, h₃₃, h₃₁, h₃₂ в выражении (3.39). Если последние подставить в уравнения (3.37)-(3.59) вместо соответствующих универсальных обозначений, получим следующие значения углов ориентации захвата антропоморфного манипулятора MELARM-I:

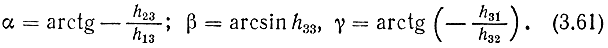
Методы расчета углов поворота каждого из звеньев для заданных позиций и ориентации захвата

До сих пор при рассмотрении процесса использования робота для выполнения какой-либо работы полагалось, что главным объектом управления является кисть робота, которая собственно и выполняла порученную работу. Теперь усложним задачу и определим положение всех звеньев манипулятора, которое в совокупности обеспечивает попадание захвата в заданную позицию с заданной ориентацией. При этом будем считать, что заданы положение рабочего объекта в пространстве и перечень манипуляций, которые требуется выполнить над рабочим объектом, и, кроме того, известны позиция и ориентация захватного устройства и момент взятия объекта.

Итак, по известному вектору позиции захвата Р_Н (х_Н, у_Н, z_H) и матрице ориентации захвата К требуется вычислить соответствующие значения всех углов θ₁, ..., θ₇.

Обратимся к рис. 3.37. На рисунке плечевому шарниру S сопоставлена неподвижная система координат ^CX₀, а с кончиком захватного устройства Н связана система координат ^CX₇, направление осей которой определяет ориентацию захвата относительно неподвижной системы координат. Обозначения l_H1, m_H3, n_H2 направляющих косинусов перепишем в форме l₁, m₃ и n₂ соответственно. В результате соотношение (3.47) примет вид

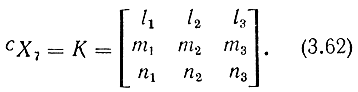
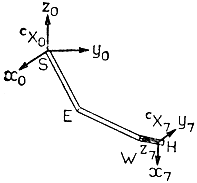
Рис. 3.37. Система координат, определяющая ориентацию захвата

Вместе с тем для антропоморфного манипулятора MELARM-I имеем

Умножив обе части уравнения последовательно на матрицы, обратные матрицам С₁, ..., С₄, получим

откуда найдем соотношения, характеризующие ориентацию запястья:

С учетом соотношения

из уравнений (3.65) - (3.67) получаем

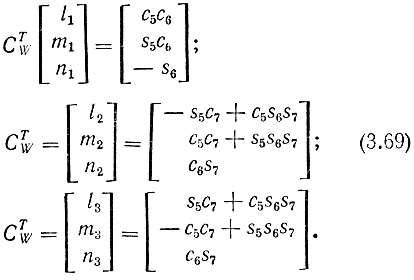
Решая систему данных уравнений относительно переменных, находим окончательные выражения для углов:

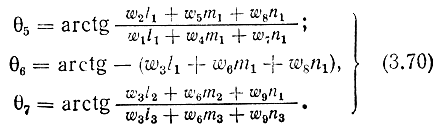
Теперь получим аналитические выражения для углов θ₁, ..., θ₄. Однако в отличие от задачи вычисления вектора позиции запястья манипулятора P_W по известным значениям углов θ₁, ..., θ₄ и длин звеньев l₁ и l₂ обратная задача^* не может быть решена однозначно. Дело в том, что каждая из трех известных компонент вектора позиции запястья x_W, y_W и z_W в общем случае зависит от всех четырех неизвестных значений углов θ₁, ..., θ₄. Естественно, что система из трех уравнений с четырьмя неизвестными не имеет однозначного решения.

^* (То есть вычисление значений углов θ₁, ..., θ₄, соответствующих данному положению захвата, когда вектор позиции запястья определяется известными значениями вектора позиции и матрицы ориентации.)

В рассмотренном примере появление неоднозначности обусловлено наличием у антропоморфного манипулятора семи степеней подвижности вместо шести минимально необходимых для достижения любой точки рабочего пространства. В подобных случаях говорят, что манипулятор обладает кинематической избыточностью.

Кинематической избыточностью, в частности, обладает рука человека. В самом деле, если одной рукой крепко взяться за цилиндрический стержень расположенный, как показано на рис. 3.38, то позиция и ориентация кисти запястья окажутся фиксированными, а вот локоть сохранит возможность покачиваться даже при неподвижном корпусе. В случае антропоморфного манипулятора с семью степенями подвижности избыточность также проявляется в возможности локтевого звена перемещаться по некоторой траектории, в то время как захват сохраняет неизменными заданные позицию и ориентацию. Не нарушая условий, наложенных на захват, локоть может находиться в любой точке, принадлежащей данной траектории. Следовательно, располагая лишь информацией о позиции и ориентации манипулятора с кинематической избыточностью, нельзя однозначно определить положение и ориентацию всех звеньев манипулятора (конфигурацию манипулятора) и, следовательно, управлять таким манипулятором.

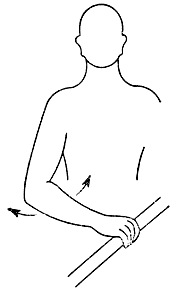
Рис. 3.38. Покачивание локтевого шарнира при неподвижной кисти, которая крепко обхватывает цилиндрический стержень

Вместе с тем, если бы удалось найти какой-либо достаточно простой способ управления избыточностью, то в нашем распоряжении оказался бы манипулятор, чрезвычайно гибкий по своим функциональным возможностям и обладающий очень широким диапазоном технологических применений. Например, с помощью руки человек может почесать за ухом, провести пальцем по спине, потянуться к предмету с противоположной от себя стороны, а также выполнять множество других сложных и разнообразных движений. И вся эта функциональная гибкость обусловлена наличием большой кинематической избыточности. Следовательно, решив задачу управления манипулятором, обладающим достаточным количеством избыточных степеней подвижности, можно с его помощью выполнять операции произвольной сложности.

Известны следующие основные подходы к расчету конфигураций избыточных манипуляционных устройств:

● выбор произвольной конфигурации, сохраняющей заданные позицию и ориентацию захвата. Для определенности вводятся какие-либо правила или критерии выбора, Например, критерий минимизации статической энергии манипулятора приводит к выбору конфигураций, в который локоть занимает самое низкое из возможных положений;

● выбор конфигурации в соответствии с некоторой заранее заданной определенной функциональной зависимостью переменных конфигурации (углов θ₁, ..., θ₇) от ориентации захвата;

● выбор конфигурации, исходя из особенностей выполняемых операций;

● выбор конфигурации, которая с учетом конструктивных особенностей манипуляционного механизма позволяет обеспечить наилучшую точность перемещения захвата в заданные позицию и ориентацию.

Из перечисленных подходов наиболее простым в реализации оказывается первый. Однако он практически не использует заложенные в избыточности преимущества, причем критерий минимума статической энергии неестественно сокращает зону обслуживания и диапазон перемещений захвата. Не вдаваясь в подробности практического использования второго подхода, отметим, что, как правило, применение данной группы методов сопряжено с большим количеством сложных вычислений. Третий подход обеспечивает выбор наиболее рациональной конфигурации манипулятора для каждого конкретного случая и поэтому является самым привлекательным с практической точки зрения. К сожалению, до сих пор исследования особенностей реализации такого подхода для современных промышленных роботов почти не проводились^*. Ниже обсуждаются наиболее простые методы, основанные на первом и последнем подходах.

^* (Автором книги разработаны методы практического использования первого, второго и четвертого подходов.)

Выбор конфигурации с наиболее низким расположением локтевого шарнира

Методика выбора конфигурации с наиболее низким из возможных расположением локтевого шарнира (конфигурация "нижайший локоть") иллюстрируется на рис. 3.39. Как показано на рисунке, продолжение отрезка E₀W, соответствующего локтевому звену, пересекается в точке F с вертикальной линией, проходящей через плечевой шарнир (ось Z). В этой конфигурации статическая энергия манипулятора имеет минимальное значение^*.

^* (Очевидно, таким подходом к выбору конфигурации не следует пренебрегать при управлении манипулятором с очень тяжелыми звеньями, а также во всех других случаях, когда особенно важно добиться минимального расхода энергии.)

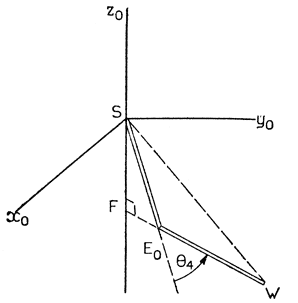
Рис. 3.39. Выбор конфигурации манипулятора по принципу 'нижайшего локтя'

Обозначим позицию, которую занимает локтевой шарнир в конфигурации "нижайший локоть", вектором

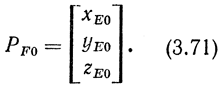
В этой конфигурации позиция запястья описывается изначально заданным вектором P_W = [x_W, y_W, z_W]^T. Анализируя рис. 3.39, получим следующие соотношения, характерные для конфигурации с минимальной статической энергией:

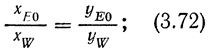
где R² - x_W² + y_W² + z_W². (3.76)

Из уравнений (3.22) и (3.36) с учетом приведенных соотношений (3.72)-(3.76) получим расчетные формулы для искомых переменных конфигурации - углов θ₁, ..., θ₄ вида

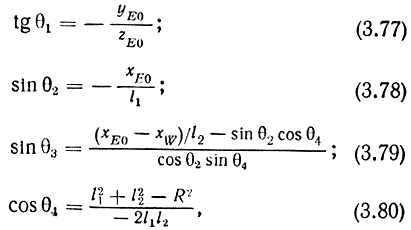
где

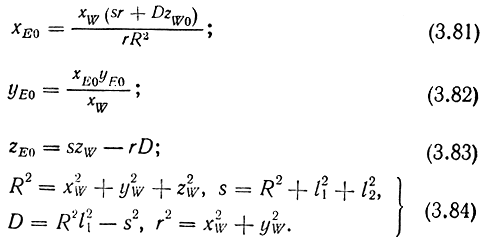
Таким образом, значения углов θ₁, ..., θ₄, обеспечивающие достижение конфигурации "нижайший локоть", определяются достаточно просто.

Выбор конфигурации методом явного указания позиции локтевого шарнира

Если внимательно понаблюдать за движениями руки человека в процессе выполнения им какой-либо работы, то нетрудно заметить, что ориентация кисти во многом определяется текущим положением локтевого шарнира, который совершает легкие покачивания вверх-вниз, обеспечивая наиболее удобное на данный момент положение руки. Чтобы определить положение локтевого шарнира в заданный момент времени, рассмотрим рис. 3.40, где Р_0е - точка пересечения прямой SW, соединяющей плечевой шарнир с запястьем, и плоскости, содержащей окружность С - траекторию всех возможных перемещений локтевого шарнира при фиксированном положении запястья. Изменяя расположение локтевого шарнира на окружности С, можно подобрать наиболее Удобную для каждого конкретного случая конфигурацию манипулятора. Поскольку такой подход обладает исключительной наглядностью, человек может явно указывать желаемое положение локтевого шарнира на окружности С.

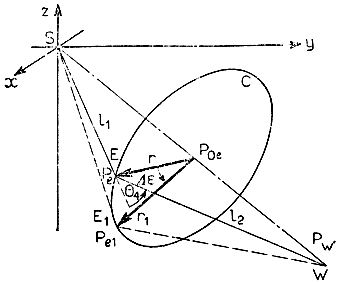
Рис. 3.40. Траектория, описываемая локтевым суставом

Определим переменные конфигурации θ₁, ..., θ₄ для случая явного задания положения локтевого шарнира. Допустим, что манипулятор перешел от текущей конфигурации к новой в результате смещения локтевого шарнира на угол Δε по окружности С. Зная величину Δε приращения угла ε, можно найти выражения для переменных конфигурации θ₁, ..., θ₃. В самом деле, если угол θ₃ задан, то в соответствии с рис. 3.39 имеем

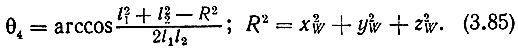
Отсюда с помощью выражений (3.40)-(3.42) находим углы θ₁ и θ₂:

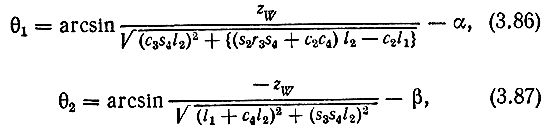
где

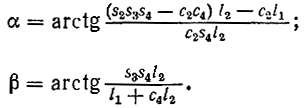
Кроме того, из рис. 3.40 следует, что

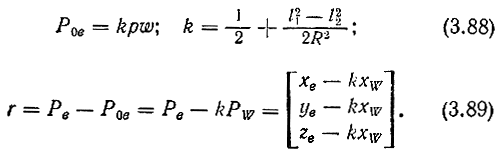
Считая, что вектор r при вращении на угол Δε переходит в вектор r₁, вычислим разность

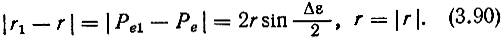
Таким образом, с помощью соотношений (3.89) и (3.90) всегда можно вычислить текущие значения переменных конфигурации.

Управление скоростью перемещения захвата

До сих пор речь шла о методах расчета конфигурации манипулятора, обеспечивающей заданное положение и ориентацию захвата при приближении к объекту манипулирования или в ходе выполнения манипуляций с этим объектом. При этом предполагалось, что направление движения захвата из исходного положения в заданное, а также скорость его перемещения могут быть найдены интуитивно по аналогии с действиями человека в подобной ситуации. Теперь перейдем к рассмотрению более строгих методов управления скоростью движения захватного устройства и звеньев манипулятора.

Один из наиболее универсальных и в то же время простых в реализации методов управления скоростью был предложен М. Уитни из Массачусетского технологического института (МТИ). Первоначально этот метод разрабатывался для расчета и управления скоростью движения каждого из звеньев манипулятора с шестью степенями подвижности (рис. 3.41), при условии что совокупное перемещение всех звеньев обеспечивает в каждый момент времени заданное значение вектора скорости движения захватного устройства. Полученный в результате способ расчета был назван Уитни методом раздельного управления скоростями^*. Рассмотрим особенности этого метода.

^* (Resolved motion rate control method.)

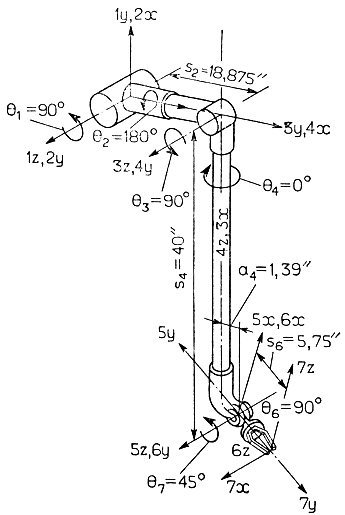
Рис. 3.41. Манипулятор с шестью степенями подвижности

Компонентами вектора скорости V перемещения начала координат системы координат, жестко связанной с текущим положением захвата (рис. 3.42), являются: R - скорость выноса руки вперед, L - скорость поднятия, S - скорость изгиба; три компоненты вектора вращения Ω представляют собой величины угловой скорости вращения вокруг каждой из соответствующих координатных осей системы координат захвата (кручения, поворота и качания). Все шесть компонент, описывающих скорости всевозможных перемещений захвата, в системе координат захвата представим в виде одного вектора скорости S:

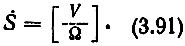
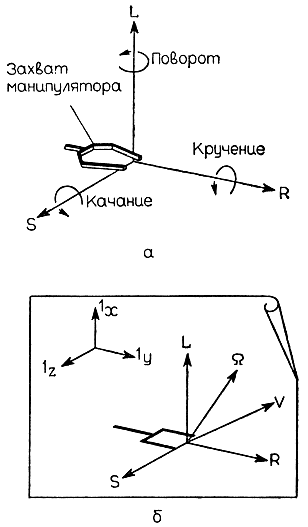
Рис. 3.42. Система координат захвата и вектор скорости движения захвата. а - расположение осей системы координат, связанной с захватом; б - векторы скорости движения V захвата и скорости вращения θ захвата

Введем вектор θ, компонентами которого служат текущие значения углов в каждом из шести шарниров манипулятора, и вектор θ, компонентами которого являются шесть значений скорости изменения величин углов в шарнирах. Тогда для вектора скорости захвата S и вектора скорости изменения углов в шарнирах θ имеет место следующее соотношение:

где J (θ) есть 6×6-матрица Якоби (якобиан). Из уравнения (3.92) находим зависимость угловых скоростей от скорости захвата:

Следовательно, зная численные значения всех величин, входящих в уравнение (3.92), и учитывая (3.93), можно получить искомые значения компонент вектора θ, обеспечивающие движение захвата манипулятора в заданном направлении с заданным значением вектора скорости S.

Рассмотрим подробнее способ вычисления якобиана J (θ). С каждым из шарниров манипулятора свяжем систему координат (рис. 3.43). Обозначив вектор скорости перемещения через V_j и вектор скорости вращения захвата через Ω_j при изменении угла θ_j только в одном j-м шарнире со скоростью θ_j (скорость изменения углов в остальных шарнирах равна 0), получим следующие соотношения:

где u_j - единичный вектор направления вращения на угол θ_j в шарнире j, a b_j7 - вектор, соединяющий начало системы координат, связанной с шарниром j (точка θ_j), и начало системы координат захвата (точка θ₇).

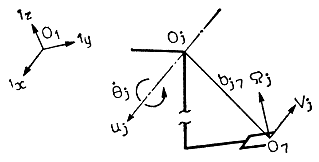
Рис. 3.43. Иллюстрация к методу вычисления якобиана J

Входящие в уравнения (3.94), (3.95) величины V_j и Ω_j определяют скорость движения захвата относительно неподвижной системы координат, связанной с плечом (система координат 1). Пусть матрица ¹С₇ есть 3×3-матрица преобразования, устанавливающая связь координат некоторой точки, заданных в системе захвата, с координатами этой же точки в системе 1. Учитывая, что ¹C₇^-1 = ¹C₇^T, можно написать выражения для скоростей V_j и Ω_j относительно системы координат захвата:

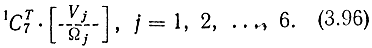
Исключая из вектора-столбца (3.96) величины θ_j (j = 1, 2, ..., 6), найдем зависимость скоростей движения захвата по всем возможным осям от изменения значения каждого из углов в шарнирах манипулятора с единичной скоростью. В результате с учетом уравнения (3.93) получим искомое выражение для якобиана J в виде

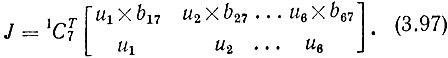
Наконец, определив матрицу, обратную матрице (3.97), и подставив ее в уравнение (3.93), найдем скорости изменения углов во всех шарнирах, которые в совокупности обеспечивают перемещение захвата в заданном направлении и с заданной скоростью. Однако общий объем вычислений, необходимых для расчета требуемых значений угловых скоростей, в соответствии с изложенным методом, оказывается достаточно большим, что осложняет организацию управления скоростью движения роботом в реальном масштабе времени. Для повышения скорости расчетов Уитни предварительно вычислил элементы матрицы J^-1, соответствующие некоторым определенным значениям углов отклонения каждого звена в положительном и отрицательном направлениях относительно нейтрального положения (всего 13 точек), а матрицу J^-1 для произвольной рабочей точки предложил находить интерполяцией известных значений J^-1 для ближайших фиксированных точек. По оценкам Уитни, точность управления при таком способе расчета якобиана J^-1 катастрофически ухудшается

Теперь рассмотрим применение изложенного метода управления скоростью для управления позицией манипулятора.

Пусть вектор b₁₇ (θ_i) определяет текущее положение начала отсчета системы координат, связанной с захватом, относительно начала отсчета системы координат 1, жестко связанной с плечевым шарниром манипулятора, а матрица ¹С₇ (θ_i) задает преобразование значений координат в системе 7 в соответствующие значения, выраженные в системе 1. Будем считать, что величины b₁₇ (θ_j) и ¹С₇ (θ_i), а также соответствующие величины b₁₇ (θ_j) и ¹С₇ (θ_i) для целевой точки известны. Последняя пара однозначно определяет положение и ориентацию целевого объекта, который должен быть захвачен манипулятором. Если предположить, что время, за которое захват переместится из текущего положения в целевое, равно Т, то нетрудно получить следующее соотношение между всеми введенными величинами:

При этом компонентами вектора V являются заданные в системе координат захвата скорости вытягивания, поднятия и изгиба захвата. Следовательно, вычисляя величину отклонения b₁₇ от исходного значения и преобразуя ее в системе координат захвата, согласно выражению (3.98), всегда можно вычислить скорость движения захвата. Аналогично можно записать соотношение, устанавливающее связь между вектором угловых скоростей и текущими значениями углов в шарнирах:

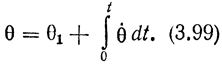
Расчет траекторий движения манипулятора

Расчет траекторий

Для каких бы операций ни использовался манипулятор, сущность выполняемой им работы сводится к последовательности перемещений захвата через некоторые специфичные для конкретного вида операций точки рабочего пространства, каждую из которых захват проходит в определенной ориентации, также обусловленной характером выполняемой работы. Следовательно, минимально необходимый набор функций системы управления манипулятором должен обеспечивать возможность вычисления для каждой рабочей точки значений углов в шарнирах манипулятора, соответствующих требуемым значениям позиции и ориентации захвата. Другими словами, система управления работой манипулятора должна справляться по крайней мере с решением таких задач, как:

● немедленное вычисление величины угла, на который должно повернуться каждое звено манипулятора, чтобы обеспечить требуемые позицию и ориентацию захвата;

● определение способа перемещения каждого звена манипулятора, обеспечивающего переход манипулятора из текущей конфигурации в целевую, определяемую значениями углов в шарнирах, которые были вычислены в результате решения первой задачи.

Несмотря на достаточно четкую формулировку исходных условий, решение любой из этих двух задач оказывается далеко не простым делом, особенно в случае многозвенных манипуляторов со сложной кинематикой.

Возможные подходы к решению первой из задач, т. е. методы вычисления углов во всех шарнирах манипулятора по заданным позиции и ориентации захватного устройства, были рассмотрены в предыдущих разделах данной главы. Теперь перейдем к методам управления перемещением всех звеньев манипулятора из текущей конфигурации в целевую. Наиболее тривиальным является метод, при котором движение по каждой из шести имеющихся степеней подвижности управляется отдельным сервоприводом, причем все вращения в шарнирах выполняются одновременно и независимо друг от друга. Однако при независимом управлении каждой степенью подвижности результирующее движение захватного устройства не обязательно окажется столь же плавным, как движение каждого звена. Кроме того, существует опасность, что в процессе перемещения захватное устройство или любая другая часть манипулятора может удариться о рабочий стол либо о другое препятствие, расположенное на пути из исходной конфигурации в целевую. Например, роботу требуется взять со стола какой-то предмет и поставить его на этот стол, но в другое место. В этом случае независимое управление степенями подвижности в соответствии с расчетными величинами изменения углов в шарнирах при переходе манипулятора из текущей конфигурации в конфигурацию взятия детали может привести к тому, что захват упрется в поверхность стола, не достигнув предмета, и дальнейшее движение всех звеньев будет заблокировано.

Чтобы избежать подобных ситуаций и гарантировать реализуемость перемещения в целевую конфигурацию, удобнее всего применять методы интерполяции траектории движения, которая заранее рассчитывается специальной программой. Компьютер разбивает эту траекторию на множество малых отрезков с помощью большого количества промежуточных точек, вычисляет для каждой промежуточной точки соответствующие значения всех углов в шарнирах и организует управление последовательным перемещением манипулятора от точки к точке до тех пор, пока захват не достигнет целевого положения. В этом случае, несмотря на то что поворот в каждом из шарниров на угол, соответствующий переходу манипулятора из одной конфигурации в соседнюю, по-прежнему может выполняться одновременно и независимо для всех шарниров, результирующее перемещение захвата оказывается более плавным.

Конечно, расчет соответствующих значений углов в шарнирах манипулятора при большом количестве промежуточных точек обычно требует значительных временных затрат. Количество промежуточных точек можно сократить, если заранее известно что в рабочей области робота нет препятствий, которые нужно обходить. При этом достаточно задать лишь несколько точек, обеспечивающих приемлемую плавность движения захвата. Один из примеров выбора промежуточных точек в среде с препятствиями и без препятствий приводится на рис. 3.45, где рассматриваются интерполяционные методы управления движением робота "Stanford Arm" с шестью степенями подвижности (рис. 3.44). Как следует из рис. 3.45, рабочая траектория помимо начальной и конечной точек должна включать в себя точку поднятия объекта над столом, которая находится неподалеку от начальной точки, и точку опускания объекта, расположенную вблизи целевой точки. Если существует опасность столкновения робота с препятствиями, то к этим точкам должно быть добавлено несколько дополнительных промежуточных точек, движение через которые гарантирует отсутствие столкновений. Таким образом, в общем случае рабочая траектория движения захвата определяется в результате плавного соединения узловых точек в следующей последовательности: начальная точка - точка вертикального подъема объекта - промежуточная точка - точка опускания объекта - целевая точка. Если для каждой узловой точки рассчитать соответствующие значения углов в шарнирах манипулятора и построить зависимости этих углов от времени, то в результате получаются достаточно плавные кривые, сходные по форме с кривой Пола, полученной им для одного из углов (рис. 3.45). Аналогичный вид будут иметь и зависимости от времени для любых других степеней подвижности. Следовательно, если каждый из шести сервоприводов будет реализовывать закон управления своим шарнирным углом в соответствии с приведенными зависимостями, то результирующее движение будет плавным как для захватного устройства, так и для любого звена манипулятора.

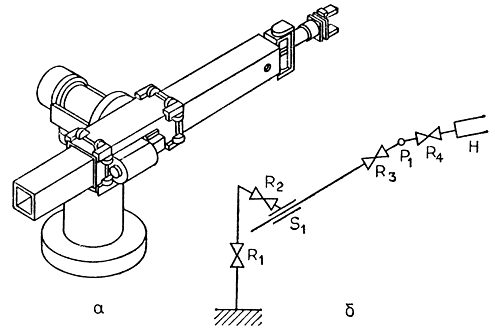
Рис. 3.44. Манипулятор 'Stanford Arm' с шестью степенями подвижности

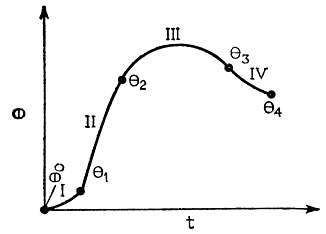
Рис. 3.45. Построение траектории перемещения захвата по узловым промежуточным точкам. θ₀ - исходная точка; θ₁ - точка вертикального подъема объекта; θ₂ - промежуточная точка (точка изгиба траектории); θ₃ - точка опускания объекта; θ₄ - целевая точка

Показанная на рис. 3.45 кривая проходит через три промежуточные точки и обычно описывается сложным алгебраическим многочленом высокого порядка, зависящим от одной переменной - времени. Чтобы понизить степень и упростить уравнение кривой, всю траекторию разбивают на несколько криволинейных отрезков достаточно простой формы. В частности, кривая на рис. 3.45 разбита на четыре части - I, II, III и IV. Условиями, определяющими характер движения на каждом отрезке, являются начальные и конечные значения координат (в данном случае величина угла θ), скоростей θ' и ускорений θ". Так, для начальной точки θ₀ отрезка I и для конечной точки θ₄ отрезка IV граничные значения скоростей и ускорений совпадают и равны 0. Во всех промежуточных точках кривой эти значения непрерывно изменяются при переходе от отрезка к отрезку в соответствии с изначальной формой кривой.

В рассматриваемом примере кривые на участках I и IV описываются многочленами четвертой степени от t, а криволинейные I отрезки II и III - многочленами третьей степени от t. Степень многочлена для первого участка обусловлена наличием следующих граничных условий: в начальной точке θ = θ₀ требуется, чтобы при t = 0 выполнялось равенство θ' = θ" = 0, а в конечной точке θ = θ₁ необходимо обеспечить непрерывность скорости θ' и ускорения θ" при переходе к следующему отрезку. Аналогично на участке II граничными условиями являются непрерывность функций θ' и θ" в каждой из точек θ₁ и θ₂, что приводит к алгебраическому уравнению кривой третьей степени. Степень многочленов, описывающих криволинейные отрезки III и IV, также определяется граничными условиями, которые имеют ту же структуру, что и для отрезков II, I.

Программируемые сервосистемы

Манипуляторы с программируемыми сервоприводами управляются непосредственно компьютером. Это означает, что для каждой степени подвижности в управляющем контуре сервосистем дополнительно предусмотрен компьютер со специальным программным обеспечением. В результате появляется возможность использовать компьютер для расчета необходимых корректирующих воздействий на приводы и, таким образом, возложить на программное обеспечение все заботы, связанные с повышением точности управления. Большая практическая ценность такого способа повышения точности привела к тому, что системы управления с компьютером в управляющем контуре были выделены в отдельный класс "программируемые сервосистемы" и сейчас находятся в центре пристального внимания исследователей и практиков.

В качестве примера, иллюстрирующего основные принципы работы программируемых сервосистем, рассмотрим представленную на рис. 3.46 систему управления приводами манипулятора с контуром компенсации ускорения.

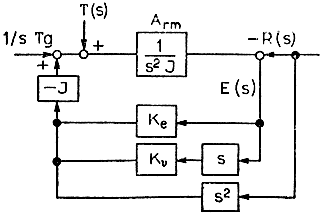
Рис. 3.46. Сервосистема с контуром компенсации ускорения. J - приведенный момент инерции; К_е, К_V - коэффициенты передачи в контурах обратной связи по позиции и по скорости; R(s) - целевое значение управляемой величины (ускорения); Т(s) - момент внешнего возмущающего воздействия; Tg - момент сил, обусловленных собственной массой манипулятора; Е(s) - отклонение манипулятора от заданной позиции

Для каждой степени подвижности приведенный момент инерции J существенно изменяется при изменении конфигурации всего манипулятора. Однако если с помощью компьютера непрерывно вычислять величину J для текущей конфигурации манипулятора и полученное значение умножать на коэффициент передачи сервосистемы, то оказывается, что значение управляющего воздействия, вырабатываемое сервосистемой без контура компенсации, можно поддерживать постоянным независимо от текущей конфигурации манипулятора. Далее, момент сил Tg, обусловленный собственной массой манипулятора, является главной составляющей суммарного момента Т(s) возмущающих воздействий и также существенным образом зависит от конфигурации манипулятора. Поэтому, если вычислять с помощью компьютера величину изменения момента силы собственной массы и добавлять ее к отрицательной величине суммарного момента силы тяжести, то влияние силы тяжести станет почти незаметным и, кроме того, уменьшится значение постоянного отклонения захвата от заданной точки позиционирования. Наконец, можно провести еще одно усовершенствование сервосистемы, если вычисление первой и второй производных многочленов 3-4-й степени, полученных при построении кривой, осуществлять непосредственно в контуре управления (рис. 3.46).