5.2. Регулирующие предикаты

Слово предикат означает то же, что условие. Термин этот принят в математической логике. Введенные нами логические операции (см. § 2.7) проверяют выполнение условий или, как говорят в логике, определяют логическое значение предиката.

Описывая ниже алгоритмы, совместно преобразующие один общий операнд, сущность используемых при этом приемов будем пояснять с помощью семантических схем. Для операторных алгоритмов эти схемы будут отражать и их структуру. Для записи семантических схем используем язык схем, введенный в § 4.8. Характер этой книги вынуждает меня вместо строгих доказательств ограничиться содержательными рассуждениями и примерами.

Как одно из средств координации алгоритмических процессов нам потребуется один тип операции, который мы сейчас объявим.

Пусть, 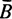- некоторая буферная подконструкция операнда. Обозначим через 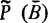логическую локальную операцию, проверяющую, обладает ли В некоторым свойством. Можно построить первичный алгоритм, состоящий из одного условного приказа:

1) Если 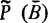, то стоп, иначе → 1;

Этот алгоритм осуществляет тождественное преобразование буфера 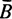, если он удовлетворяет условию 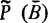, и неприменим к нему в противном случае. Отображение, реализуемое этим алгоритмом, объявим операцией и назовем ее "Ожидать 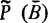". В составе одиночного первичного алгоритма приказ, например, вида

5) Ожидать 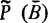, → 6 ;

не влиял бы на алгоритмический процесс, если условие 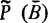выполняется; в противоположном случае он вызывал бы безрезультатную остановку. Другое дело, если этот приказ входит в состав одного из алгоритмов, совместно перерабатывающий общий операнд. Остановка длилась бы до тех пор, пока один из других алгоритмов не преобразовал бы В так, что условие 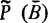выполнится. Отмечу, что для выполнения операции "Ожидать 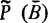" нужно читать подконструкцию 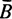или ее часть, но не нужно ничего писать.

Рассмотрим теперь случай, когда n алгоритмов А₁, А₂, ... , А_n обрабатывают операнд, в котором подконструкция 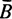является буфером, доступным для любого из этих алгоритмов. Предположим, что существуют п предикатов 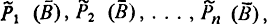удовлетворяющих следующим двум условиям:

1. для любого состояния 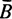эти предикаты определены;
2. всегда только одно условие выполняется, а все остальные не выполняются.

Такую совокупность условий будем называть системой регулирующих предикатов n-го порядка.

С помощью системы регулирующих предикатов n-го порядка можно обеспечить бесконфликтное обращение алгоритмов к буферу 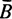, если число алгоритмов не более n. Проиллюстрирую это на частном примере, когда n = 3. Пусть семантические схемы алгоритмов имеют вид:

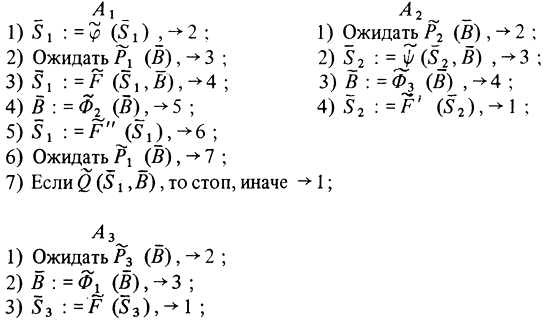
В этих схемах алгоритмов 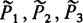- система регулирующих предикатов 3-го порядка. Преобразование 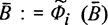так перерабатывает В, что становится выполненным условие 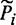, где i = 1, 2 или 3. Смысл остальных функциональных и предикатных знаков понятен (в нужной степени) из текста схем; 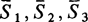- собственные подконструкции алгоритмов.

Защитой от конфликтов являются операции "Ожидать". Только в приказах, которые следуют за приказами, содержащими эту операцию, могут стоять приказы, обращающиеся к буферу, и последним по порядку выполнения является приказ, изменяющий так состояние буфера, что право обращения к нему получает один из остальных алгоритмов. Регулирующие предикаты взаимно-однозначно соответствуют алгоритмам. В принципе, число алгоритмов может быть меньше порядка системы регулирующих предикатов. В этом случае взаимно-однозначное соответствие должно существовать между множеством алгоритмов и некоторым подмножеством регулирующих предикатов.

Если внимательно проследить за процессом выполнения алгоритмов, то можно заметить, что каждый алгоритм может разрешать обращение к буферу другому, запрещая такое обращение себе. При этом нужно иметь в виду, что алгоритмы могут иметь условные приказы, которые приводят к разветвлению процесса выполнения данного алгоритма и могут иметь циклический характер, при котором происходит возврат к уже выполненным один или несколько раз приказам. В процессе выполнения каждого алгоритма до обращения к буферу должна быть обеспечена невозможность одновременного обращения к буферу другого алгоритма. Она обеспечивается тем, что обращению к буферу предшествует (хотя, может быть, не непосредственно) приказ ожидания.

На рис. 5.1 схематически показан совокупный процесс выполнения алгоритмов А₁, А₂, А₃ в предположении, что начальное состояние буфера 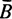удовлетворяет условию 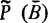и что при повторном выполнении приказа 7 первого алгоритма реализуется отсылка "стоп". На рисунке в горизонтальных строках записаны номера выполняемых приказов, причем номера приказов ожидания заключены в скобки, а после номеров приказов, изменяющих состояние буфера, в скобках указаны номера алгоритмов, которым эти приказы разрешают обращаться к буферу. Анализируя схему совместного процесса, замечаем, что конец выполнения приказа, разрешающего обращение к буферу, является также концом выполнения приказа об ожидании, стоящего в некотором другом алгоритме. Процесс оканчивается остановкой первого алгоритма, влекущей за собой вход других алгоритмов в бесконечное ожидание. Тем не менее считается, что совокупный процесс заканчивается результативно, так как составитель алгоритмов это заранее предвидел (если, конечно, он не допустил ошибки).

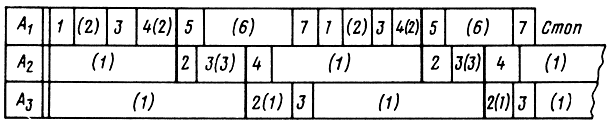
Рис. 5.1. Схема совместного выполнения трех алгоритмов, имеющих регулируемый буфер

Если бы одна и та же группа совместно работающих алгоритмов пользовалась не одним, а двумя буферами (каждый со своей системой регулирующих предикатов), то существовала бы возможность того, что все алгоритмы впадут в ожидание и процесс остановится без того, чтобы хотя бы один алгоритм достиг отсылки типа "стоп". Это явление называют схватыванием, или клинчем. При разработке алгоритмов его предусмотреть или исключить трудно, и оно считается нежелательным. Но простейшие примеры схватывания привести легко.

Рассмотрим опять три алгоритма; пусть 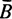₁ и 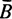₂ - две буферные подконструкции, причем первая связана с регулирующими предикатами 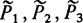, а вторая - с регулирующими предикатами 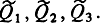Предположим, что первый алгоритм начинается с приказа

1) Ожидать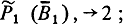

второй - с приказа

1) Ожидать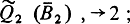

а третий - с приказа

1) Ожидать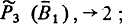

Пусть, кроме того, начальное состояние буферов таково, что для них выполняются условия 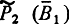и 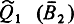Ясно, что все три алгоритма сразу же впадут в бесконечное ожидание, т. е. наступит схватывание.

Заметим, что если бы начальное состояние буферов было таково, что выполняются условия 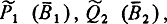то схватывания при выполнении первых приказов не произошло бы. А дальнейшие приказы могут благоприятно изменить состояние буферов.

О любых нескольких алгоритмах, имеющих общий буфер, принято говорить, что они связаны этим буфером. О системе предикатов n-го порядка, регулирующих обращения к буферу 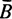, говорят, что она задана на этом буфере, как и каждый регулирующий предикат. Если в семантической схеме алгоритма А, связанного буфером 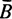, присутствуют приказы "ожидать 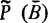", то про алгоритм А и предикат 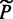говорят, что они соответствуют друг другу.

Мы рассматриваем достаточно общий случай, когда каждому алгоритму, соответствует только один из регулирующих предикатов, заданных на буфере .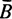

Существуют два очень важных вида связи между алгоритмами и регулирующими предикатами:

1. Каждому из n предикатов, регулирующих обращение к буферу 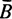, соответствует хотя бы один алгоритм. В этом случае буфер 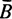называется закрытым.
2. Лишь некоторым из n регулирующих предикатов, заданных на буфере 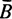, соответствуют алгоритмы из числа перерабатывающих совокупный операнд. В этом случае буфер 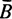называется открытым.

Каждый из этих случаев допускает два варианта:

1. соответствие между регулирующими предикатами и алгоритмами (если оно существует) является взаимнооднозначным;
2. некоторым предикатам соответствует несколько алгоритмов.

Соответствие "алгоритм - предикат" однозначное, а "предикат - алгоритм" не однозначное.

Два (или более) алгоритма, соответствующие одному и тому же предикату, называются сопряженными относительно указанного предиката.

Открытые буферы позволяют вводить в операнд, в то время когда ни один алгоритм к этим буферам не обращается, воздействия из внешней среды.

Ясно, что в теории роботов открытые буферы играют существенную роль. Кроме того с их помощью можно обеспечить "одновременный" запуск нескольких алгоритмов. Например, представим себе, что в начале каждого из трех алгоритмов, приведенных на с. 83, стоял бы приказ следующего вида:

0) Ждать 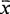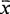= 1 , →1 ;

где 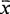- некоторая подконструкция (буфер), которая может принимать одно из двух значений: 0 или 1. Равенство 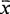= 1 является регулирующим предикатом, который вместе с предикатом 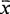= 0 образует систему второго порядка. Буфер 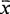является открытым, и все три алгоритма были бы сопряженными относительно предиката 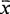= 1. Все три алгоритма постоянно находились бы в состоянии ожидания предиката 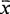= 1, и как только человек, который по отношению к совокупности алгоритмов является частью внешней среды, произведет действие 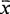= 1 ; все алгоритмы одновременно станут выполняться. Отсылка "стоп" может быть заменена отсылкой к приказу вида

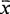100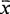) : = 0, →0 ;

и, таким образом, остановка алгоритма будет реализована как ожидание предиката "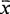 = 1". К анализу описанных применений открытых буферов мы еще вернемся.