6.1. Алгоритмически неразрешимые проблемы

Прежде всего заметим, что когда идет речь о разрешимости или неразрешимости проблем, то имеются в виду не одиночные проблемы, а массовые. Примером одиночной проблемы может служить задача: "Найти сумму чисел 2 и 3". Массовые проблемы требуют нахождение некоторого общего метода или алгоритма. Например, массовой проблемой является задача: "Найти алгоритм получения суммы двух произвольных целых чисел x и y". Такой алгоритм нам известен "со школьной скамьи". Обе названные проблемы разрешимы, причем, имея решение массовой проблемы, мы без труда решим и входящую в нее одиночную проблему.

Неразрешимыми могут быть как одиночные, так и массовые проблемы. Например, неразрешимая одиночная проблема: "Найти частное от деления числа 3 на число 0". Соответствующая массовая проблема: "Найти алгоритм для получения частного от деления произвольного числа х на число 0". Эта проблема тоже неразрешима, но такие массовые проблемы, которые являются совокупностью неразрешимых одиночных проблем, не удивительны. Однако при исследовании феномена неразрешимости рассмотрение и таких проблем может принести пользу.

Рассмотрим еще одну массовую проблему. Предположим, что нам дано конечное множество символьных конструкций, каждой из которых присвоено имя. Для простоты будем считать, что имена являются словами. Список имен, разделенных запятыми, будем называть каталогом. Каталог - тоже символьная конструкция, и мы будем его тоже снабжать именем. От имен требуется, чтобы они были попарно различны между собой. Например, имеются три конструкции и их именами являются строчные буквы русского алфавита "а", "б" и "в". Обозначим отношение именования (х есть имя конструкции К) знаком ":: =", который мы прежде употребляли в метаформулах, вкладывая в него несколько иной смысл. Тогда можно написать

Эта запись означает, что каталог, содержащий имена двух символьных конструкций, указанных справа, сам имеет имя "k₁". Построим еще один каталог

Этот каталог содержит свое собственное имя. Составляя каталоги, мы расширяем изучаемое множество именованных символьных конструкций. Не будем составлять слишком много каталогов, так как основных символьных конструкций у нас всего три и каталоги будут главным образом упоминать в своем составе друг друга. Допустим, что нами всего составлено три каталога: два ранее указанных и каталог

Каталоги, упоминающие самих себя, назовем автонимными, а не упоминающие себя - неавтонимными. Предположим, что требуется составить еще один, последний каталог k₄, который должен быть каталогом всех неавтонимных и только неавтонимных каталогов.

Казалось бы, построить каталог k₄ нетрудно. Он будет

Стоп! Это неверно, потому что он сам себя не упоминает и, значит, не является каталогом всех неавтонимных каталогов. Исправим его:

Теперь он сам себя упоминает и потому перестал быть каталогом только неавтонимных каталогов. Что же, проблема неразрешима? Да, неразрешима! Но почему? Да потому, что мы требуем от к4 невозможного: по нашему требованию, если он себя не упоминает, т. е. неавтонимен, то должен по этой причине себя упоминать; если же он себя упоминает (и, значит, автонимен), то должен не упоминать. В обоих случаях он должен одновременно и упоминать и неупоминать себя. Такое условие называется абсурдным. Каталог k₄абсурден и потому невозможен.

В нашем примере проблема каталога k₄ была одиночной. Но если бы множество исходных конструкций было произвольным конечным, то можно было бы поставить массовую проблему нахождения алгоритма построения каталога всех неавтонимных и только неавтонимных каталогов. Она, понятно, была бы неразрешима.

Видоизменим проблему каталога так, чтобы она была проблемой, связанной с алгоритмом. Рассмотрим класс алгоритмов, записи которых являются словами в алфавите 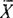, и в качестве допустимых исходных данных могут иметь любые слова в алфавите 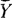, содержащем не менее двух букв. Любую запись алгоритма нашего класса можно закодировать в виде слова в 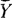. Действительно, если буквами алфавита Y являются "а", "б", ..., то можно 1-ю букву алфавита 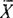закодировать в виде слова "аба", вторую в виде слова "абба", третью - в виде слова "аббба" и т. д. Такой код является однозначным и, более того, однозначным в обе стороны. Если какой-либо алгоритм применим к коду другого алгоритма В, то назовем его применимым к В, если же он применим к своему коду (описанного вида), то будем его называть самоприменимым. Если алгоритм не применим к своему коду, то будем его называть несамоприменимым. Рассуждая так же, как с каталогами, мы без труда докажем, что алгоритм, применимый ко всем несамоприменимым и только к несамоприменимым алгоритмам и принадлежащий нашему классу - абсурден. Это еще одна неразрешимая проблема - построение такого алгоритма.

Читатель скажет, что в этом примере нет ничего нового... Но погодите! Рассмотрим теперь вопрос о разрешимости проблемы распознавания несамоприменимости. Предположим, что она разрешима, т. е. известен алгоритм, имеющий схему:

где 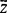- произвольный код алгоритма; 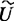(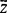) - процедура распознавания несамоприменяемости; 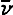- ответ.

Но тогда можно построить алгоритм

1) Если 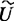(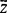), то стоп, иначе → 1;

Применение этого алгоритма к коду несамоприменимого алгоритма, не изменяет этот код, а применение к коду самоприменимого - приводит к зацикливанию, что означает неприменимость. Другими словами, мы получили алгоритм, который применим ко всем несамоприменимым и только к несамоприменимым алгоритмам, т. е. мы пришли к абсурду. Все это справедливо, если последний алгоритм принадлежит к нашему классу. При таком условии мы должны признать, что процедура распознавания несамоприменимости не существует. Задача распознавания несамоприменимости оказалась неразрешимой массовой проблемой.

Но тогда неразрешима и проблема распознавания самоприменимости, так как она тесно связана с проблемой распознавания несамоприменимости...

Наше доказательство условно справедливо. Если допустить гипотезу, что для всякого алгоритма, имеющего в качестве исходных данных слова в 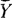, существует эквивалентный ему алгоритм в указанном нами классе (и если эта гипотеза будет верна!), то доказательство становится завершенным.

Смысл и правомерность такой гипотезы мы обсудим чуть позже, а сейчас вернемся к рассмотренной нами массовой проблеме. Итак, массовая проблема распознавания самоприменимости алгоритмически не разрешима. Но в ее состав входят одиночные проблемы, которые разрешимы. Например, натуральные алгоритмы, в которых не применяются операции линеаризации и делинеаризации (см. § 4.4), принадлежат нашему классу алгоритмов. Имея тот или иной натуральный алгоритм, можно его закодировать и непосредственно применить его к своему коду. К примеру возьмем алгоритм

1. *, 2 ;
2. →, 3 ;
3. ×, стоп ;

Читатель, если он не верит мне на слово, может убедиться, что этот алгоритм самоприменим.

Значит, существуют массовые проблемы, которые неразрешимы, тогда как входящие в их состав частные проблемы могут быть разрешимыми.

Если неразрешима проблема самоприменимости, то можно сказать, что неразрешима и проблема распознавания применимости произвольного алгоритма нашего класса к произвольному допустимому для него исходному данному. Это следует из того, что, имея алгоритм распознавания применимости любого алгоритма к любому допустимому для него исходному данному, мы сумели бы составить алгоритм распознавания самоприменимости, что в действительности невозможно.

Обсудим вопрос об упомянутой выше гипотезе. Поразительно, но факт, что такая гипотеза принята в логической теории алгоритмов. В разных разделах логической теории алгоритмов она известна под разными названиями и формулируется в различном виде. Тезис Черча, тезис Тьюринга, принцип нормализации - вот ее разные формы и названия. Она не является ни теоремой, ни аксиомой, потому что связывает не формализованное в логической теории алгоритмов понятие алгоритма вообще с понятием алгоритмов довольно узкого класса, которое сформулировано строго. Это нечто вроде принципа (закона) сохранения материи.

Доказать справедливость такого принципа нельзя, но по мнению ряда математиков он подтверждается всей практикой человечества. Они говорят "Попробуйте его опровергнуть!" Читатель согласится, что для математики, если считать ее наукой, имеющей особенный метод, такое явление необычно. Но в том то и дело, что математика, хотя она и очень абстрактна, является одной из естественных наук и, нравится это или нет некоторым идеалистам, почитающим себя знатоками оснований математики, ее основанием является совокупная практика человечества.

Замечу, что аналитическая теория алгоритмов дает широкое формальное определение алгоритма, по отношению к которому все логические теории алгоритмов являются теориями частных семейств алгоритмов. При более широком, необходимом для практики понятии алгоритма можно было бы вышеназванные тезисы доказать для алгоритмов, исходные данные и результаты которых являются словами. Хотя эти доказательства еще не проведены, но я думаю, что их можно сделать. Что же касается алгоритмов, перерабатывающих более сложные (чем слова) конструкции, то для них, конечно, эквивалентов вышеуказанного частного класса может не быть.

Иногда приходится слышать утверждение, что неразрешимость массовых проблем связана с их слишком большой общностью. Стоит сузить проблему надлежащим образом, и она станет разрешимой. Но что значит "сузить"? Если ее сузить до одиночной проблемы, то, как я показал выше, она может стать разрешимой. Но доказано, что и одиночные проблемы бывают неразрешимы. Значит, причина неразрешимости не в обширности проблемы, а в ее особенностях. Если проблему сузить так, чтобы ее "плохие" особенности были устранены, то получится подпроблема данной проблемы, которая разрешима. Решить вопрос о том, как произвести такое сужение - сложная математическая задача. Но для практических целей это и не нужно. Поясню сказанное примером.

Вернемся к самому первому и безнадежному случаю. Построить каталог всех неавтонимных и только неавтонимных каталогов невозможно. Но зачем нам такой каталог? Вероятно, для того чтобы по нему находить неавтоним-ные каталоги. Если, строя каталог каталогов, мы будем помечать, какие из них автонимные, например, пометкой "(-)", то каталог, упоминающий все неавтонимные каталоги, будет пригоден для нахождения неавтонимных каталогов. А чтобы не затруднять работу, связанную с поиском в каталоге, будем строить минимальный каталог, содержащий имена всех неавтонимных каталогов. В нашем случае это будет (см. с. 98):

Отсюда вывод: сталкиваясь с неразрешимой проблемой, мы должны вместо нее искать разрешимую, которая решает нужные нам задачи. Во многих случаях простой здравый смысл подскажет нам, как это сделать. Во всяком случае феномен неразрешимости является существенным препятствием для составления многих алгоритмов и заслуживает самого пристального внимания.

Феномен неразрешимости обнаружен логической теорией алгоритмов. Однако неразрешимые проблемы существуют и для аналитической теории алгоритмов, в рамках которой мы действуем, потому что классы алгоритмов, используемые в логической теории алгоритмов, являются частными случаями алгоритмов в широком смысле.

При этом можно утверждать, что любой алгоритм, изучаемый в аналитической теории, либо эквивалентен некоторому из избранных алгоритмов (изучаемых в логической теории), либо ему равносилен. Под равносильностью понимается следующее. Если алгоритм А перерабатывает операнд X в результат Y и если избранный алгоритм В, могущий перерабатывать только слова и слова-результаты, перерабатывает^*l (X) в некоторый у, причем d (y) = Y, то говорят, что А равносилен В. Другими словами, основная гипотеза, которая была нами названа выше, по отношению к алгоритмам аналитической теории является просто доказанной теоремой.

^* (Напоминаю, что l означает линеаризацию, а d - делинеаризацию.)

Зададимся теперь вопросом: как понимать феномен неразрешимости в общечеловеческом и философском смысле? Существуют ли неразрешимые проблемы для человека?

Совершенно ясно, что машине решение произвольной одиночной проблемы, входящей в неразрешимую массовую проблему, не под силу. Ведь программы - это алгоритмы, а неразрешимая проблема потому и неразрешима, что алгоритма, пригодного для любой одиночной проблемы, нет. Некоторые ученые говорят, что человек тем и отличается от машины, что любую одиночную проблему, входящую в неразрешимую проблему, он может решить [13]. Такое категорическое заявление - ошибочно.

Если одиночная проблема не разрешима, то она подобна задаче: "Найди число, которое меньше чем 1 и больше чем 2". Такая проблема не разрешима ни для машины, ни для человека. Если же одиночные проблемы все разрешимы, но нет общего алгоритма для решения любой из них (массовая проблема не разрешима), то его нет ни для машины, ни для человека. И тогда нужно искать разрешимую массовую проблему, которая охватывает только случаи, имеющие практическое значение. Но тогда алгоритмы будут существовать и для машины и для человека. Человек сможет и решить любую одиночную проблему, и составить программу для машины.

Некоторые "философы", стремясь опровергнуть материалистическую диалектику, говорят, что феномен неразрешимости доказывает непознаваемость мира. Но им могут поверить только те, кто не знает, что такое феномен неразрешимости. Скорее, этот феномен подтверждает, что на некоторых языках можно высказать формулировки, которые кажутся осмысленными, но в действительности бессмысленны. Вроде утверждения "данная фраза ложна". Почему-то такие философы не удивляются тому, что нет общей грамматики для всех языков мира, а вот отсутствие общего правила для определения несамоприменимости алгоритмов их наводит на мысль о непознаваемости мира.

Отмечу одну особенность массовых проблем. Если они объединяют в себе конечное множество разрешимых одиночных проблем, то они всегда разрешимы, сколь бы велико не было число одиночных проблем. Тому доказательством является принципиальная возможность построения таблицы решений. Но для очень больших множеств (хотя и конечных) таблица решений будет практически бесполезной. Массовая проблема, объединяющая бесконечное множество разрешимых одиночных проблем, может оказаться неразрешимой.

Так как в дискретном роботе число всевозможных комбинаций символов, порождаемых рецепторами, конечно, то и число возможных состояний его "памяти", а значит, и число могущих возникнуть одиночных проблем тоже конечно. Значит, массовая проблема, объединяющая все эти одиночные проблемы, должна быть алгоритмически разрешима.