2. Исчисление предикатов как язык робота

... Ни в какой интеллектуальной проблеме 
не следует пренебрегать логикой.

С. Клини

Для автоматизации процессов постановки и решения интеллектуальных задач роботу необходим адекватный язык. Этот язык должен служить не только и не столько средством представления знаний (информации), сколько средством логического анализа интеллектуальных задач.

Обычные человеческие языки, развивавшиеся под влиянием практических потребностей простоты общения (что далеко не всегда совместимо с точностью и надежностью логического анализа!), для этой цели плохо подходят. По этой причине желательно, даже практически необходимо использовать в качестве языка робота специально созданный формализованный язык. Такой язык в противоположность обычному языку должен следовать за логической формой и воспроизводить ее даже в ущерб краткости и легкости общения, если это будет необходимо. Главной отличительной чертой такого формализованного языка является наличие в нем особой системы логического вывода или дедукции.

В качестве языка робота, удовлетворяющего указанным требованиям, мы возьмем исчисление предикатов. В терминах исчисления предикатов можно сформулировать многие предложения и утверждения, выраженные на естественных языках, а также формализовать процесс рассуждений и доказательств. Благодаря этому может быть устранен или во всяком случае резко снижен "языковый барьер" между роботом и человеком.

Для того чтобы описать исчисление предикатов, мы должны воспользоваться какой-то частью обычного языка и в терминах этого языка образовать словарь и сформулировать правила формализованного языка, включая правила логического вывода. Исчисление предикатов (точнее, его синтаксис и семантика) определяется следующим очень экономным словарем символов и правилами их соединения и интерпретации:

1. Имена. Это - заимствованные из обычных языков выражения, служащие для непосредственного обозначения предмета. Примерами имен являются: "роботы", "мозг", "манипулятор", "Юнимейт", "источник энергии", "искусственный интеллект" и т. д.

Интересно отметить, что в одном или различных языках разные имена могут быть синонимами и выражать один и тот же смысл. С другой стороны, одно имя в различных языках или даже в одном языке (при омонимии) может выражать разный смысл.

Полное понимание языка требует знания смысла всех слов языка. Естественно потребовать, чтобы каждое имя имело точно один смысл. Такая однозначность обеспечивается в логике предикатов. А вот в обычных языках, как мы знаем, дело обстоит совсем не так.

2. Константы и переменные. Константа - это собственное имя. Примерами констант являются собственные имена чисел, людей, роботов.

Переменная - это символ, содержание которого совпадает с содержанием константы, за исключением лишь того, что единственный денотат константы заменен здесь возможностью различных значений переменной. С каждой переменной связана некоторая непустая область ее возможных значений. Поэтому к содержанию переменной относится в некотором смысле и содержание собственного имени области ее значений. Нужно особо подчеркнуть, что переменная в исчислении предикатов есть определенного рода символ, а не предмет (например, число), который этот символ обозначает.

3. Функции и термы. Функция - это операция, которая будучи применена к чему-то как к аргументу, дает некоторый объект в качестве значения функции для данного аргумента. В природе всякой функции лежит свойство быть применимой лишь к некоторым предметам.

Предметы, к которым функция применима, составляют область определения функции, а ее значения составляют область значении функции. Сама функция состоит в определении некоторого значения для каждого аргумента из области ее определения. Например, функция распознавания состоит в определении номера класса, к которому принадлежит объект, трактуемый как аргумент.

Для того чтобы обозначить значение функции для некоторого аргумента, обычно пишут имя этой функции и приписывают к нему справа имя аргумента, взятое в скобки. Так, если f - функция, а x принадлежит к области ее определения, то f(x) есть значение функции f для аргумента x. Если функция применима к упорядоченной системе из n аргументов, то она называется n-арной.

Важную роль в дальнейшем играют выражения для функций, значения которых принадлежат той же области, что и их аргументы. Такие выражения называются термами. Терм - это выражение, построенное, исходя из символов предметных переменных и констант, с помощью символов функций. Например, если f есть парная функция и уже известно, что х₁, ..., х_n - термы, то f(x₁, ..., х_n) есть терм. Содержательно терму соответствует имя некоторого предмета.

4. Предложения, высказывания и предикаты. Простейшим выражением в обычных языках является предложение. Предложение - это такое соединение слов, которое имеет самостоятельный смысл, т. е. выражает законченную мысль. Каждому предложению сопоставим высказывание (выражаемое этим предложением), предполагая при этом, что каждое высказывание или истинно, или ложно и не может быть одновременно и истинно, и ложно. Таким образом, высказывание можно рассматривать как величину, принимающую только два значения: "истина" (И) или "ложь" (Л).

Предположим теперь, что х представляет собой произвольный предмет из некоторого множества {х}, a F(x) - какое-либо высказывание о x. Выражение F(x) становится определенным, когда переменная x заменена определенным значением (именем предмета) из множества {x}. Например, выражение "x есть животное" становится вполне определенным высказыванием, если x - это робот (ложное высказывание) или если x - это собака (истинное высказывание).

Так как с нашей точки зрения каждое определенное высказывание представляет собой И или Л, то выражение F(x) означает, что каждому предмету из {х} поставлен в соответствие один из двух символов: И или Л. Иначе говоря, F(x) представляет собой функцию, определенную на множестве {х} и принимающую только два значения: И и Л. Аналогично неопределенное высказывание о двух, трех и более предметах представляет функцию со значениями И и Л от двух, трех и более переменных. Эти неопределенные высказывания (функции одной или нескольких переменных) вида F(x₁ ..., х_n) мы будем называть логическими функциями или предикатами.

5. Элементарные (атомарные) и правильно построенные формулы. Каков бы ни был символ n-местного предиката F и каков бы ни был выбор термов х₁ ..., х_n, (не обязательно различных), выражение F(x₁, ..., х_n) мы будем называть элементарной, или атомарной, формулой. Из этого определения следует, что, например, имена предметов не являются формулами.

Рассматривая элементарные формулы как величины, способные принимать только значения И и Л, мы определим над ними операции, которые позволяют из данных формул получать новые. Эти операции, по существу, выражают употребительные в обычных языках связки.

Если А и В - какие-либо данные формулы (т. е. либо элементарные формулы, либо уже построенные сложные формулы), то А∧В, A∨B, А→В, А↔В также являются (сложными) формулами. Если А - данная формула, то ¯|А - также (сложная) формула. Первые четыре операции - бинарные (двухместные), пятая - унарная (одноместная).

Символы ∧, ∨, →, ↔, ¯| называются соответственно конъюнкцией, дизъюнкцией, импликацией, эквивалентностью и отрицанием. Их можно читать, пользуясь словами, приведенными в правой части следующей таблицы:

∧ - "и";

∨ - "или", "... или, ... или", "и/или";

→ - "влечет", "если..., то...," "только если";

↔ - "равносильно", "эквивалентно", "тогда и только тогда",

¯| - "не", "неверно, что".

Прочтение сложных формул может стать неоднозначным, если не ввести скобок, указывающих, в каком порядке формулы связываются между собой. Поэтому мы будем писать (А → В) → С или А → (В → С), а не А → В → С. Впрочем, число скобок можно уменьшить, приписав нашим связкам убывающие "ранги" в следующем "порядке старшинства":

Там, где возможны были бы два способа построения формулы, связка более высокого ранга имеет большую область действия. Так, А → В∧С означает А → (В∧С). Связка ¯| имеет наименьший ранг, так что, например, ¯|А∨В означает (¯|А)∨В, а не ¯|(A∨B).

При построении сложных формул возникает вопрос, как определить значения сложных формул, зная значения простых формул, которые их составляют? Ответ на этот вопрос дается нижеследующей таблицей истинности.

Таким образом, A ↔ В истинно тогда и только тогда, когда A и В имеют одинаковые значения (почему ↔ и называют "эквивалентностью"); А → В ложно тогда и только тогда, когда А истинно, а В ложно; A∨В истинно тогда и только тогда, когда и А, и В истинны; А∨В ложно тогда и только тогда, когда и A, и В ложны; наконец, ¯|А истинно тогда и только тогда, когда A ложно.

Кроме пяти упомянутых символов-связок, в исчислении предикатов употребляются еще два символа, выражающие операции утверждения всеобщности и существования. Символ ∀x называется квантором всеобщности, а символ ∃x - квантором существования.

Формула ∀xF(x) истинна, когда F(x) истинно для каждого элемента х области {х}, и ложна в противном случае. Соответствующее ей словесное выражение будет: "для всякого хF(x) истинно". Формула ∃xF(x) истинна, если существует элемент области {х}, для которого F(x) истинно, и ложна в противном случае. В обычном языке этой формуле соответствует выражение: "существует х такое, что F(x) истинно".

Мы будем говорить, что в формулах ∀xF(x) и ∃xF(x) переменная х связана соответствующим квантором. Ясно, что сами эти формулы от х не зависят. Заметим, что ¯|(∀xF(x)) ↔ ∃x¯|F(x).

Теперь мы можем дать определение правильно построенной формулы (ППФ) на языке робота. ППФ называется выражение, которое может быть построено исходя из элементарных (атомарных) формул с помощью операций перехода от формулы A к формулам ∀хА и ∃хА, от формул A и B к формулам A∧B, A∨В, А → В, А ↔ В, ¯|А, ¯|В. Элементарная формула или ее отрицание, входящие в ППФ, называются литерами (или литералами), а дизъюнкция литер называется простым дизъюнктом.

6. Интерпретации. ППФ имеет смысл только тогда, когда имеется какая-нибудь интерпретация входящих в нее символов. Под интерпретацией мы будем понимать всякую систему, состоящую из непустого множества D, называемого предметной областью, и какого-либо соответствия, относящего каждому символу n-местного предиката некоторое n-арное отношение в D, каждому символу функции от n аргументов некоторую n-местную операцию в D и каждой константе - некоторый элемент из D. Например, если D есть множество всех роботов, то отношение между двумя роботами, состоящее в том, что первый из них совершеннее (по каким-то определенным параметрам) второго, можно отождествлять с множеством всех упорядоченных пар роботов (x, y) таких, что х совершеннее y. Таким образом, интерпретация осуществляет связь между языком робота и описываемой им предметной областью реального мира. Она позволяет придать ППФ содержательный смысл.

При заданной интерпретации всякая ППФ (не содержащая свободных переменных) представляет собой высказывание, которое истинно или ложно. Если при данной интерпретации каждая из ППФ A_i, i = 1, ..., n, имеет значение И, то будем говорить, что данная интерпретация удовлетворяет системе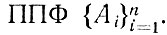  
ППФ A выводима (логически следует) из некоторой системы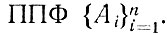  
если каждая интерпретация, удовлетворяющая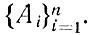  
удовлетворяет также и A. Так, очевидно, что ППФ ∀xF(x) выводима из системы ППФ {∀х¯|R(х)∨F(x), ∀xR(x)}.

Согласно теореме Гёделя, если некоторая интерпретация удовлетворяет заданной системе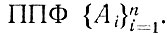  
то она удовлетворяет и любой ППФ A, выводимой из этой системы. Умение продемонстрировать, что ППФ А выводима (логически следует) из системы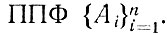  
когда это на самом деле так, играет важную роль при логическом анализе, и мы сосредоточим на нем свое внимание. Предположим, что А выводима из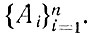  

Тогда любая интерпретация, удовлетворяющая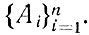  
удовлетворяет А, но не удовлетворяет ¯|А. Следовательно, никакая интерпретация не удовлетворяет объединению {A_i}_i=1ⁿ ∨ ¯|A. Если некоторая система ППФ не удовлетворяется ни при какой интерпретации, то она называется неудовлетворимой. Так, если ППФ А выводима из {A_i}_i=1ⁿ, то объединение {A_i}∨¯|A неудовлетворимо. И наоборот, если {A_i}_i=1ⁿ∨¯|A неудовлетворимо, то ППФ А должна логически следовать из системы ППФ {A_i}_i=1ⁿ. Именно эта концепция выводимости лежит в основе понятия логического вывода, или дедукции, в исчислении предикатов.

Универсальным методом логического вывода является так называемый метод резолюций [9], предложенный в 1965 г. Дж. Робинсоном. Этот метод замечателен тем, что он сложный процесс логического вывода сводит к последовательности очень простых операций, каждая из которых может быть легко запрограммирована.

В основе метода резолюций лежат три простых правила вывода (резольвенции):

1) если истинны ППФ А и ¯|A∨В, то истинна ППФ B (правило modus ponens);

2) если истинна ППФ A∨А, то истинна ППФ А (правило факторизации);

3) если истинна ППФ А(х), то истинна ППФ ∀yА(y).

Эти правила применяются к простым дизъюнктам, на которые предварительно "раскладывается" система ППФ {A_i}_i=1ⁿ∨¯|A, из неудовлетворимости которой следует, что А выводима из {A_i}_i=1ⁿ. Новые дизъюнкты, получаемые в результате применения указанных правил, называются резольвентами. При образовании резольвент существенную роль играет процедура унификации, которая для двух данных предикатов осуществляет подстановку термов вместо переменных, делающую предикаты одинаковыми. После этого к полученным ППФ применяются правила резольвенции. Например, для неудовлетворимой системы ППФ вида {A(x)∨B(x), ¯|B(f(z)), ¯|A(f(z))}, используя первое правило вывода после подстановки терма f(z) вместо переменной x, получим из первых двух ППФ резольвенту А(f(z)), которая в сочетании с третьей ППФ системы дает нулевую формулу.

Таким образом, если выбрано два простых дизъюнкта и по одной литере в каждом из них, то применение правила унификации и затем правил вывода дает резольвенту. При доказательстве выводимости ППФ А, рассматриваемой как заключение (теорема), из заданной системы ППФ {A_i}_i=1ⁿ, рассматриваемых как посылки (аксиомы), процесс образования резольвент (в котором могут принимать участие и ранее полученные резольвенты) продолжается, пока не будет получена пустая формула, означающая неудовлетворимость системы {A_i}_i=1ⁿ∨¯|A и успех доказательства. Важно отметить, что число резольвент, формируемых при доказательстве любой теоремы из заданной конечной системы аксиом, конечно.

В ряде задач, которые должны решать интеллектуальные роботы, простое доказательство выводимости ППФ A, формулирующей задание, из системы ППФ {A_i}_i=1ⁿ, описывающих условия выполнения этого задания, оказывается недостаточным. Примером такой задачи является задача планирования поведения робота. В подобного рода задачах нужно знать то значение переменной х, при котором данная ППФ А(х) логически выводима из некоторой системы ППФ {A_i}_i=1ⁿ. Иными словами, мы (вместе с роботом) хотели бы знать, следует ли логически ППФ ∃хА(х), и если да, то каково то значение х, при котором существует решение. Заметим, что умение отыскивать такие значения для переменной, связанной квантором существования, позволяет ставить роботу вопросы весьма общего характера и осуществлять диалог с ним. Например, мы могли бы спросить у робота: "Какие действия и в какой последовательности нужно совершать, чтобы собрать из деталей определенную конструкцию?". Ответом на этот вопрос будет не просто констатация факта, что сборка данной конструкции возможна, а развернутый план (технологический маршрут) сборки.

Рассмотрим на простейшем примере, как могут решаться подобного рода задачи. Пусть роботу известно, что его манипулятор жестко закреплен на подвижной платформе, а платформа находится в цехе. Спрашивается: "где находится манипулятор?". В этой задаче сформулированы два "факта", которые можно записать в виде двух правильно построенных формул:

где двухместному предикату Р(у, z) придана очевидная интерпретация: "у находится в z". На вопрос "где находится манипулятор?" робот может дать ответ, если сначала докажет, что правильно построенная формула

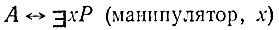
выводима из системы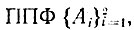  
и затем найдет то значение х (константу), которое на самом деле "существует" и служит ответом.

Используя описанный выше метод резолюции, робот сначала попытается доказать неудовлетворимость системы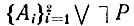  
(манипулятор, х). (Заметим, что отрицание ППФ А есть ППФ ¯|P (манипулятор, x)). Процесс доказательства неудовлетворимости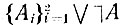  
представлен на дереве вывода, изображенном на рис. 10.

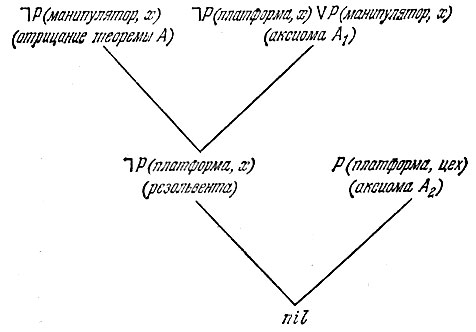
Рис. 10. Дерево вывода

Из этого дерева вывода можно извлечь также ответ на наш вопрос: "где находится манипулятор?". Это осуществляется следующим образом. Сначала к отрицанию теоремы добавляется ее отрицание, т. е. сама теорема. В результате получается тавтология (т. е. ППФ, тождественно истинная при всех интерпретациях) вида ¯|Р (манипулятор, х) ∨ Р (манипулятор, х). Затем в соответствии со структурой дерева вывода, изображенного на рис. 10, вновь формируются резольвенты до тех пор, пока в корне дерева не получится некоторая ППФ, играющая роль ответа на языке робота. В нашем примере получим одну резольвенту ¯|Р (платформа, х) ∨ Р (манипулятор, х), а в корне дерева - ППФ Р (манипулятор, цех), в которой содержится ответ на вопрос "где находится манипулятор?". Заметим, что форма ответа на языке робота близка к форме теоремы-вопроса. В нашем случае единственное отличие состоит в том, что в теореме-вопросе содержится переменная, связанная квантором существования, а в ответной ППФ - константа (ответный терм).

Таким образом, описанная система логического вывода, основанная на методе резолюций, представляет собой эффективное средство для автоматического поиска доказательств (отыскания логических следствий) и извлечения ответа в терминах исчисления предикатов. Мы рассмотрели основные понятия этого исчисления и связанного с ним метода резолюций не ради них самих, а чтобы понять и продемонстрировать, как робот, используя этот язык, может логически рассуждать, обучаться новому и адаптироваться в процессе решения интеллектуальных задач.