Системы управления, использующие силовую информацию

Применение вышеописанных двухсторонних сервомеханизмов оказало чрезвычайно благотворное влияние на развитие дистанционно управляемых копирующих манипуляторов, привело к расширению их функциональных возможностей и появлению новых областей внедрения этих манипуляторов. Более того, если бы силовая обратная связь не передавалась от ведомого манипулятора к ведущему, эффективное управление копирующими системами оказалось бы просто невозможным. В этом случае любой самый квалифицированный оператор в течение нескольких минут совершенно выбился бы из сил, устав от безрезультатных неконтролируемых попыток совладать с рабочим объектом с помощью расположенного на удалении ведомого манипулятора. В самом деле, выполнение любых физических манипуляций, за результатами которых можно следить лишь через узкое застекленное окошко в перегородке или на экране телевизора, в отсутствие возможности ощущать ответную реакцию объекта не приведет ни к чему, кроме раздражения и крайнего нервного напряжения оператора.

Все сказанное в равной степени относится и к случаю управления манипулятором промышленного робота от компьютера. Другими словами, даже если захватное устройство робота оборудовано датчиками касания и давления, без информации об усилиях вряд ли с помощью одного лишь компьютера удастся организовать достаточно эффективное управление работой манипулятора робота.

К настоящему времени предложены три подхода к учету силовой информации при управлении манипулятором, т. е. три способа управления с силовым очувствлением. Первый из них заключается в добавлении к обычным сервосистемам управления позицией звена каких-либо датчиков для измерения усилий, приложенных к данному звену. Второй способ, напротив, предусматривает создание систем силового управления приводами и установление каким-либо образом связи между усилием, приложенным к приводу, и текущим положением управляемого звена. В зависимости от исходного управляющего устройства одни системы называют системами управления с позиционным доминированием, а другие - системами управления с силовым доминированием. Системы третьего типа появились совсем недавно; они могут произвольно переключаться с управления с позиционным доминированием на управление с силовым доминированием.

Робот с силовым очувствлением (пример № 1)

Как следует из вышесказанного, существуют три основные разновидности систем управления с позиционным доминированием, или, другими словами, двухсторонние сервосистемы, - симметричные, с обратной передачей усилия, силовые возвратные. Наиболее успешной попыткой применения двухсторонних сервосистем для силового управления манипуляторами оказалась работа профессора Токийского университета Иноуэ. Иноуэ в обычной схеме копирующей двухсторонней симметричной системы (рис. 3.47, б) заменил ведущий привод компьютером и в результате получил замкнутую систему управления (рис. 3.49). В этой системе целевое значение угла поворота управляемого звена преобразуется с помощью цифро-аналогового преобразователя (ЦАП) в электрическое напряжение. Последнее сравнивается с напряжением, соответствующим текущему значению угла поворота. Разность напряжений, которая является аналоговым представлением рассогласования, после аналого-цифрового преобразования поступает в компьютер. Компьютер по величине рассогласования вычисляет коррекцию усилия, направленного против приложенных к управляющему звену внешних сил. Таким образом реализуется управление с силовым очувствлением.

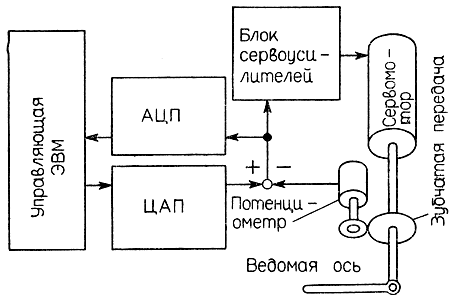
Рис. 3.49. Пример использования симметричной двухсторонней сервосистемы

Рассмотрим некоторые детали изложенного метода управления. Обычная двухмерная позиционная аналоговая сервосистема определяется уравнением

где r - целевое назначение позиции; θ - изменение выходного угла поворота управляемой оси; J - момент инерции; К_b - коэффициент вязкого сопротивления; K_a - жесткость всей системы; τ_l - момент нагрузки.

Обозначим также через е значение рассогласования между целевым и текущим значениями углов поворота, т. е. е = r - θ, и выполним преобразование Лапласа над уравнением (3.100). Положим все начальные значения в (3.100) равными нулю. В результате получим следующее выражение для преобразования Лапласа от рассогласования е:

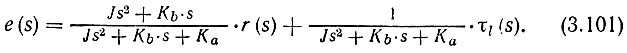
После того как реакция системы управления на заданное целевое значение позиции и внешний момент нагрузки примут установившееся значение, величина рассогласования е будет описываться равенством е = τ_l / K_а, т. е. при таком управлении рассогласование по позиции практически пропорционально моменту внешней нагрузки.

Благодаря полному использованию силовой информации, поступающей от приводов каждой степени подвижности, и силовому и тактильному очувствлению захватного устройства профессору Иноуэ удалось создать манипулятор, который, получив от оператора лишь самую простую инициирующую команду, способен автоматически вставлять стерженьки в отверстия, крутить рукоятки и выполнять множество других, непосильных для обычных роботов, операций. Например, операции типа вал - втулка (в данном случае в роли вала выступает гладкий металлический цилиндр) выполняются этим роботом в следующей последовательности (рис. 3.50):

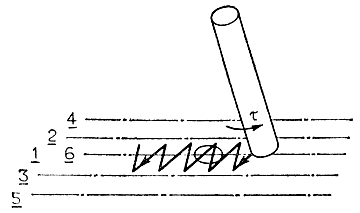
Рис. 3.50. Последовательность выполнения операции вставления вала во втулку

1 цилиндр зажимается губками захватного устройства и слегка наклоняется для облегчения попадания в отверстие;

2 захват с цилиндром медленно опускается по направлению к пластине, в которой сделано отверстие, при этом с помощью расположенных в запястье силовых датчиков проверяется, попал ли цилиндр в отверстие или нет;

3 если зафиксировано касание цилиндра поверхности пластины, т. е. цилиндр не попал в отверстие, попытка вставления приостанавливается;

4 в этом случае захват начинает совершать поисковые движения таким образом, что кончик цилиндра, касаясь поверхности пластины, описывает пилообразную траекторию (рис. 3.50). На протяжении всего поиска с помощью силовых датчиков контролируется величина крутящего момента τ; если эта величина резко изменилась, предполагается, что отверстие обнаружено, и цилиндр с небольшим усилием направляется в отверстие;

5 после того как кончик цилиндра вошел в отверстие, захватное устройство, поддерживая неизменной позицию кончика, исправляет ориентацию цилиндра до тех пор, пока он не займет строго вертикального положения прямо над отверстием (рис. 3.51). Естественно, что в процессе выравнивания никак не обойтись без использования силового очувствления захвата и шарниров манипулятора;

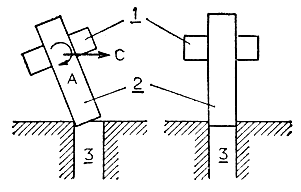
Рис. 3.51. Коррекция ориентации руки робота при вставлении вала во втулку. 1 - искусственная рука (захват); 2 - вал; 3 - втулка

6 при легких покачиваниях вперед-назад и вправо-влево цилиндр вводится в отверстие на заданную глубину, и здесь опять-таки используется информация о распределении сил и моментов.

В качестве еще одного примера расширения функциональных возможностей роботов в результате силового очувствления рассмотрим выполнение роботом профессора Иноуэ операции вращения рукоятки. Умение вращать рукоятку может пригодиться роботу, в частности, при открывании и закрывании двери. В самом деле, как показано на рис. 3.52, траектории, которые описывает захватное устройство при открывании двери за ручку и при вращении рукоятки, и в том и в другом случае представляют собой дугу окружности. Вообще говоря, вращение рукоятки относится к более широкому классу операций, в которых свобода перемещения манипулятора от начала до целевой точки подвергается дополнительным внешним ограничениям, возникающим с момента захвата объекта манипулирования. Очень часто с такими операциями приходится сталкиваться и человеку, и животным. Роботизация операций, накладывающих дополнительные кинематические ограничения, при помощи одного лишь позиционного управления представляет собой чрезвычайно трудную, если вообще разрешимую, проблему. Впрочем, если удалось бы реализовать чисто позиционное управление операциями вращения, то это, наверняка, было бы очень специфичным решением, ориентированным на конкретные условия частной задачи. О гибкости выполнения операций вращения при чисто позиционном управлении не может быть и речи.

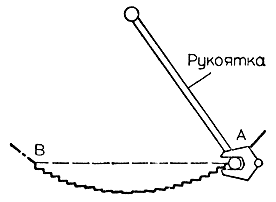
Рис 3.52. Выполнение роботом операции вращения рукоятки

Основу предложенного Иноуэ метода управления операциями вращения при силовом очувствлении робота составляет алгоритм определения текущей позиции захватного устройства под воздействием реакции со стороны объекта манипулирования. Блок-схема этого алгоритма показана на рис. 3.53 (собственно к определению позиции имеет отношение только левая ветвь условного блока С). Способ определения позиции заключается в измерении величины позиционного рассогласования, которое возникает и изменяется в результате принудительного перемещения звеньев манипулятора, управляемых обычными позиционными сервосистемами. Величина и направление принудительного перемещения обусловлены равнодействующей двух сил, приложенных к оси подвижности манипулятора, - силы электропривода, стремящейся повернуть звено на изначально заданную величину, и силы реакции рукоятки, возникающей из-за наличия ограничений возможности ее перемещения. Измеренное значение рассогласования между целевой позицией и текущей, зависящее от значения равнодействующей сил привода и реакции, используется для вычисления коррекции изначального целевого значения. Следовательно, при данном способе управления целевое значение не поступает извне, как в обычных позиционных сервосистемах, а определяется в процессе управления с учетом кинематических особенностей объекта манипулирования. Новое целевое значение, определенное исходя из текущего распределения сил, передается в компьютер для расчета корректирующих воздействий на приводы. Поступая в компьютер, каждое новое целевое значение заменяет предыдущее, в том числе и изначальное целевое воздействие, вычисленное исходя лишь из позиции, которую должен занимать объект манипулирования в конце операции, без учета ограничений на степени подвижности этого объекта.

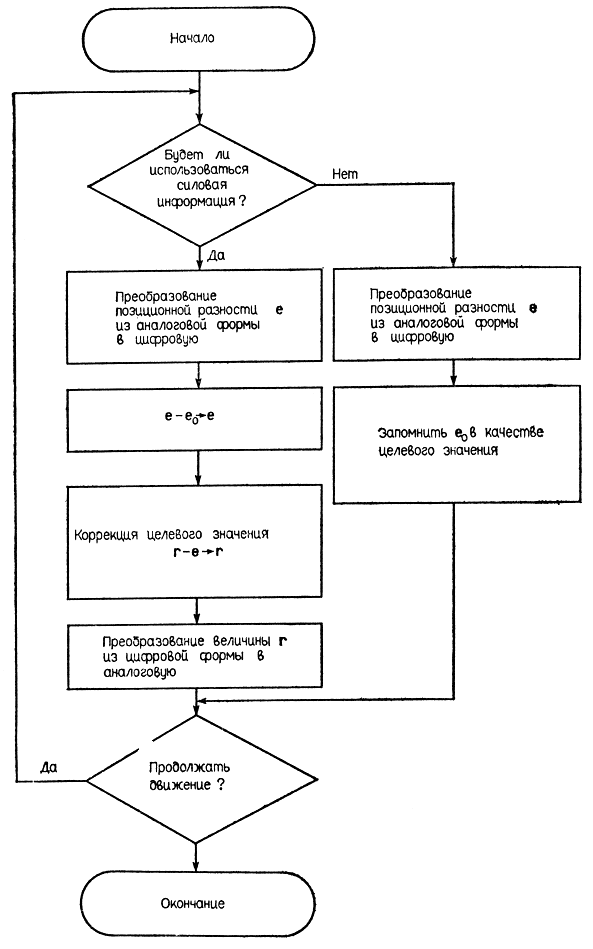
Рис. 3.53. Алгоритм определения локальной целевой позиции захвата за счет анализа сил реакции со стороны перемещаемого объекта

В общем случае для выполнения операций вращения роботу с силовым очувствлением достаточно получить только инициирующую команду с указанием начального и конечного положений объекта манипуляции. Например, в ситуации, показанной на рис. 3.52, роботу, захват которого удерживает рукоятку в точке А, необходимо указать только целевую точку В. При выполнении команды вращения робот будет стремиться переместить захват в изначально заданное целевое положение В по кратчайшей траектории. Однако в процессе перемещения изначальное целевое значение будет замещаться последовательностью локальных текущих целевых значений. Локальное целевое значение вычисляется в соответствии с вышеизложенным алгоритмом с учетом силы реакции перемещаемого объекта, обусловленной наличием ограничений на число степеней подвижности этого объекта (рукоятки). Измерения силы реакции осуществляются с помощью силомоментных датчиков, расположенных в каждом шарнире и в захватном устройстве. Как показано на рис. 3.52, траектория, реализованная в результате многократной коррекции изначального целевого значения, состоит из очень большого числа квазилинейных участков, каждый из которых соответствует перемещению захвата под действием текущего целевого воздействия за время вычисления очередной коррекции этого воздействия.

Робот с силовым очувствлением (пример № 2)

Принципы силового очувствления антропоморфного манипулятора MELARM-I чрезвычайно просты. Как показано на рис. 3.54, упругий стержень, помещенный между ведомым и ведущим звеньями, служит не только для передачи усилия от ведущего привода, но и для измерения величины внешней силы, приложенной к ведомому звену. Эта величина оказывается пропорциональной величине деформации стержня, которая измеряется тензометром. Несмотря на то что такой способ измерения сил и моментов сам по себе прост, реализация его на практике для многозвенных манипуляторов со сложными кинематическими схемами является далеко не тривиальной задачей, причем наибольшую трудность вызывает оптимальное расположение силомоментных датчиков в шарнирах манипулятора.

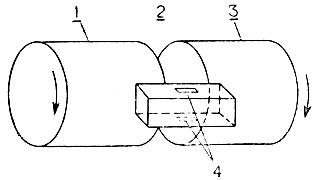
Рис. 3.54. Принцип работы силомоментного датчика. 1 - ведущее звено; 2 - упругий стержень; 3 - ведомое звено; 4 - тензокетр

Что касается робота MELARM-I, то силомоментными датчиками оснащены шарниры каждой из семи степеней подвижности (рис. 3.55). Принятая для этого робота методика измерения сил мало чем отличается от методов обнаружения соприкосновения. Как тот, так и другой основаны на описанном выше принципе минимизации рассогласования в сервосистемах. Однако при измерении внешних усилий не следует забывать, что показания силомоментных датчиков в шарнирах в той или иной степени зависят от текущей конфигурации звеньев манипулятора. Эта зависимость становится особенно заметной для мощных манипуляторов с большим собственным весом, подобных MELARM-I. Поэтому, чтобы в каждый момент времени знать истинное значение приложенного к захвату внешнего усилия, необходимо рассчитывать с помощью ЭВМ составляющую, которая определяется собственным весом и конфигурацией манипулятора, и вычитать ее из текущих показаний силомоментных датчиков. От того, насколько точно удается реализовать на практике компенсацию моментов сил тяжести звеньев, в конечном итоге зависит общая эффективность алгоритмов управления с силовой обратной связью.

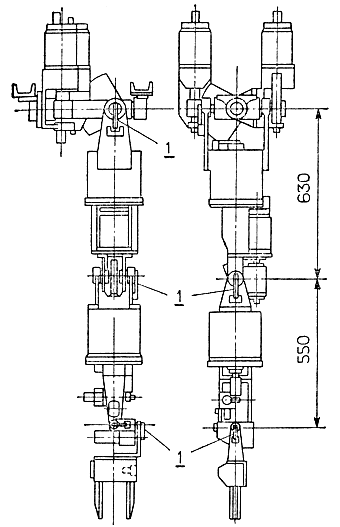
Рис. 3.55. Расположение силомоментных датчиков в шарнирах робота. 1 - силомоментный датчик

В данном случае определение влияния веса звеньев осуществляется следующим образом (рис. 3.56). Запишем уравнения для момента T₁, приложенного к шарниру θ₁, в виде

где z_α = λ₁z₁ + (1 - λ₂) z₂, z_β = λ₂z₂ + (1 - λ₃) z₃, z_γ = α₃z₃, z₁ = (0, 0, m₁g)^Т, z₂ = (0, 0, -m₂g)^T, z₃ = (0, 0, -m₃g)^Т. Здесь S - плечевой сустав, Е - локтевой сустав, W - запястье, Н - позиция некоторой точки, связанной с захватом (позиция захвата); l₁ = SE, l₂ = EW, l₃ = WH; z₁, z₂, z₃ - векторы силы тяжести соответственно для плечевого и локтевого звеньев и захватного устройства; λ₁, λ₂, λ₃ - расстояния от начала соответствующего звена до центра тяжести этого звена; i, j, k - базисные единичные векторы неподвижной системы координат; а Р_Е, Р_W, Р_Н - векторы позиций локтевого сустава, запястья и захвата; m₁, m₂, m₃ - массы плечевого и локтевого звеньев и захвата.

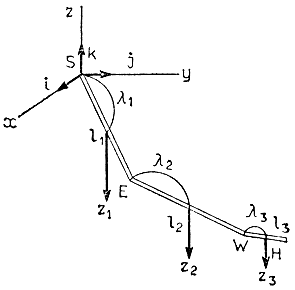
Рис. 3.56. К расчету влияния собственного веса звеньев манипулятора на показания силомоментных датчиков

Аналогично для моментов, приложенных к шарнирам θ₁, θ₂, θ₃, имеем

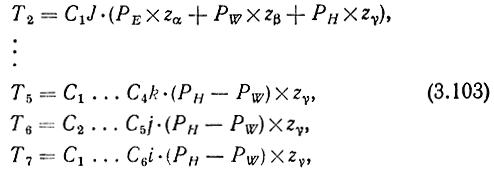
где C₁, ..., C₇ - матрицы преобразования координат.

♦♦♦ Заметим, что уравнения (3.102), (3.103) справедливы лишь для идеализированной модели манипулятора, в которой все звенья представлены прямолинейными стерженьками и соединены идеальными шарнирами. Следовательно, они являются лишь так называемым первым приближением реальной ситуации.

В практических случаях при вычислении величины компенсации приходится учитывать погрешности позиционирования вала электропривода и несбалансированность конструкции реального манипулятора. В результате уравнения для расчета моментов в шарнирах приобретают более сложный вид, нежели их идеализированные аналоги (3.102), (3.103). Тем не менее и для реального манипулятора удается так составить уравнения компенсации, что расчетная величина погрешности, обусловленной особенностями конструкции реального робота, очень хорошо согласуется с действительными значениями отклонения от идеализированной модели. Таким образом, в результате вычисления компенсации сил тяжести звеньев с учетом конструкционных погрешностей манипулятора можно практически исключить влияние собственной массы звеньев на точность измерения внешних сил и моментов.

Допустим теперь, что к захвату, как показано на рис. 3.57, приложена внешняя сила z_f. Возникающее при этом в каждом шарнире возрастание результирующего момента можно вычислить по формулам

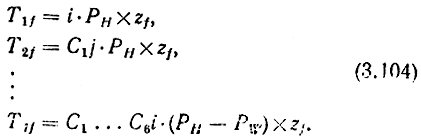
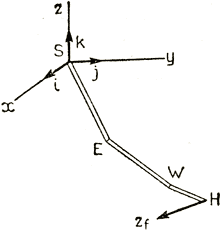
Рис. 3.57. Внешнее усилие, приложенное к захвату

Эти уравнения используются для управления манипулятором с силовым очувствлением в реальном масштабе времени. С помощью силовой обратной связи робот MELARM-I способен выполнять различные нетривиальные операции, недоступные его неочувствленным аналогам. В частности, силовая обратная связь может применяться для координации взаимодействия двух рук в процессе выполнения одной операции. Например, робот MELARM-I, как показано на рис. 3.58, с помощью двух манипуляторов легко справляется с захватом и переносом в заданное место большой тяжелой коробки. В то же время реализация согласованного взаимодействия двух многозвенных манипуляторов при простом позиционном управлении оказалась настолько сложной задачей, что от практического применения взаимодействия неочувствленных роботов пришлось отказаться.

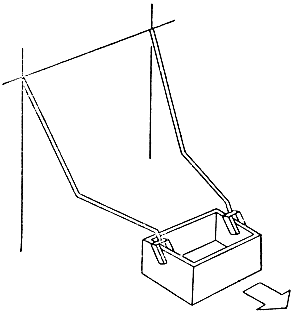
Рис. 3.58. Согласованное взаимодействие двух рук манипулятора при перемещении крупногабаритного объекта

При организации взаимодействия двух роботов с силовым очувствлением один из них является ведущим и может управляться чисто позиционно, а другой - ведомым и с помощью силовой обратной связи подстраивается под траекторию, по которой движется первый робот. В частности, в примере, показанном на рис. 3.59, роль ведущего отводится роботу, расположенному справа. Захват этого робота перемещается прямо в заданную точку с помощью чисто позиционного управления. В это время левый робот, анализируя распределение моментов и сил в шарнирах, которые вызваны внешней силой со стороны ящика, перемещаемого правым роботом, непрерывно корректирует заданную траекторию движения захвата. В результате захват левого робота перемещается по траектории, диктуемой правым, ведущим роботом.

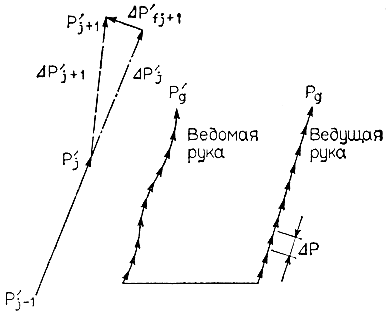
Рис. 3.59. Метод коррекции позиции захвата ведомого манипулятора в процессе согласованного взаимодействия двух рук манипулятора при перемещении одного объекта

В этом примере вектор Р_Н позиции захвата ведомого робота в системе координат ведущего робота трансформируется в вектор Р'_H в соответствии со следующим выражением:

где l₀ - расстояние между запястьями двух роботов (рис. 3.60). Именно вектор Р'_Н удовлетворяет системе уравнений (3.105). Таким образом, если предположить, что левый борт ящика образует одно целое с захватом левого робота, то G помощью выражений (3.104), (3.108) можно непосредственно вычислить величину внешнего усилия, которое правый робот прикладывает к правому борту ящика. При этом поправка для компенсации неустранимой погрешности позиционирования захвата левого робота рассчитывается по следующим формулам:

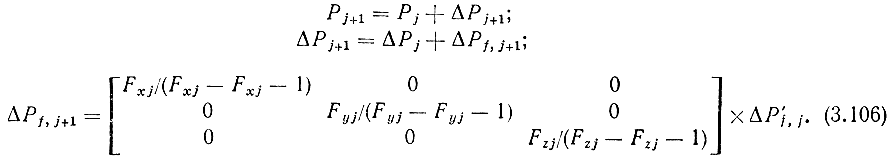
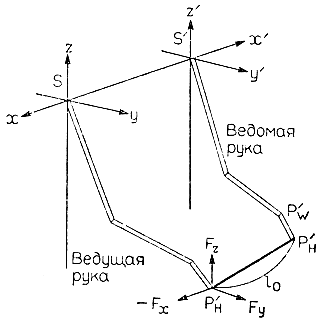
Рис. 3.60. Метод вычисления позиции захвата в процессе согласованного взаимодействия двух рук манипулятора

Робот с силовым очувствлением запястья

Помимо роботов с силовым очувствлением всех шарниров большое практическое распространение получают роботы с силомоментными датчиками, расположенными только в запястье. Основным преимуществом очувствления запястья по сравнению с полным очувствлением является простота расчета внешнего усилия, а следовательно, и легкость организации управления с силовой обратной связью в реальном масштабе времени. Однако если робот с очувствленным запястьем предполагается использовать для работы с большими нагрузками, то в этом случае необходимы силомоментные датчики, удовлетворяющие двум противоречивым требованиям - они должны обладать большой жесткостью и сохранять при этом высокую чувствительность.

На рис. 3.61 представлена разработанная фирмой Hitachi по проекту Гото робототехническая система для выполнения прецизионных операций вставления. В этой системе каждый из роботов обладает гибким запястьем, в котором с четырех сторон установлены тензометры. Благодаря силовому очувствлению эти роботы с очень высокой скоростью могут выполнять операции вставления валов диаметром до 20 мм при зазоре в отверстии всего 7-32 мкм.

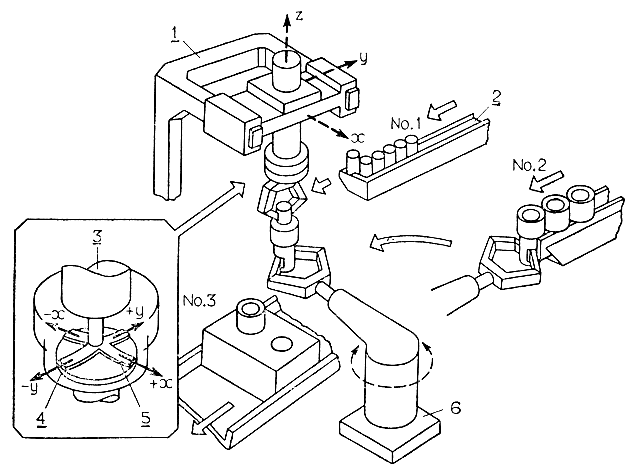
Рис. 3.61. Робот для выполнения прецизионных операций вставления. 1 - основной робот; 2 - устройство подачи заготовки; 3 - гибкое запястье; 4 - цилиндрический диск; 5 - пружинный тензометрический датчик; 6 - вспомогательный робот

На рис. 3.62 показан робот, разработанный в исследовательском центре Dripers laboratory (США) под руководством С. Невинса. Запястье этого робота также обладает силовым очувствлением, причем цилиндрические стержни с силомоментными датчиками крепятся к корпусу запястья с помощью мягких втулок, образуя таким образом подвижные скользящие пары (рис. 3.62). Следовательно, помимо силового очувствления это запястье имеет некоторую пассивную податливость. В результате манипулятор Невинса может применяться для установки шарикоподшипников на вал при зазоре 13 мкм.

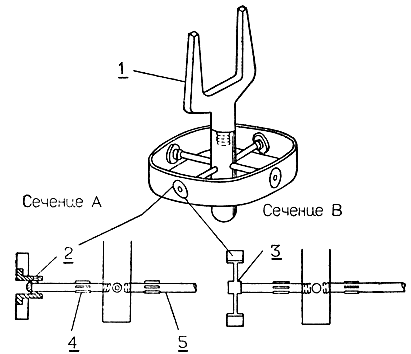
Рис. 3.62. Специализированное захватное устройство для выполнения операций вставления. 1 - основной манипулятор; 2 - шарик; 3 - мембрана; 4 - кремниевый тензометр; 5 - закрепленный с одной стороны цилиндрический упругий стержень