Манипуляторы с силовым управлением [1988 Накано Э.

Рассмотрим некоторые принципы построения систем управления, в которых в качестве управляемой величины используется главным образом выходное усилие, развиваемое захватом, а не его конфигурация. Для этого воспользуемся примером конкретных роботов, а именно манипулятором с непосредственным управлением моментами сил в шарнирах^*, гидравлическим "адаптивным роботом" д-ра Идо^** и роботом CMU Arm^***.

^* (Разработан в Электротехническом исследовательском центре (Токио) под руководством д-ра Такасэ на основе применения электромагнитных порошковых муфт.)

^** (Научно-исследовательский центр проблем механики (Токио).)

^*** (Построен в Университете Карнеги-Меллона (США) под руководством д-ра Асада.)

Многозвенный манипулятор с силомоментным управлением

Устройство и принципы работы сервосистемы

В 1973 г. под руководством д-ра Такасэ был разработан манипулятор с непосредственным управлением моментом вращения электроприводов каждой из семи степеней подвижности. Главное достоинство этого манипулятора - прямое управление от компьютера моментом сил, приложенных к каждому из шарниров, - обусловлено применением специальных электромагнитных порошковых муфт. Эти муфты предназначены для передачи усилия от электропривода к шарниру. Они обладают линейной рабочей характеристикой, т. е. величина выходного момента сил, приложенных к управляемой оси, пропорциональна силе тока на входе и не зависит от числа оборотов вала электропривода.

Устройство электромагнитной порошковой муфты показано на рис. 3.63. Поясним с помощью этого рисунка принципы работы муфты. Если в обмотку возбуждения подать ток намагничивания, то частички порошка из материала с высокой магнитной проницаемостью будут притягиваться в направлении радиуса обмотки и, следовательно, будет возрастать сила трения между цилиндрической поверхностью ведомого вала и порошком муфты. Увеличивая напряжение в обмотке возбуждения, мы пропорционально увеличиваем силу притяжения порошка и можем таким образом управлять величиной момента сил, приложенных к ведомой оси. Очевидно, если электромагнитную порошковую муфту жестко прикрепить к ведущей втулке, то ее можно использовать в качестве тормоза с управляемой переменной величиной силы торможения.

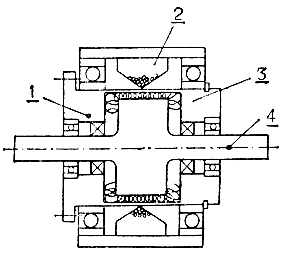
Рис. 3.63. Электромагнитная порошковая муфта. 1 - ведущая втулка; 2 - порошок; 3 - обмотка возбуждения; 4 - ведомый вал

На рис. 3.64 представлена структурная схема привода с электромагнитными порошковыми муфтами. Для каждой степени подвижности применяются две пары установленных друг против друга муфт и тормозов. Так как главной целью, преследуемой при разработке данного манипулятора, было обеспечение непосредственной управляемости моментами сил в шарнирах, для упрощения управляющих алгоритмов потребовалось всеми средствами добиваться максимально возможного уменьшения массы подвижной части манипулятора. Поэтому было принято решение отказаться от размещения приводов непосредственно на ведущих звеньях манипулятора и сосредоточить все приводы в одном месте на неподвижном основании. При этом, как показано на рис. 3.65, управляющие моменты сил передаются к каждой из степеней подвижности с помощью системы тросов. Такое решение привело не только к уменьшению массы подвижной части, но и к значительному упрощению всей конструкции манипулятора.

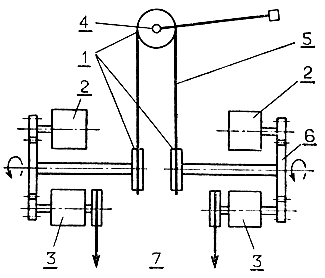
Рис. 3.64. Устройство привода с электромагнитными порошковыми муфтами. 1 - вращающийся блок; 2 - тормоз; 3 - муфта; 4 - ось вращения; 5 - трос; 6 - зубчатая передача; 7 - передача от электромотора

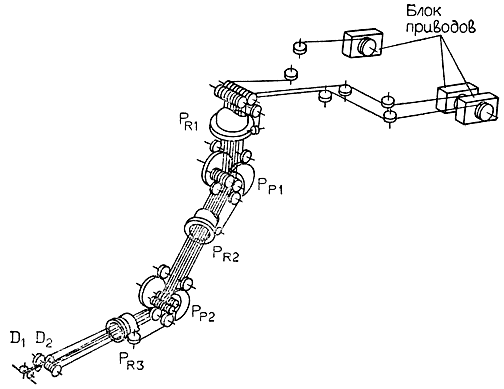
Рис. 3.65. Манипулятор с непосредственным управлением моментами сил в шарнирах (схема размещения приводных тросов)

Устройство сервосистемы этого манипулятора показано на рис. 3.66, а. Требуемая величина момента сил в каждом из шарниров рассчитывается компьютером по заданному алгоритму с учетом сигналов обратной связи нескольких видов. Таким образом, данную сервосистему можно рассматривать как систему автоматического управления, в контуре которой находится блок программного обеспечения компьютера (3.66, б).

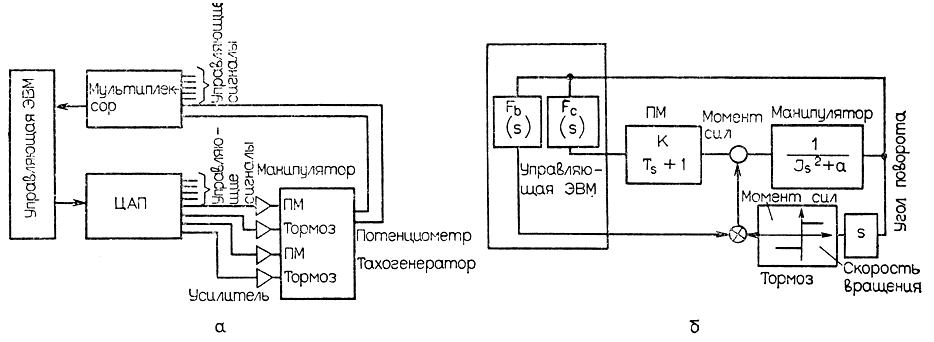
Рис. 3.66. Устройство сервосистемы манипулятора с непосредственным управлением моментами сил в шарнирах. F_c(s) и F_b(s) - передаточные функции муфты и тормоза соответственно

Метод управления

Рассмотрим манипулятор с шестью степенями подвижности. Допустим, что величина статического усилия, действующего на захват в точке P_h, равна F₁. Тогда соответствующие моменты сил в каждом из шарниров вычисляются по формулам T_fi = (r_i × F) · a_i (i = 1, ..., 6), где r_i - расстояние от шарнира i до точки P_h, a_i - единичный вектор, показывающий направления вращения звена в шарнире i (рис. 3.67). Если к моментам, вызванным внешним усилием, добавить расчетные значения моментов T_gi, компенсирующих в каждый момент времени собственный вес манипулятора, то результирующее значение моментов сил, приходящееся на каждый из шарниров, окажется равным сумме T_fi + T_gi. Управляя величиной этой суммы в каждом из шарниров, можно управлять величиной усилия F, развиваемого захватом в точке P_h.

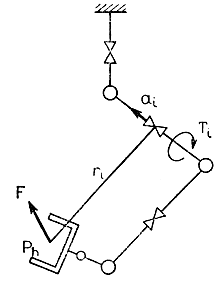
Рис. 3.67. Схема к анализу распределения сил в шарнирах манипулятора

Допустим теперь, что в трехмерном пространстве задана произвольная плоскость. Рассмотрим методы силового управления движением захвата робота, при условии что захват должен постоянно касаться этой плоскости.

Плоскость, в которой должен двигаться захват, определим с помощью одной точки Р_а, принадлежащей этой плоскости, и нормального вектора N_a. Величина силы связи F_a между плоскостью и захватом пропорциональна расстоянию от точки P_h до плоскости и определяется формулой F_a = - К (Р_h - P_a) · N_a. Подбирая моменты сил в каждом из шарниров так, чтобы обеспечить в точке P_h требуемое значение силы связи, можно управлять связанным движением захвата по произвольной плоскости. В данном примере плоскость в пространстве накладывает одно ограничение на характер движения захвата. Если потребовать, чтобы движение захвата удовлетворяло двум уравнениям связи, то траектория его движения будет представлять собой линию пересечения двух задающих плоскостей, а если задающих плоскостей будет три, то условиям связи будет удовлетворять лишь единственная точка пространства.

Практическими примерами операций, в которых рука робота должна перемещаться вдоль заданной плоскости, оказывая на эту плоскость постоянное давление f_р, могут служить шлифование с помощью наждачной бумаги или протирание классной доски. Если обозначить через N₀ нормальный фактор рабочей плоскости, то усилие, которое должен развить захват, в обоих случаях будет определяться формулой F = - f_p N₀. Аналогичным образом можно найти условия связи при двух ограничениях. Пусть, например, требуется провести прямую линию по линейке. Обозначив через N₁ и N₂ соответственно нормальные вектора плоскости бумаги и боковой грани линейки, сразу получаем необходимые условия в виде следующей пары уравнений: F₁ = - f₁N₁, F₂ = - f₂N₂.

Еще одним очень распространенным на практике случаем применения силового управления является управление перемещением объекта, на характер движения которого наложены ограничения в виде различных кинематических связей. Ярким примером может служить, в частности, операция вращения рукоятки. Чтобы повернуть рукоятку, необходимо приложить постоянное усилие, направленное по касательной к окружности, которую описывает рукоятка в процессе движения. Если обозначить через f_t величину касательной силы, через R единичный вектор, задающий направление поворота, и через Р_с центр вращения рукоятки, то величина усилия F_t, которое должен развивать захват манипулятора при выполнении операции вращения, будет определяться следующим уравнением:

В процессе управления вращением касательная сила F_t пересчитывается в каждый момент времени в зависимости от изменения координат точки P_h. В свою очередь эти координаты вычисляются по значениям углов в шарнирах манипуляторов, которые непосредственно считываются из показаний угловых потенциометров. Вычисленное значение силы F_t распределяется соответствующим образом по всем шарнирам манипулятора, к моментам внешней силы F_t добавляются текущие значения моментов, компенсирующих собственный вес манипулятора. Полученные суммы являются задающими значениями для сервосистемы каждого из приводов. В результате обеспечивается плавное вращение рукоятки с заданной скоростью.

Лабораторные испытания рассмотренного выше манипулятора с силовым управлением вызывают огромный интерес. Однако его практическое применение, по-видимому, может быть довольно ограниченным. Объясняется это двумя причинами, Во-первых, чтобы избежать растяжения и провисания тросов, приходится ограничиться лишь небольшими легкими объектами манипулирования. Это означает, что манипулятор такой конструкции не может использоваться в производственных условиях для работы с тяжелыми деталями. Во-вторых, данный робот не имеет силового очувствления, поэтому применение его для выполнения прецизионных операций превращается в трудноразрешимую задачу.

Силовое управление манипулятором с гидравлическими приводами

Этот манипулятор был разработан под руководством известного ученого д-ра Идо^* и называется "Адаптивный робот". Система управления манипулятора представляет собой комбинацию сервосистемы гидравлических приводов с системой автоматической балансировки, которая обеспечивает автоматическую компенсацию влияния моментов сил, вызванных собственной массой манипулятора. С помощью сервосистемы привода можно управлять величиной усилия, прикладываемого к рабочему объекту. В основу конструкции манипулятора положен пантографический механизм, что позволяет значительно сократить объем вычислений, необходимых для расчета моментов в шарнирах, и координат захвата. Общая схема манипулятора показана на рис. 3.68.

^* (Научно-исследовательский центр проблем механики.)

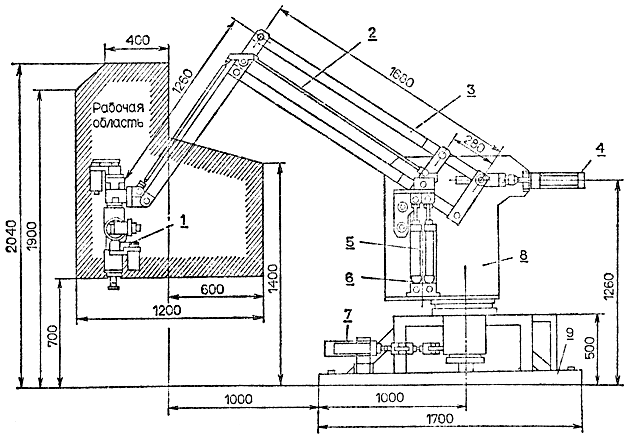
Рис. 3.68. Устройство манипулятора с силовым управлением. (Вид сбоку, 'Адаптивный робот' д-ра Идо.) 1 - механизм запястья: 2 - звено для коррекции конфигурации манипулятора на основании силовой информации; 3 - пантографический механизм; 4 - привод для управления поступательным движением в горизонтальной плоскости; 5 - привод для балансировки конструкции с учетом усилия, развиваемого захватом; 6 - привод для управления поступательным движением в вертикальной плоскости; 7 - привод для управления вращением корпуса; 8 - вращающийся корпус; 9 - неподвижное основание

Поясним основные принципы работы системы управления величиной прикладываемого усилия с помощью рис. 3.69. Трубопровод, соединяющий источник рабочей жидкости (область высокого давления) и потребителя рабочей жидкости (область низкого давления), включает в себя две узкие трубки жиклера переменного диаметра. Между жиклерами присоединено ответвление от трубопровода к гидроприводу. До тех пор пока оба жиклера находятся в открытом состоянии, рабочая жидкость циркулирует по трубопроводу. Изменяя соотношение диаметров верхнего и нижнего жиклеров, можно получить любую заданную величину выходного усилия, развиваемого гидроприводом.

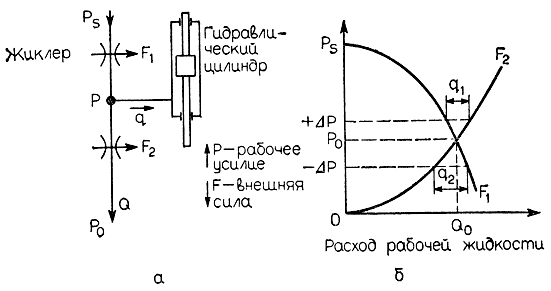
Рис. 3.69. Основной элемент системы управления рабочим усилием. а - принцип работы; б - рабочая характеристика

Если требуется, чтобы развиваемое усилие было в точности равно усилию, которое оказывает на привод внешняя нагрузка, то необходимо, чтобы количество жидкости, протекающей через каждый из жиклеров, было одинаковым (рис. 3.69, б). В этом случае разность между входным и выходным давлением рабочей жидкости в приводе становится равной нулю, и привод удерживается в статическом равновесии. Следовательно, между объемом Q₀ рабочей жидкости, протекающей через жиклер в единицу времени, и величиной заданного рабочего давления р₀ в данный момент выполняются следующие соотношения:

где Q₀ - расход рабочей жидкости в равновесном состоянии, р₀ - заданное рабочее давление, р_s - давление источника, ρ - плотность рабочей жидкости, F₁ - площадь сечения жиклера, расположенного в области высокого давления, F₂ - площадь сечения жиклера, расположенного в области низкого давления.

Допустим теперь, что величина давления нагрузки р несколько изменилась и стала равной, например, р = р₀ - Δр. Тогда расход Q₁ рабочей жидкости через жиклер высокого давления возрастает по сравнению с расходом Q₂ через жиклер, расположенный в области низкого давления. Возникающая разность Δq объемов втекающей и вытекающей жидкости поступает во входное отверстие гидропривода. Величина объема жидкости, направленной в привод, определяется по формуле

В результате поршень из равновесного состояния придет в движение со скоростью V, а величина выходного усилия, развиваемого приводом, станет равной Р. Значения Р и V определяются следующими выражениями:

Рассматриваемая система управления рабочим давлением гидропривода обладает возможностью автоматической регулировки положения поршня в соответствии G текущим значением величины давления нагрузки. Так как такая система управления давлением не содержит подвижных частей, то анализ распределения давления в реальной сервосистеме гидропривода может быть выполнен вышеизложенным способом, но с учетом вихревых потерь. Необходимость балансировки собственного веса звеньев манипулятора особенно остро проявляется при высоких давлениях нагрузки. В системе управления давлением (рис. 3.69), состоящей из пары жиклеров, величина внутренней податливости dg/Δp оказывается весьма небольшой; скорость срабатывания V/Δp также имеет неудовлетворительно низкое значение.

Чтобы преодолеть указанные недостатки, была разработана усовершенствованная система управления давлением, принцип работы которой иллюстрируется на рис. 3.70. В этой системе жиклер, расположенный в области низкого давления (рис. 3.69), заменен разгрузочным клапаном. Как следует из рис. 3.70, б, внутренняя податливость системы (угол а) улучшается. Скорость срабатывания системы управления приводом определяется следующим выражением:

Так как площадь А рабочей поверхности поршня остается неизменной, скорость срабатывания тоже увеличивается.

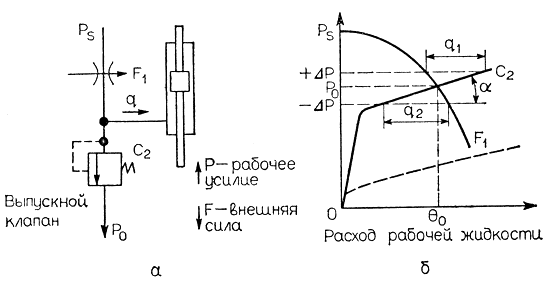
Рис. 3.70. Система управления рабочим усилием захвата (с балансировкой собственного веса звеньев манипулятора)

С помощью этого манипулятора легко можно выполнять такие операции, как установка прямоугольных предметов в угол (рис. 3.71), вращение рукоятки и т. п. Причем все управляющие алгоритмы в этом случае оказываются чрезвычайно простыми. Используя этот робот для выполнения типовых сборочных операций, Идо попытался полностью формализовать работу рук человека.

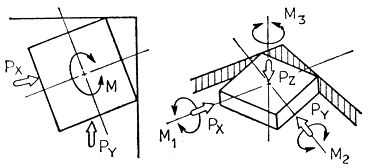
Рис. 3.71. Упаковка прямоугольных предметов с применением силового управления

Манипулятор с непосредственным управлением приводами

Самым идеальным способом управления манипулятором является непосредственное использование рабочей характеристики силомоментного электродвигателя. Другими словами, в идеальной сервосистеме изменение выходного значения развиваемого двигателем момента сил оказывается строго пропорциональным соответствующему изменению входной величины силы тока или напряжения. Рабочая характеристика обычного сервомотора постоянного тока является весьма близкой к характеристике идеального силомоментного электромотора. Однако, поскольку мощность выходного сигнала серводвигателя постоянного тока обычно невелика, для обеспечения требуемой величины выходного момента, как правило, приходится вместе с серводвигателем устанавливать редуктор скорости с понижением порядка 1:100. В то же время силомоментные двигатели за счет использования специальных магнитных материалов на основе интерметаллических соединений самарий-кобальт могут, развивать очень большой крутящий момент. Следовательно, этими двигателями можно управлять при значительно более низких скоростях вращения вала, обеспечивая при этом большую точность.

Д-р Асада применил такие силомоментные двигатели из специальных материалов при разработке одного из первых в мире безредукторных манипуляторов с непосредственным управлением приводами. Устройство этого манипулятора показано на рис 3.72. Исполнительный механизм с непосредственным управлением не подвержен вредным влияниям люфтов, которые характерны для механизмов с зубчатыми понижающими передачами. С этой точки зрения манипуляторы с непосредственным управлением приближаются к совершенным, в которых необходимая величина выходного момента обеспечивается только за счет двигателей. На рис. 3.73 показано устройство шарнира с силомоментным двигателем. К сожалению, в реальном случае величина выходного момента силомоментных двигателей оказывается все-таки слишком небольшой. В частности, установленные в манипуляторе CMU Arm силомоментные двигатели едва справляются с перемещением самого манипулятора без какой-либо нагрузки. Кроме того, нельзя не отметить некоторую конструктивную диспропорцию этого манипулятора - плечевое звено имеет внушительные размеры, в то время как локтевое звено очень тонкое.

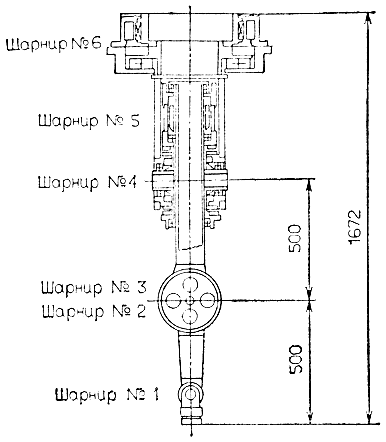
Рис. 3.72. Декартовый манипулятор с непосредственно управляемыми приводами

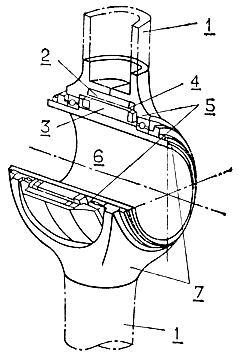
Рис. 3.73. Устройство шарнира с непосредственным управлением. 1 - звено манипулятора; 2 - статор; 3 - ротор; 4 - щетки коллектора; 5 - вложенная поверхность; 6 - ось вращения шарнира; 7 - охватывающая поверхность

По-видимому, можно считать, что первый в мире робот с непосредственным управлением приводами был разработан в 1978 г. в Научно-исследовательской лаборатории механики под руководством доктора Накано и доктора Кицуно. Этот робот имеет антропоморфный манипулятор типа MELARM-II, все степени подвижности которого управляются гидравлическими сервосистемами. Его грузоподъемность 10-15 кг. Робот обладает возможностью силового управления. Кроме того, каждый из шарниров оснащен силомоментными датчиками. Силовое очувствление обеспечивает дополнительную функциональную гибкость. Другими словами, все приводы манипулятора MELARM-II управляются двухсторонними сервосистемами, для которых управляемой и задающей величинами являются моменты сил. Общий вид манипулятора MELARM-II показан на рис. 3.74.