Обучение

Понятие "обучение"

Расширение функциональных возможностей робота сопряжено с очень сложной и трудоемкой разработкой программного обеспечения, необходимого для реализации этих функций. В этой связи представляется перспективным наделить робот способностью к обучению и тем самым повысить уровень сложности решаемых задач и расширить функциональные возможности благодаря восприятию опыта человека.

Возможность наделить машину способностью к обучению, являющейся одной из наиболее характерных особенностей высокоорганизованных существ, и в первую очередь человека, находится в центре внимания многочисленных исследователей со времени появления ЭВМ. Однако, к сожалению, приходится констатировать, что все попытки создать такую машину пока безуспешны. Объясняется это, в частности, тем, что в проблеме обучения имеются многоуровневые ограничения, вызванные в первую очередь недостаточно ясным пониманием способности к обучению высокоорганизованных существ и человека.

Исследования по обучению до сих пор развивались в рамках психологии. Приведем одно из определений понятия "обучение" в психологии. Обучение - это изменение внешнего проявления поведенческой активности, формирующееся на основании определенного опыта. Способность к обучению является у человека врожденной. Даже крыса, кошка, собака способны в определенной степени к обучению, и в то же время эта способность отсутствует у технических средств, в том числе и компьютера. Следовательно, обучение и тренировка человека возможны только тогда, когда инициируются его природные, генетически заданные способности. При обучении машин необходимо начинать прежде всего с придания им способности к обучению.

Система управления с обучением^* - это система управления, характеризующаяся целенаправленным изменением поведенческой активности на основе опыта. Это определение содержит три ключевых термина - "опыт", "целенаправленность", "изменение поведенческой активности", - требующих уточнения.

^* (Автоматическая система управления со способностью к обучению.)

Опыт: в данном случае это множество хранящихся в памяти данных о первых успешно завершенных поведенческих актах (из множества совершенных в прошлом вообще); опыт влияет на последующее поведение и принятие решений.

Целенаправленность: это критерий оценки результативности функционирования системы управления с обучением, иначе говоря, достижимости цели ее функционирования.

Изменение поведенческой активности: изменение правил оценки и предсказания (планирования), формализованное представление которых задается исходя из многочисленных оценочных критериев.

Приведенное выше определение понятия "обучение" связано с установившимся представлением о наиболее сложной способности высокоорганизованных существ. В этой связи следует заметить, что по мере изучения способности к обучению в интересах робототехники возможно, что постепенно эта способность прояснится и у человека. Кстати, индуктивный логический вывод, рассмотренный в предыдущем разделе, является, по существу, операцией вывода некоторого общего правила из множества отдельных фактов, что тоже можно считать одной из форм обучения.

Впервые способность к обучению в техническом плане была рассмотрена при изучении проблемы распознавания образов. В этом случае функция классификации образов и ее параметры выбирались на основании теории обучения. Рассмотрим в качестве примера управления обучением задачу перевернутого маятника. Эта задача анализируется применительно к разработке детской двухопорной стопоходящей машины.

Управление с обучением для опрокинутого маятника

Экспериментальная установка непрерывного удерживания в вертикальном положении путем соответствующего смещения тележки опрокинутого маятника, зафиксированного относительно этой тележки с возможностью колебания в продольно-вертикальной плоскости, схематически показана на рис. 6.11.

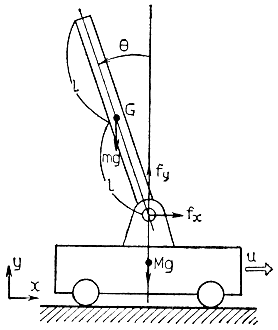
Рис. 6.11. Опрокинутый маятник на тележке

Уравнение движения этого объекта управления можно записать следующим образом:

крутящий момент относительно точки G

смещение проекции точки G на ось y

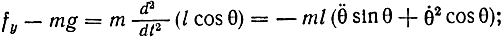
смещение проекции точки G на ось х

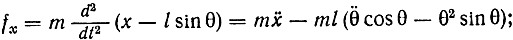
перемещение тележки (параллельно оси х)

(Здесь I - момент второго порядка в плоскости качания маятника: I - ml²/3.)

Линейная аппроксимация этих уравнений при условии управления углом θ в достаточно малой области (cos θ ≈ 1, sin θ ≈ 0, θθ^. ≈ 0, θ^.2 ≈ 0) позволяет упростить такую систему уравнений и привести ее к виду

Разрешая первое и четвертое уравнения относительно f_x и f_y, получаем

где

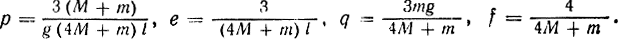
Для удерживания маятника в вертикальном положении с помощью обычной системы управления с обратной связью зададим линейную зависимость управляющей переменной и переменных состояния:

Выбрав коэффициенты обратной связи α, β, γ, δ таким образом, чтобы все характеристические корни системы по критерию устойчивости были действительны и отрицательны, обеспечим устойчивость такой системы управления в окрестности θ = θ^. = х = х^. = 0, другими словами, обеспечим удержание маятника в вертикальном положении.

Для обеспечения устойчивости такой системы управления методом управления с обучением введем предположение о допустимости упрощенного представления управляющей переменной (усилие привода тележки) и в виде двузначной функции u(t) = ±k. Переменная u взаимосвязана с крутящим моментом выходного вала двигателя привода тележки; поэтому, выбирая ее максимальную величину равной ±k, получаем оптимальное решение задачи устойчивости за минимальное время при u(t) = ±k. Тогда с учетом выражения (6.4)

где р, е - константы. Подставляя в выражение (6.5), имеем

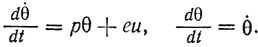
Из обоих выражений получаем

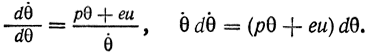
В результате интегрирования находим

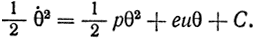
После преобразования это выражение принимает вид

Выражение (6.8) есть гипербола в плоскости θθ^.. Эта плоскость (обычно плоскость хх^.) называется фазовой плоскостью и обычно используется при исследовании динамики системы управления. На рис. 6.12 приведены траектории для обоих значений u = ±k; к сожалению, траектории лежат очень плотно друг к другу. Как следует из рисунка, для заданного u = +k (или u = -k) смещение по соответствующей траектории (в направлении, указанном стрелкой) приводит к сближению с началом координат (θ = 0 и θ^. = 0) с последующим от него удалением.

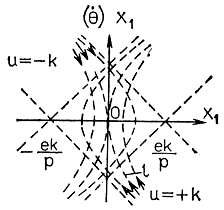
Рис. 6.12. Траектории на фазовой плоскости

Обозначим траекторию, проходящую через начало координат фазовой плоскости, через l. Тогда, чем ближе состояние системы управления к кривой l, тем ближе оно к началу системы координат, т. е. к устойчивому состоянию системы. Переместимся из некоторого состояния Р по траектории (при u = -k), приближаясь к началу координат. Если в этот момент переключить полярность управляющего воздействия на выходе двигателя на противоположную (в данном случае на u = +k), то попадаем в точку S (рис. 6.13). Следовательно, если получить граничную линию, соответствующую кривой l, такую что при этом фазовая плоскость делится на две равные части при u = +k и u = -k (рис. 6.14), можно определить устойчивое состояние (границы устойчивости) системы управления. Такая граничная линия может быть получена путем обучения.

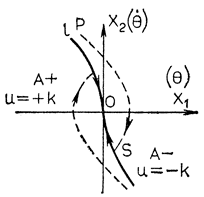
Рис. 6.13. Траектория достижения устойчивости

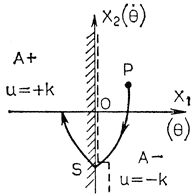
Рис. 6.14. Модификация граничной линии

В первую очередь задается граница по оси θ^.. При этом состояние (для точки Р) переключается из u = -k на u = +k в точке S. Однако в этом случае мы не приближаемся к границе устойчивости вследствие запаздывания переключения. Поэтому изменим границу так, как это показано на рисунке. Аналогичная ситуация складывается и в верхней полуплоскости. В результате многократного повторения этой операции обеспечивается последовательное приближение к требуемой границе (рис. 6.15, 6.16). Заметное искривление полученных теоретически и экспериментально граничных кривых (по мере увеличения значений θ и θ^.) вытекает из выражения (6.5) и допущения малости значений θ и θ^..

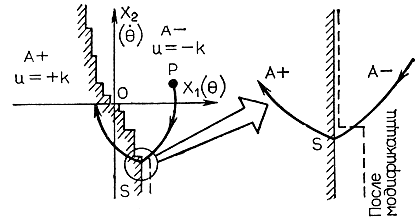
Рис. 6.15. Модификация граничной линии

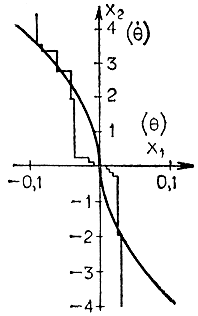
Рис. 6.16. Граничная линия

Достоинство рассмотренного выше способа управления с обучением заключается в упрощении алгоритма работы системы управления благодаря использованию управляющих таблиц, которые составляются в результате анализа сложных уравнений движения. Однако пока ничего нельзя сказать о том, до какой степени применим подобный метод в случае более сложных систем управления - с большим числом степеней свободы, какие осложнения будут иметь место в связи с требуемым объемом памяти, скоростью вычислений, способом инструктирования системы и т. д. В частности, изучение влияния детальности и точности определения граничной линии (иначе говоря, погрешности составления управляющих таблиц) на погрешность работы системы и объем требуемой памяти позволило вывести аналитические зависимости, показывающие логически обоснованный факт, что при равномерном масштабировании по оси θ детальность масштабирования по оси θ^. будет тем лучше, чем дальше от начала координат.