Принятие решения

Принятием решения в искусственном интеллекте называется решение проблемы путем поиска и абдукции. Полученное решение проблемы, являющееся с определенной степенью вероятности ее причиной (или сутью), подобно, например, решению системы линейных уравнений. Робот с высоким уровнем интеллекта должен работать по обобщенному заданию, которое поступает к нему от человека или системы управления более высокого уровня. Интеллектуальные возможности такого робота должны обеспечить разбиение порученной задачи (работы) на ряд последовательных простых операций и выбор алгоритма выполнения каждой из этих операций. Таким образом, под принятием решения понимается выбор реализуемого алгоритма осуществления роботом данной работы или отдельных операций, на которые она разбита. Следовательно, должен быть определен уровень принятия решения в зависимости от объема и степени сложности заданной работы.

Наиболее продуктивной процедурой принятия решения является дедуктивный вывод, или категорический силлогизм.

Как уже отмечалось, для обеспечения вывода необходимы данные двух типов: для большой посылки (дедуктивное правило) типа "если А, то В" и для малой посылки (фактическое заявление) типа "есть А". Эти данные называются данными о знаниях (knowledge data) или просто знаниями, и их объем должен быть достаточно представительным. Упорядоченное множество таких знаний называется базой знаний (knowledge base). На первый взгляд дедуктивное правило можно считать аналогом программы современных вычислительных машин, однако при этом важно иметь в виду совершенно различное содержание этих двух схожих процедур. Программа ЭВМ задает последовательность обработки данных, в то время как дедуктивное правило позволяет детализировать и формализовать разнообразные причинно-следственные связи явлений (процессов) и дел (предметов). Компьютер, осуществляющий принятие решения, решает проблему путем поиска соответствующего дедуктивного правила и выполнения операции дедуктивного вывода. Следовательно, дедуктивные правила - это знания, необходимые для выполнения алгоритма принятия решения, и они имеют существенно большую значимость для компьютера, чем современные программы ЭВМ.

При вводе недостоверной или неточной информации, например при распознавании образов или распознавании (переводе) текста на естественном языке, выявление и исправление этой неточности требуют привлечения всех накопленных знаний. Основная часть этих знаний закодирована не только арифметическими, но и логическими символами; поэтому требуется специальный язык для ЭВМ, ориентированный на обработку подобного рода логических символов, другими словами, язык для искусственного интеллекта.

К наиболее широко используемым языкам для искусственного интеллекта в первую очередь следует отнести язык ЛИСП, разработанный в Массачусетском технологическом институте (США). Частично используется также язык ПЛАННЕР, ориентированный на проведение поиска методом проб и ошибок.

Среди алгоритмических языков, появившихся в последнее время, внимание привлекает язык ПРОЛОГ, который стал первой законченной разработкой по широкой программе исследований проекта создания ЭВМ пятого поколения. И хотя вряд ли обосновано утверждение о его замене на язык ЛИСП, все же есть немало направлений исследований, где по-прежнему предпочтение отдается языку ЛИСП.

Во всяком случае постановка проблемы принятия решения возможна только благодаря системе базы знаний с большим объемом данных о знаниях и обеспечению поиска требуемых данных о знаниях, однако для практического составления программы принятия решения необходимо выполнить планирование. Рассмотрим в качестве примера принятия решения способ использования пространства состояний.

Примеры принятия решения с использованием пространства состояний

Задача переноса блока захватом робота

Рассмотрим проблему принятия решения на примере задачи переноса захватом манипулятора блока, находящегося в положении 2 (рис. 6.2, а), в положение 4; рабочая среда и исходное состояние соответствуют приведенным на рисунке.

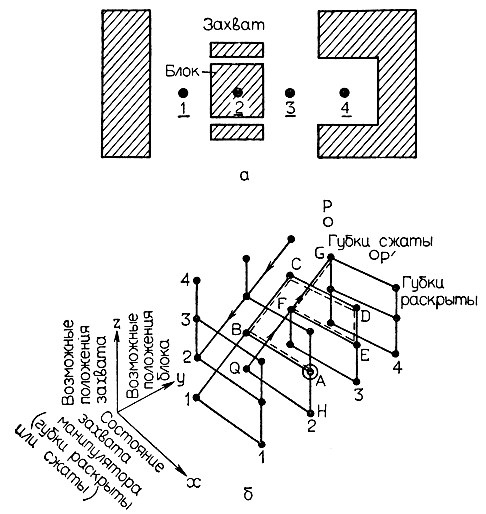
Рис. 6.2. Выполнение захватом манипулятора простой работы. a - рабочая среда; б - пространство состояния для этой работы

Захват робота не в состоянии поместить блок в положение 4 при положении захвата, показанном на рисунке, из-за недостатка свободного места. Следовательно, задача может быть решена только в результате выполнения операций последовательности, на последнем этапе которой захват поставит блок в положение 4. Захват манипулятора может выполнять только следующие операции:

● единичное смещение влево;

● единичное смещение вправо;

● раскрытие губок захвата;

● сжатие губок захвата.

Путем соответствующего сочетания этих операций можно: сжать блок губками захвата, перенести захватом блок в требуемое положение и, сжав губки захвата, поставить блок в требуемое положение. Следовательно, требуемая работа (задача, требующая принятия решения) заключается в том, чтобы, каким-либо способом переместив блок в положение 3, протолкнуть его затем до положения 4.

Сотрудники Массачусетского технологического института (США) Феррел и Шеридан предложили решение этой задачи с использованием пространства состояний, под которым понимается пространство с квантованными (дискретными) значениями состояния (значения по каждой оси), путем возможных сочетаний положения блока и состояния захвата (губки раскрыты или сжаты).

Обозначим в пространстве состояний (рис. 6.2, б) по оси у возможные положения блока 1, 2, 3, 4, по оси z аналогичные положения захвата 1, 2, 3, 4, по оси х состояние захвата манипулятора: губки раскрыты или сжаты. Допустим, что исходное состояние соответствует приведенному на рис. 6.2, а: блок и захват находятся в положении 2, губки захвата раскрыты, что соответствует положению 2 на оси х (точка А на рис. 6.2, б). В этом пространстве состояния есть точки, не имеющие права на существование, например точки Р и Р' (одновременное, совместное нахождение в положении 4 блока и захвата)^*.

^* (Эти точки, а также нереализуемые состояния типа положение 4 при раскрытых губках захвата, на схеме пространства состояний не помечены черными кружками.)

Как уже отмечалось, имеются только четыре стандартные команды, которые выполняет манипулятор: раскрытие, сжатие (губок захвата), движение вправо, движение влево. Комбинируя эти команды соответствующим образом, в пространстве состояний можно представить в виде перехода из некоторой точки в смежную даже такие операции, как сжатие захватом блока и его перенос.

В пространстве состояний имеют место и нереализуемые ситуации, например, при прямом переходе из точки 1 в другие смежные точки. Из точки Q, когда блок находится в положении 2, а захват - в положении 1 (губки сжаты), невозможен переход в точку В (Q → В), когда блок остается в прежнем положении (губки захвата остаются сжатыми), а захват переходит в положение 2. При выполнении этой операции захват вытолкнет блок в положение 3, что будет означать операцию Q → F.

И наоборот, при переходе из точки F в точку 1 при сжатых губках захвата нельзя попасть в точку Q. В этом случае получается переход в точку R, поскольку блок неподвижен. Практически невозможен также прямой переход из точки F в точку Q. Иначе говоря, в отдельных случаях имеются однонаправленные переходы, когда обратный переход в исходное состояние невозможен (такие случаи отмечены сплошной линией со стрелкой). Как следует из рис. 6.2, а, работа по переносу блока из исходного положения в положение 4 может быть выполнена в следующей последовательности. Прежде всего сжимаются губки захвата и блок переносится в положение 3. Затем губки раскрываются, захват возвращается в положение 2, губки сжимаются и захват вновь переходит в положение 3. В результате находящийся в этом положении блок вытесняется в положение 4. В пространстве состояний этой процедуре соответствует последовательность А → B → C → D → E → F → G (рис. 6.2, б).

Как следует из рис. 6.2, б, переход из исходной точки А в конечную точку G возможен и по другим маршрутам, например последовательность A → H → Q → F → G. Если эту последовательность представить в виде реальных операций (рис. 6.2, а), получим следующую процедуру: захват исходного состояния (губки раскрыты) переходит в положение 1 (а), затем губки захвата сжимаются (Н) и в этом состоянии захват перемещается, проталкивая перед собой блок до положения 3 (Q). В заключение блок вдвигается в положение 4 (F). Разумеется, можно также выбрать другие, отличные от рассмотренных последовательности выполнения работы.

Такого рода простая манипуляционная операция может быть представлена во взаимосвязи со всеми возможными состояниями, их переходами, стоимостями каждого перехода, исходного и конечного состояний. При этом возникает задача выбора минимального пути (минимальной стоимости в широком смысле), когда выявляется не менее двух возможных путей достижения конечной точки в пространстве состояний.

Способ выбора траектории с минимальной стоимостью показан на рис. 6.3. В первом приближении решение этой задачи получают в виде последовательности минимальных стоимостей, соответствующих переходам из состояний, смежных с крайне левым верхним состоянием (прослеживаются состояния последовательно по вертикали, сверху вниз). Для состояния В возможны три варианта перехода: А → В, С → В, Е → В. Стоимости этих переходов: 0 + 4 = 4, ∞ + 1 = ∞, ∞ + 1 = ∞ соответственно. В результате для минимальной стоимости - четыре - получаем переход А → В. Затем для состояния В имеем шесть возможных вариантов перехода с минимальной стоимостью два, соответствующей переходу В → С. При этом была использована стоимость состояния В. Действуя подобным образом, получаем картину стоимостей и последовательность переходов в первом приближении (рис. 6.3, б), затем во втором приближении на основе значений, полученных в первом приближении. Эта процедура повторяется до тех пор, пока результат не станет неизменным с каждым новым приближением. В результате получаем путь минимальной стоимости A → C → B → F → D (рис. 6.3, г). На рис. 6.3, д, в приведены результаты первого и второго приближений при переборе состояний по горизонтали, начиная с верхнего левого. Описанная процедура аналогична релаксационному методу, широко используемому для получения численного решения на ЭВМ.

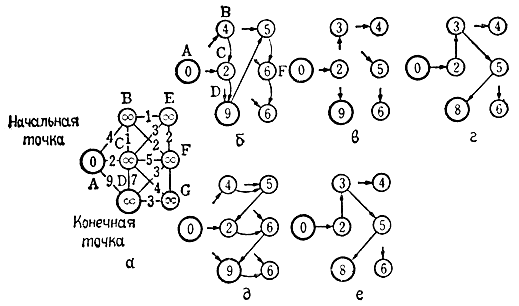
Рис. 6.3. Способ вычисления сходимости для получения минимальной траектории. б - первое приближение; в - второе приближение; г - третье приближение

Задача: вынести софу из комнаты

Предположим, что на ограниченной площади расположены различные предметы, в том числе длинный предмет прямоугольной формы. Требуется вынести этот предмет за пределы данной площади (рис. 6.4). Например, можно представить эту задачу как задачу перемещения находящейся в комнате софы. При этом важное значение имеет положение (или ориентация) софы относительно окружающих ее предметов (окружающей среды). Введем три переменные, характеризующие положение (состояние) софы на плоскости (координатные оси пространства состояния):

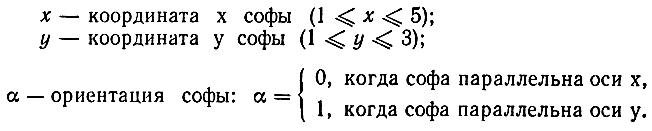
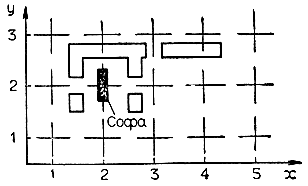
Рис. 6.4. Физическое пространство для решения задачи о перемещении софы

Захват манипулятора может выполнять следующие команды позиционирования:

● единичное перемещение вдоль оси х (в оба направления);

● единичное перемещение вдоль оси у (в оба направления);

● разворот на 90°.

Эти три команды определяют дискретность положения (и ориентации) софы; иначе говоря, положения, которые может занимать софа, соответствуют только точкам пересечения двух линий (рис. 6.4), а ее ориентация совпадает с какой-либо из этих линий. Комната имеет широкую и узкие двери, причем вынос софы через узкие двери возможен только при условии, что софа строго перпендикулярна плоскости стены с дверью (рис. 6.5).

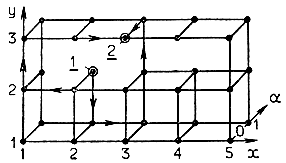
Рис. 6.5. Минимальный путь и пространство состояний по рис. 6.4

Допустим, что в этом пространстве состояний каждое единичное линейное перемещение (стоимость в широком смысле) софы равно двум, а угловое перемещение (стоимость) - трем. Исходным состоянием является положение (2, 2) с ориентацией параллельно оси у, а конечным состоянием - положение (3, 3) с ориентацией параллельно оси х. В пространстве состояний им соответствуют точки (2, 2, 1) и (3, 3, 0).

Решение задачи поиска минимального пути (минимальной стоимости) перемещения софы случайно дало два идентичных по стоимости варианта (рис. 6.5 и 6.6). На первый взгляд может показаться, что минимальным является путь из точки (2, 2) в точку (3, 3), однако это не верно, поскольку в этом случае имеет место трехкратный разворот софы на 90° (стоимость каждой такой операции равна трем).

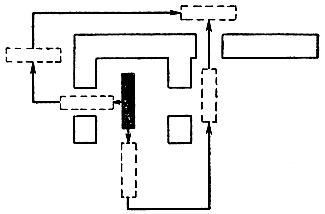
Рис. 6.6. Минимальный путь в физическом пространстве

Существенной особенностью рассмотренной выше модели пространства состояний является ее дискретность. Плотность его квантования (дискретизации) определяется исходя из набора основных команд позиционирования, необходимых и достаточных для выполнения заданной работы. Завышение числа значений по каждой координате пространства состояний нецелесообразно из практических соображений - с его увеличением резко возрастает число возможных состояний, причем настолько, что оказывается невозможным выполнение соответствующих вычислений на ЭВМ. Например, при шести переменных состояния и десяти возможных значениях по каждой переменной пространство состояний содержит 10⁶ точек. Таким образом, даже при незначительном усложнении работы пространство состояний становится слишком большим, и в этом заключается основной недостаток метода пространства состояний.

Рассмотрим метод разбиения исходной задачи на несколько подзадач, с тем чтобы выбор минимального пути решения подзадач достижения промежуточных целей оказался реализуемым на ЭВМ.

Способ задания промежуточных целей

Рассмотрим следующую задачу: объект А требуется перенести через узкий проход, около которого находится объект В, мешающий выполнению этой работы. Следовательно, прежде всего надо передвинуть объект В в положение, при котором он не будет загораживать проход, и только после этого можно будет переносить объект А (рис. 6.7).

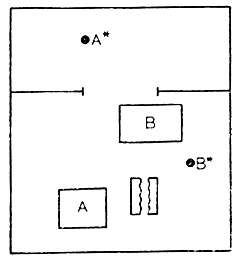
Рис. 6.7. Работа по перемещению объекта А в положение А^*

Полностью автоматическое планирование выполнения такой работы при заданных только исходном и конечном состояниях сопряжено с анализом пространства состояний большой размерности. Например, при ограничении только десятью значениями по каждой из двух координат х, у для манипулятора объекта А и препятствия В соответственно общее число состояний, включая также в рассмотрение операции раскрытия и сжатия губок захвата, будет (2 × 10 × 10) × (10 × 10) × (10 × 10) = 2·10⁶ точек.

Если наблюдатель-супервизор (человек или ЭВМ) представит эту задачу в виде двух последовательно выполняемых подзадач типа "перенести препятствие В в положение В^*" и "перенести объект А в положение А^*", можно ограничиться анализом пространства состояний, содержащим (2 × 10 × 10) × (10 × 10) = - 2·10⁴ точек. В результате число точек состояний сокращается в 100 раз. Увеличивая число соответственно выбранных подзадач, можно еще сократить объем вычислений. Например, обозначим центральную точку прохода через С и зададим следующую последовательность подцелей: "Передвинуть препятствие В в положение В^*", "Передвинуть объект А в положение С" и "Передвинуть объект А в положение А^*". В этом случае работа манипулятора и окружающая его среда существенно упрощаются, поэтому не требуется даже десяти значений для каждой переменной х, у; при этом резко сокращается и общее число точек состояния.

Следовательно, разбиение исходной задачи на последовательность подзадач позволяет исключить основной недостаток метода пространства состояний (резкое возрастание точек состояния при анализе и планировании сколько-нибудь сложной работы), причем разбиение осуществляет человек, в то время как выбор минимального пути достижения каждой подцели выполняет ЭВМ. Считается, что такой метод управления роботами и манипуляторами, получивший название метод супервизорного управления, окажется весьма эффективным^*.

^* (Этот метод называется также телеоператорным методом.)

Метод дерева "или"

Для решения задачи поиска минимального пути в сложном пространстве состояний, подобном рассмотренному выше, было предложено использовать метод дерева или либо метод дерева и.

Прежде всего заметим, что команды, выполняемые манипулятором для решения рассматриваемой задачи, есть функции переменных (этими переменными являются наименования объекта и положения), причем значение этих функций, указывающих путь в пространстве состояний, не является единственным (имеет несколько путей в этом пространстве). Например, команда TAKE имеет вид

TAKE (А, X, Y) - перенести объект А в положение X, захват должен остановиться в положении Y. (6.1)

Команда SWITCH (поменять местами A и В) может быть определена через команду TAKE следующим образом:

Здесь символ + означает последовательность операций; X - соответствующее положение между А, В, которое указывается оператором; Y - положение в окрестности X; А', В' - положение в окрестностях А, В.

Операция SWITCH может быть адаптирована к используемой ЭВМ и позволяет осуществить замену вышеуказанных X^-, Y^- на более широкие области X, Y:

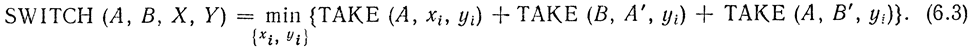
Здесь {x_i}, {y_i} - множество положений в области X, y. Для получения результата на основе (6.3) необходимо построить дерево, указывающее множество путей, которые могут быть найдены с помощью выбора в качестве подзадач соответствующих x_i, y_i. Рассмотрим в качестве примера дерево или для случая, когда имеется по два положения в каждой области: x₁, x₂ в области X^- и y₁, y₂ в области Y^- (рис. 6.8). Стоимость в этом случае вычисляется аналогично рассмотренному выше примеру (рис. 6.5). В результате получаем необходимый минимальный путь выполнения операции.

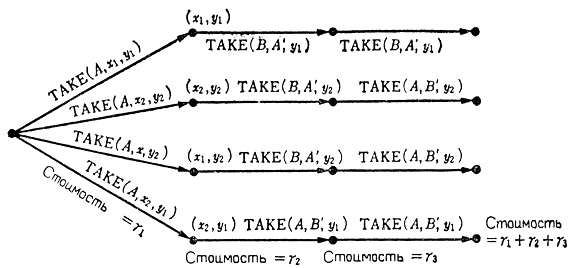
Рис. 6.8. Дерево "или" для получения численных значений с помощью выражения (6.3)

Исходя из возможных для X¯, Y¯ сочетаний x_i, y_i и используя соотношение (6.3), выбирают х, y с минимальной стоимостью. При выборе эффективных точек из выражения (6.2) для выражения (6.3) следует иметь в виду, что от оператора не требуется точного задания координат для X¯, Y¯. На практике это может быть осуществлено оператором световым пером на экране графического дисплея с изображением рабочей среды.

На рис. 6.9 показан пример рабочей операции, аналогичной приведенной на рис. 6.7, но с двумя препятствиями. Объект А требуется переместить в положение X через узкий проход, загороженный двумя объектами - В₁, В₂. Для решения задачи сначала надо устранить препятствия, т. е. переместить объекты В₁ и В₂ в другое место, и только после этого переносить объект А. Используя дисплей, оператор дает роботу команду типа: "Это препятствия; здесь область, в которую их можно поместить; затем перенести объект А в положение X".

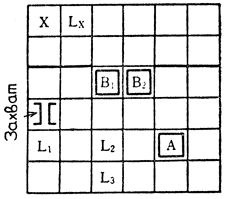
Рис. 6 9. Физическое пространство в задаче с препятствиями у прохода. В₁, В₂ - препятствия; L₁, L₂, L₃ - местоположения препятствий; X - конечное (целевое) положение объекта А; L_X - конечное положение захвата

Дерево "или" для этой работы аналогично рассмотренному на рис. 6.10. Захват может начинать работу по любому из трёх путей: 1 сначала захватить либо объект А, 2 либо препятствие В₁, 3 либо препятствие В₂.

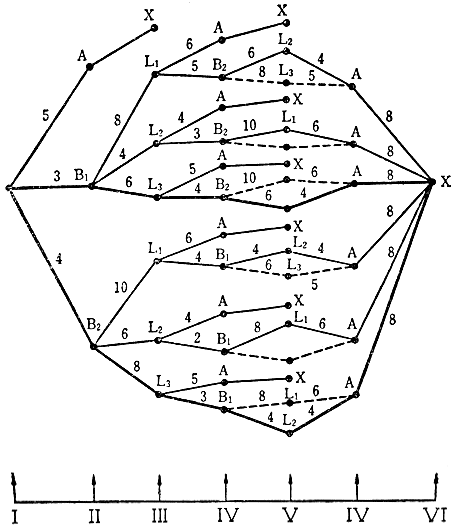
Рис. 6.10. Решение по дереву 'или'. ^____ оптимальный путь; --- сокращенный участок пути в процессе минимизации; I - начало; II - поиск объекта; III - поиск местоположения; IV - объект; V - местоположение; VI - конечное (целевое) местоположение объекта

1 При попытке переноса объекта А у прохода становится слишком тесно.

2 Попытка переноса препятствия В₁ приведет к трем вариантам его размещения: в положения L₁, L₂, L₃. За этим шагом следует выбор одного из следующих вариантов: перенос объекта А или препятствия В₂, в результате которого выясняется, что для переноса объекта А проход по-прежнему тесен.

3 При переносе препятствия В₂ имеется выбор одного из возможных вариантов; размещение препятствия в любое из оставшихся двух местоположений. После отработки любого из этих вариантов объект А переносится в положение X. Определим стоимости соответствующих этим вариантам путей при допущении, что диагональные перемещения исключаются. При этом стоимость единичного перемещения захвата без груза принимаем равной единице, а стоимость единичного перемещения захвата с объектом - равной двум. В результате получаем путь минимальной стоимости, отмеченный на рисунке толстой сплошной линией.