2.2. Формализация задачи построения и оптимизация программных движений роботов

Формализация и решение задачи гибкого автоматического программирования РТК связаны с большими трудностями. Дело в том, что в процессе программирования РТК нужно не только построить ПД отдельных единиц оборудования РТК (роботов, станков и т. п.), но и обеспечить их взаимную координацию и синхронность, диктуемую ритмом и характером заданного технологического процесса. Фактически общая задача гибкого программирования РТК распадается на две задачи:

1. индивидуальное (персональное) программирование роботов и технологического оборудования;
2. групповую координацию (диспетчеризацию) построенных ПД.

Наибольшие осложнения возникают при постановке и решении первой задачи. Продемонстрируем основные трудности на примере автоматического программирования движений манипуляционного робота. Исполнительным механизмом такого робота является манипулятор вместе с рабочим органом (механизм захвата, измерительный щуп и т. п.). Управление звеньями манипулятора и рабочим органом осуществляется с помощью сил и моментов, вырабатываемых системой приводов робота. Для формирования требуемых управляющих воздействий необходимо прежде всего построить ПД манипулятора. Перейдем к строгой формулировке этой задачи.

Рассмотрим манипулятор, имеющий т степеней свободы. Его конфигурация в произвольный момент времени t задается m-мерным вектором управляемых координат 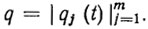Положение рабочего органа r однозначно определяется по заданной конфигурации манипулятора с помощью уравнения кинематики вида

Движение под действием вектора управляющих сил или моментов 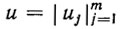описывается уравнением динамики вида

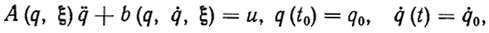(2.2)

где и - скорость и ускорение изменения q(t), ξ, р- мерный вектор параметров; A (q, ξ), b (q, 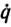, ξ) - заданные матрица- и вектор-функции размерности m*m и m соответственно.

Цель управления движением манипулятора, диктуемая заданным технологическим процессом, заключается либо в переводе рабочего органа в заданное положение, либо в отслеживании им заданной траектории.

Целевое условие первого типа имеет вид

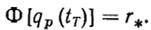(2.3)

По существу оно определяет режим наведения рабочего органа манипулятора в точку r_* в момент времени t_Т.

Целевое условие второго типа имеет вид

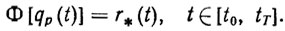(2.4)

Ему соответствует режим отслеживания рабочим органом заданной траектории r_*(t) на интервале времени [f₀, t_T].

В процессе достижения цели должны выполняться следующие ограничения и условия:

1. кинематические ограничения на управляемые координаты;
2. динамические ограничения на скорость и ускорения изменения обобщенных координат, согласованные с ограничениями на управления;
3. условия обхода манипулятором препятствий (включая условия, исключающие возможность самопересечения манипулятора).

Закон изменения управляемых координат, обеспечивающий за конечное время достижение заданной цели движения при соблюдении трех перечисленных выше, условий, будем называть программным движением (ПД) манипулятора. Обозначим этот закон через q_p(t) и определим его формально.

Программное движение q_p (t) - это дважды дифференцируемая m-вектор-функция, удовлетворяющая при всех t ∈ [t,sub>0, t_T] целевому условию вида (2.3) или (2.4) и ограничениям вида

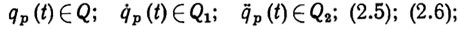(2.7)

(2.8)

где Q, Q₁, Q₂- заданные множества m-мерного пространства; M[q_p(t)] - множество точек в области достижимости D, занимаемое манипулятором в конфигурации q_p(t). Заметим, что целевая точка r_* и траектория рабочего органа r_*(t) должны всегда находиться в рабочей зоне R = D/Р, т. е. в некоторой области из D, свободной от препятствий.

Задача автоматического построения ПД манипулятора заключается в следующем. Пусть заданы кинематические и динамические уравнения (2.1), (2.2) и ограничения (2.5)-(2.7), препятствия Р, интервал времени [f₀, t_r] и целевое условие в форме (2.3) или (2.4). Требуется разработать методы и алгоритмы, обеспечивающие фактическое построение ПД по указанным данным. Очевидно, что если требуемое ПД построено, то оно будет технологически приемлемым.

Сформулированная задача может иметь много решений, среди которых целесообразно выбрать наилучшее, т. е. оптимальное ПД. Для этого в классе рассматриваемых ПД определим функционал качества вида

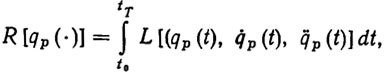(2.9)

где L - некоторая заданная функция, выбираемая из условия, что функционал (2.9) характеризует затраты на осуществление ПД q_p(t).

Задача оптимизации сводится к выбору такого ПД q⁰_p(t), при котором функционал (2.9) принимает наименьшее возможное значение, т. е.

ПД q⁰_pt∈[t₀,t_T] удовлетворяющее критерию оптимальности (2.10), будем называть оптимальным. Такое движение задает оптимальный режим функционирования манипуляционного робота. Например, если L (q_p картинки )≡1, то получаем режим наибольшего быстродействия. В этом случае

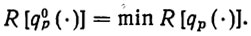(2.11)

и оптимальное ПД минимизирует время (2.11) выполнения технологической операции. Осуществление такого режима работы обеспечивает наивысшую производительность робота при заданных ограничениях.

Таким образом, оптимальное программирование движений манипулятора заключается в построении оптимального ПД, удовлетворяющего критерию качества (2.10).

Решение задач построения и оптимизации ПД сопряжено с большими трудностями. Эти трудности порождены нелинейностью и высокой размерностью уравнений кинематики и динамики (2.1), (2.2), наличием препятствий (2.8) и конструкционных ограничений (2.5)-(2.7). Кроме того, в случае целевого условия (2.3) возникает необходимость решать двухточечную краевую задачу, которая резко усложняется при оптимизации ПД в смысле критериев (2.9)-(2-11).

Для манипуляционных роботов характерно, что траектория рабочего органа строится (и наблюдается) в рабочей зоне, а отвечающее ей ПД синтезируется в пространстве конфигураций. Высокая размерность этого пространства (m> 6) обуславливает кинематическую избыточность манипулятора. И хотя эта избыточность полезна - благодаря ей увеличивается маневренность манипулятора, расширяются возможности его адаптации к препятствиям - она еще больше усложняет задачу автоматического программирования движений.

Применительно к манипуляционным роботам значительные трудности связаны также с тупиковым ситуациями, обусловленными структурой множества кинематических ограничений Q и препятствий Р. Наличие тупиковых ситуаций приводит, в частности, к тому, что не для всякой траектории рабочего органа r_*(t), целиком лежащей в рабочей зоне R> существует соответствующее ей непрерывное ПД q_p(t). Для распознавания тупиковых ситуаций и поиска путей их обхода необходимы дополнительные средства анализа и планирования движений. Эти алгоритмические средства обеспечивают своеобразную адаптацию ПД к тупиковым ситуациям и препятствиям.

Аналогичным образом формируется задача автоматического программирования и оптимизации движений транспортных роботов. Однако эта задача имеет свою специфику, связанную главным образом с тем, что в роли исполнительного механизма здесь выступает колесное или гусеничное шасси.

Особенности конструкции транспортных роботов порождают специфический характер уравнений кинематики и динамики [вместо голономной связи (2.1), присущей манипуляционным роботам, здесь возникает неголономная связь, определяемая типом шасси] и ограничений (например, появляются новые ограничения, описывающие условия опрокидываемости шасси при поворотах на больших скоростях). Поскольку промышленные транспортные роботы функционируют в производственной обстановке, где оборудование ГАП зачастую выступает как препятствие, возникает необходимость предварительной прокладки безопасного маршрута транспортировки грузов с целью предотвращения столкновений.

Решение этой задачи, включая оптимизацию маршрута, представляет собой первый этап гибкого программирования движений транспортных роботов. На втором этапе по заданному маршруту (который по построению является технологически приемлемым и безопасным) строится само ПД шасси с учетом имеющихся кинематических и динамических ограничений. Методы и средства для автоматического программирования и оптимизации движений транспортных роботов в условиях ГАП излагаются в гл. 6.