2.3. Алгоритмы определения положения исполнительных механизмов и рабочих органов

Конфигурация исполнительного механизма робота определяется m-мерным вектором обобщенных координат q. Зная q, можно определить положение и ориентацию отдельных звеньев механизма и рабочих органов. Задачи такого рода называются прямыми задачами о положении механизмов РТК.

Необходимость в решении прямой задачи в робототехнике возникает в связи с тем, что текущие положение и ориентация некоторых звеньев исполнительного механизма (например, захвата манипулятора) зачастую не могут быть определены путем прямых измерений. Вместо этого имеется возможность точно измерить относительные положения звеньев, например, с помощью позиционных датчиков обобщенных координат. По этим данным можно вычислить положение и ориентацию всех звеньев, в том числе и рабочих органов.

Рассмотрим особенности решения прямой задачи для манипуляционных роботов. В роли обобщенных координат q_j, j= 1,…, m манипулятора обычно выступают углы между звеньями или длина звеньев с. Поэтому вектор обобщенных координат у манипулятора с вращательными и поступательными кинематическими парами имеет компоненты

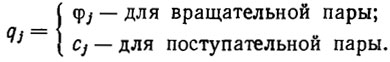(2.12)

Тип кинематической схемы манипулятора задается m-мерным вектором σ с компонентами

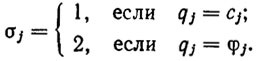(2.13)

По вектору обобщенных координат q однозначно определяется положение и ориентация всех звеньев манипулятора. Свяжем с j-м звеном правую ортогональную локальную систему координат с началом в точке r_j и ортами е^j₁, e^j₂, е^j₃, причем r_j расположим на кинематической оси (j-1)-го и j-го звеньев, а орт е¹₃ направим по этой оси. Будем считать, что система координат стойки манипулятора совпадает с абсолютной неподвижной системой координат, т. е. формула 3

Каждому звену манипулятора поставим в соответствие матрицу размерности 3*4 следующего вида:

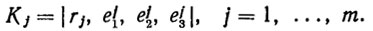(2.14)

Геометрический смысл матрицы K_j ясен из ее структуры: первый столбец характеризует положение j-го звена в абсолютной системе координат 0d₁d₂d₃ (точнее, положение начала j-й локальной системы координат, связанной с j-м звеном), а три остальных ориентацию j-го звена. Очевидно, что матрица K_j однозначно определяет положение j-го звена манипулятора в рабочем пространстве, поэтому матрица (2.14) называется матрицей кинематических характеристик манипулятора [66].

Выразим элементы матрицы кинематических характеристик через обобщенные координаты механизма. Это позволит по единой формуле экономно вычислять положение и ориентацию всех звеньев манипулятора непосредственно по его обобщенным координатам.

Введем для краткости записи следующую операцию произведения 3*4-матриц K_i = (r_i, E_i), K_j=(r_j, E_j):

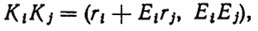(2.15)

а также 3*4-матрицы преобразований [66]

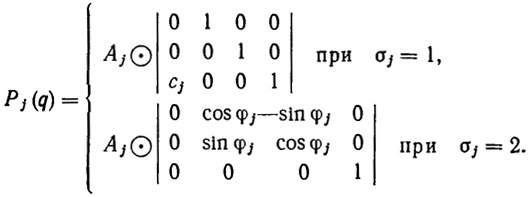(2.16)

Здесь A_j - 3*4 - матрицы вида

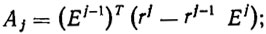(2.17)

Т - символ транспонирования. Матрицы (2.17) формируются заранее в исходном положении манипулятора, т. е. при q=0.

При этих обозначениях матрицы кинематических характеристик определяются рекуррентными формулами

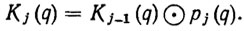(2.18)

Выберем на j-м звене некоторую точку r^j_*. Обозначим через d^j_* вектор координат этой точки в локальной системе координат r_je^j₁e^j₂e^j₃. Тогда положение точки rj* определяется формулой

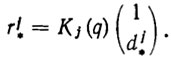(2.19)

На практике часто требуется знать положение некоторой характеристической точки r_* на захвате манипулятора. Оно однозначно определяется уравнением кинематики (2.1), где

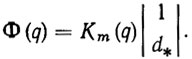(2.20)

Значительный интерес для программирования движений роботов представляет и обратная задача о положении механизма. Эта задача заключается в определении обобщенных координат q, определяющих возможные конфигурации исполнительного механизма по заданным положению и ориентации некоторых его звеньев. Например, для манипуляционного робота часто требуется по заданному положению схвата r_* найти отвечающие ему векторы обобщенных координат q, т. е. нужно решить уравнение кинематики (2.1).

Различные алгоритмы решения обратной задачи о положении манипулятора при m≤ 6 описаны в работах [32, 42, 88]. Они решают уравнения (2.1) "в лоб". Это позволяет выделить в явном виде конечное число ветвей решения уравнения (2.1). В ряде случаев (например, при наличии препятствий в рабочей зоне) для увеличения маневренности манипулятора нужна определенная кинематическая избыточность. Это достигается увеличением степеней свободы манипулятора так, чтобы было т>6. Появились даже гибкие манипуляторы типа "хобот", у которых т>10. Для таких манипуляторов с большой кинематической избыточностью нужны методы решения уравнений (2.1), ориентированные на использование ЭВМ.

Ряд методов решения обратной задачи о положении основывается на сведении решения уравнения (2.1) и минимизации функционала вида [42, 50, 67, 88 ]

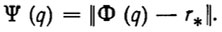(2.21)

Этот функционал обладает следующими свойствами:

1. Ψ (q) -непрерывно дифференцируемая функция, причем Ψ (q)≥ 0;
2. если градиент Δ Ψ (q) = 0, то Ψ (q) = 0 (здесь Δ Ψ= ∂Ψ/ ∂q).

Содержательно Δ Ψ (q) означает расстояние между целевой точкой r* и положением захвата r=Ф(q) в конфигурации q.

Рассмотрим кратко некоторые методы минимизации функционала (2.21). Зафиксируем целевую точку r_* и начальное приближение q⁰. Тогда градиентный метод минимизации будет заключаться в построении минимизирующей последовательности q⁰, q¹,q² по правилу

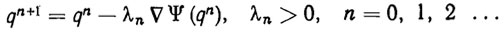(2.22)

Параметр λn называется длиной шага в направлении антиградиента - ΔΨ(qⁿ). Если Δ Ψ (qⁿ) ≠0, то шаг λ_n можно выбрать так, чтобы Ψ(qⁿ⁺¹)<Ψ (qⁿ). Если Δ Ψ(qⁿ)=0, то Ψ(qn)=0 и процесс (2.22) прекращается.

В зависимости от способа выбора шага λ_n можно получить различные варианты градиентного метода. Так, если λ_n выбирать из условия оптимальности

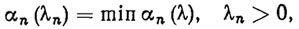(2.23)

где α_n=Ψ[qⁿ-λΔΨ(qⁿ)], λ ≥0, то придем к методу наискорейшего спуска [28]. Этот метод имеет простой геометрический смысл: точка qⁿ⁺¹ лежит на луче ln ={q:q =qⁿ-λ Δ Ψ (qⁿ),λ ≥0 в точке его касания поверхности уровня Q_n+1 ={q∈R^m:Ψ(q)= Ψ(qⁿ⁺¹)}, причем сам луч 1n ортогонален к касательной поверхности уровня Q'_n в точке qⁿ.

Теоретические исследования и численные эксперименты показывают, что метод наискорейшего спуска для ряда кинематических схем роботов сходится медленно. Это связано с тем, что для многих манипуляционных роботов поверхности уровня функции обычно имеют так называемый овражий характер (2.21). Последнее означает, что по ряду переменных, образующих "склон оврага", даже небольшое изменение этих переменных приводит к резкому изменению значений функции, в то время как по остальным переменным, задающим "дно оврага", функция меняется незначительно.

Для ускорения сходимости иногда применяют метод Ньютона [28]. Если в градиентных методах при выборе направления убывания функции (2.21) используется лишь линейная часть ее разложения в ряд Тейлора, то в методе Ньютона используется квадратичная часть этого разложения. Возможность ускорения сходимости связана с тем, что квадратичная часть разложения аппроксимирует функцию гораздо точнее, чем линейная.

Метод Ньютона в задаче минимизации (2.21) имеет вид

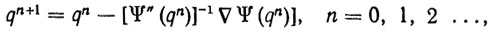(2.24)

где Ψ" - вторая производная функции Ψ по q.

Недостатком метода (2.24) является требование, чтобы начальное приближение q⁰ было достаточно близким к искомому решению q_* = arg min Ψ(q). При отсутствии хорошего начального приближения алгоритм (2.24) может расходиться, поэтому метод Ньютона целесообразно применять в сочетании с методом наискорейшего спуска, который призван предварительно отыскать приемлемое начальное приближение. Трудоемкость каждого шага у метода Ньютона, вообще говоря, выше, чем у градиентных методов. Тем не менее общий объем вычислений, необходимых для минимизации (2.21) с требуемой точностью при применении этого метода, может оказаться меньше, чем при применении более простых градиентных методов.

Описанные методы решения уравнения (2.1) требуют для своей реализации вычисления первых и даже вторых производных функций вида (2.21). Однако существуют и другие методы решения этой задачи, использующие лишь значения функции (2.21) и не требующие вычисления ее производных. К ним относятся метод покоординатного спуска и метод случайного поиска [28, 69].

В явном виде метод покоординатного спуска определяется алгоритмом [68]

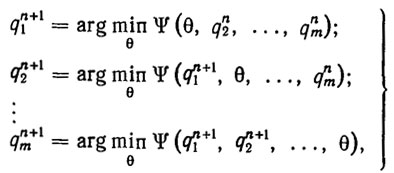(2.25)

где arg min Ψ (...,θ, ...) - такое значение θ, при котором Ψ имеет минимум по соответствующей переменной при фиксированных остальных. Обоснованием естественности алгоритма (2.25) для решения уравнения (2.1) являются некоторые особенности движения захвата манипулятора при изменении одной из его обобщенных координат: если меняется угловая координата, то захват движется по окружности; если меняется линейная координата, то захват движется по лучу. Эти соображения позволяют вычислить arg min Ψ в соотношениях (2.25) по элементарным формулам аналитической геометрии, что значительно упрощает реализацию метода покоординатного спуска.

Алгоритм (2.25) минимизирует функцию (2.21) с любой наперед заданной точностью δ. Скорость его сходимости слабо зависит от величины Ψ(q⁰), т. е. от выбора начального приближения q⁰. Другим достоинством алгоритма (2.25) является то, что он допускает свободный доступ к целенаправленному изменению обобщенных координат в процессе поиска решения. Это обстоятельство играет важную роль при автоматическом построении программных движений манипулятора с помощью алгоритма (2.25).

Наряду с описанными выше методами решения уравнения кинематики (2.1), существует большая группа алгоритмов поиска минимума функции (2.21), объединенных под названием метода случайного поиска. Этот метод характеризуется намеренным введением элемента случайности в алгоритм поиска, что увеличивает его гибкость. Многие алгоритмы метода случайного поиска можно представить в виде

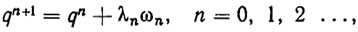(2.26)

где λn>0 - параметр; ωn - какая-либо реализация m-мерной случайной величины ω с известным законом распределения. В качестве координат ω_i случайного вектора со можно брать, например, независимые случайные величины, равномерно распределенные на отрезке [-1,1] [28].

Реализация алгоритма (2.26) предполагает наличие специального генератора случайных чисел, который формирует вектор со. Такие генераторы, называемые также датчиками случайных чисел, обычно оформляются в виде стандартных программ для ЭВМ. Если закон распределения случайного вектора ω не зависит от номера шага n, то алгоритм (2.26) не может "нащупать" направления быстрого убывания минимизируемой функции, поэтому он сходится медленно.

Для увеличения эффективности метода случайного поиска желательно, чтобы в алгоритме (2.26) целенаправленно изменялся закон распределения ω в зависимости от номера шага и от результатов предыдущих шагов. Такой поиск, обеспечивающий большую вероятность выбора перспективных направлений ωr убывания функции (2.21), называется случайным поиском с обучением. По мере обучения роль фактора случайности уменьшается и алгоритм (2.26) направляет поиск по "хорошим" направлениям убывания функции (2.21). В то же время элемент случайности позволяет алгоритму (2.26) быстро "адаптироваться" к резкому изменению свойств функции Ψ (q) в районе поиска.