
2.4. Метод кинематического синтеза программных траекторий
Рассмотренные алгоритмы решения обратной задачи о положении исполнительного механизма являются частью общей задачи гибкого программирования движений роботов. На кинематическом уровне эта задача формулируется так. Пусть для одной или нескольких выбранных точек на исполнительном механизме заданы уравнения кинематики вида (2.1). На обобщенные координаты наложены конструктивные ограничения (2.5) вида
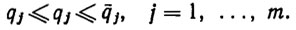 (2.27)
(2.27)
Они определяют в m-мерном эвклидовом пространстве Rm параллелепипед 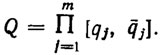 . Множество D=Ф(Q) является областью достижимости. Обозначим через М(q) множество в рабочем пространстве, занимаемое исполнительным механизмом в конфигурации q. Пусть Р - некоторые объекты, играющие роль препятствий. Введем следующую функцию - предикат препятствий:
. Множество D=Ф(Q) является областью достижимости. Обозначим через М(q) множество в рабочем пространстве, занимаемое исполнительным механизмом в конфигурации q. Пусть Р - некоторые объекты, играющие роль препятствий. Введем следующую функцию - предикат препятствий:
 (2.28)
(2.28)Пусть в области достижимости D задана траектория некоторого звена исполнительного механизма, причем расстояние между соседними точками достаточно мало. Для определенности будем считать, что задана траектория захвата манипулятора rk=0, 1, ..., Т. Программной траекторией (ПТ) механизма будем называть такую траекторию qkp, для которых при всех k= 0,1,…, T справедливы соотношения:
1)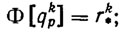 (2.29)
(2.29)
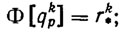 (2.29)
(2.29)2)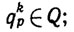 (2.30)
(2.30)
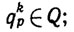 (2.30)
(2.30)3)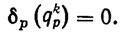 (2.31)
(2.31)
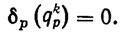 (2.31)
(2.31)
Описанные выше алгоритмы решения уравнения (2.1) индуцируют некоторый оператор А:
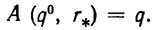 (2.32)
(2.32)
Функция А обладает тем свойством, что для любого начального приближения q0∈Q и любой целевой точки r*∈Q справедливо тождество Ф[A (q0,r*)] = r*. Кроме того, А[q0, Ф(q0)]=q0, поэтому оператор А можно назвать псевдообратным по отношению к. оператору Ф.
Оператор А позволяет записать следующую рекуррентную схему кинематического синтеза ПТ. Пусть даны траектории схвата rk* и начальная конфигурация q0 такая, что Ф (q0) = r0*. Дальнейшие элементы ПТ qkp определяются в силу рекуррентного алгоритма
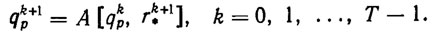 (2.33)
(2.33)Заметим, что вследствие псевдообратности оператора А справедливо Ф [qkp] = rk*.
Синтезируемая ПТ вида (2.33) должна обладать свойством непрерывности. В рассматриваемом дискретном случае это означает, что qkp должно удовлетворять требованию
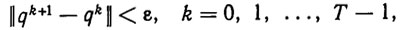 (2.34)
(2.34)где ε - малое положительное число. Необходимым условием выполнения (2.34) является малость величин ||rk+1 -rk* || (последнее предполагается).
При построении ПТ по методу (2.33) условие (2.34) будет выполнено, если оператор А удовлетворяет следующему свойству непрерывности: из малости ||r*-r0*|| следует малость ||q-q0||, где r0* = Ф (q0), q = A (q0, r). Поскольку A [q0, Ф (q0)] = q0, то для того чтобы оператор А обладал сформулированным свойством, нужна непрерывность А по r*. Однако для ряда промышленных роботов оператор А не является непрерывным по r*. Причиной этого является слишком широкая область задания оператора А, поэтому при построении ПТ приходится использовать лишь небольшую часть области задания А. Отметим, что метод построения ПТ в виде (2.33) достаточно общий. В качестве оператора А в нем может быть использовано отображение, индицируемое любым алгоритмом решения уравнения (2.1) по начальному приближению. В частности, здесь можно использовать оптимизационные алгоритмы вида (2.22)-(2.26).
На практике всегда имеются конструктивные ограничения (2.30), (2.31). Для их учета необходимо произвести следующую модификацию метода (2.33). Предполагая, что q0∈Ф, ПТ будем строить по формулам
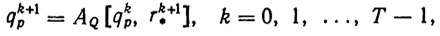 (2.35)
(2.35)где AQ - проекция А на множество Q. Заметим, что если А∈Q, то АQ=A. Теперь уже по построению qp (t) ∈ Q при всех t ∈ [0, Т].
Требование непрерывности, сформулированное выше по отношению к оператору А, в полной мере относится к оператору AQ. Что же касается свойства псевдообратности AQ, то здесь возникают некоторые осложнения. Дело в том, что это свойство зависит от множества Q и D. Оказывается [68], что необходимым условием псевдообратности оператора AQ является открытость отображения Ф : Q→ D. Более того, открытость отображения Ф необходима и достаточна для возможности построения непрерывного ПТ qkp для любой траектории схвата rk* из D. Однако это свойство для некоторых промышленных роботов не выполняется. В подобных случаях описанный метод кинематического синтеза ПТ должен дополняться процедурой предварительного планирования ПТ. Эта процедура, позволяющая автоматически удовлетворять конструктивным ограничениям (2.30) и требованию обхода препятствий (2.31), подробно описана в работах [42, 68].
|
ПОИСК:
|
© ROBOTICSLIB.RU, 2001-2019
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'