2.5. Скоростные алгоритмы программирования траекторий

Рассмотренные выше алгоритмы построения ПТ базируются на том или ином методе решения обратной задачи о положении, т. е. на решении уравнения кинематики (2.1), поэтому эти алгоритмы можно назвать позиционными. В отличие от них скоростные алгоритмы программирования движений основываются на управлении скоростью движений некоторых точек, фиксированных на отдельных звеньях механизма.

Для определенности рассмотрим методы и алгоритмы построения ПТ манипулятора, обеспечивающих желаемый закон изменения скорости движения избранных точек на его захвате. С этой целью продифференцируем по времени уравнение (2.1). Тогда получим следующее дифференциальное уравнение:

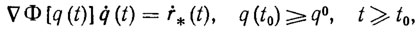(2.36)

где ṙ_* (t) - скорость движения выбранной точки на захвате; ΔФ (q) - матрица Якоби размерности З*m, зависящая от конфигурации q манипулятора. Введем 3*3 - матрицу-функцию

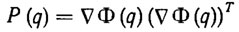(2.37)

и предположим, что она не вырождена. Тогда уравнение (2.36) можно записать в разрешенной относительно 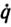форме

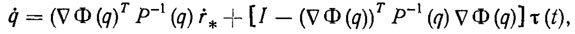(2.38)

где I - единичная m*m-матрица; τ (t) - пока произвольная вектор-функция размерности т.

Цель движения часто заключается в том, чтобы за заданное время Т = t_T - t₀ перевести манипулятор из заданной начальной конфигурации q₀ в желаемую конечную конфигурацию, удовлетворяющую соотношению

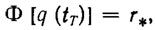(2.39)

где r_* - заданное целевое положение выбранной точки на захвате в области достижимости D. При этом искомая ПТ q_p (t) во все моменты времени t ∈ [t₀, t_r] должна удовлетворять конструктивным ограничениям (2.30) (т. е. q_p (t) не должна выйти за пределы множества Q в пространстве конфигураций), требованию обхода препятствий (2.31), а звенья манипулятора не должны самопересекаться.

Будем считать, что движение выбранной точки на захвате происходит с постоянной скоростью по прямой, соединяющей точки r_* (t₀) =Ф (q₀) и r_*, т. е.

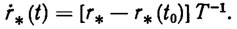(2.40)

Подставляя (2.40) в (2.38) и интегрируя полученное уравнение на промежутке [t₀,t_T], можно получить искомую ПТ q_p(t). Для этого следует задаться такой вектор-функцией τ (t), выбор которой, с одной стороны, не влияет на желаемый закон движения точки на захвате (2.40), а с другой - позволяет удовлетворить конструктивным ограничениям на обобщенные координаты, избежать столкновения манипулятора с препятствиями и самопересечения его звеньев. Эвристические соображения и формализованная процедура нахождения подходящей функции τ (t) как решения некоторой системы неравенств описаны в работе [5].

Поясним здесь основную идею выбора τ (t). Ограничения на ПТ q_p (t) можно записать в виде системы неравенств в пространстве конфигурации:

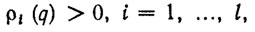(2.41)

где р_i (q) - некоторая функция, которую можно интерпретировать как расстояние манипулятора в конфигурации q, т. е. множества М (q), от множества "запрещенных конфигураций", определенного всеми заданными ограничениями. В частности, p_i (q) может означать расстояние от М(q) до внешних препятствий Р, тогда (2.41) определяет требование обхода препятствий.

Чтобы обеспечить выполнение неравенств (2.41) на ПТ q_p(t), воспользуемся следующим приемом [5]. Зададимся положительным числом ε. Если в некоторый момент времени t'>>t₀ нарушится i-e неравенство (2.41) при q=q_p(t), то выберем τ (t) в уравнениях (2.38) и (2.40) из условия

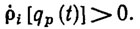(2.42)

Это условие гарантирует отход манипулятора от множества "запрещенных конфигураций".