2.6. Гибкие алгоритмы параметрического синтеза и оптимизации программных движений

Общим недостатком позиционных и скоростных алгоритмов программирования движений рабочих органов является то, что они строят ПТ с учетом лишь кинематических особенностей исполнительных механизмов роботов. При этом, по существу, игнорируются динамические ограничения, присущие как самим механизмам, так и связанным с ними приводам робота. В то же время учет динамических ограничений необходим с точки зрения принципиальной осуществимости и эффективности синтезируемых программных движений (ПД).

Рассмотрим метод и гибкие алгоритмы построения и оптимизации ПД с учетом динамики двигательной системы робота. Уравнения динамики исполнительных механизмов имеют вид, поэтому управляемые движения исполнительных механизмов однозначно определяются 2m-мерным вектором состояний

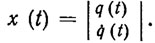
Среди множества возможных движений выберем ПДx = х_p(t), удовлетворяющее граничным условиям вида

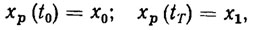(2.43)

где x₀x₁ - заданные начальное и конечное состояния рабочего органа. ПД х_p(t) должно удовлетворять при всех t∈ [t_Q, t_T] следующим конструктивным и динамическим ограничениям:

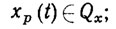
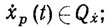
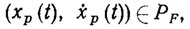(2.44) - (2.46)

где Q_x, Q_ẋ - некоторые заданные ограниченные области в пространстве конфигураций; P_F - подпространство управляемости [90, 107, 119], явный вид которого определяется уравнением динамики (2.2).

Следует также заметить, что ПД х_p(t) как частное решение уравнения динамики (2.2) при некотором допустимом управлении и = и_p(t) зависит от параметров ξ робота. В задачах программного управления предполагается, что эти параметры ξ [или их дрейф I (ξ)] известны. В следующей главе при синтезе адаптивного управления параметры ξ считаются неизвестными. В этом случае на класс ПД накладываются более жесткие ограничения, связанные с учетом структуры множества возможных значений параметров Q_ξ.

Построение ПД с учетом динамики робота сводится к решению двухточечной краевой задачи с граничными условиями (2.43) и ограничениями (2.44)-(2.46). Многие известные методы решения краевых задач здесь малоэффективны или даже непригодны. Трудности усугубляются высокой размерностью и нелинейностью уравнений динамики (2.2), а также сложным характером ограничений (2.44)-(2.46). Эффективным методом динамического синтеза ПД является метод параметризации ПД с учетом граничных условий (2.43), накладываемых на начальное и конечное состояния робота [107, ИЗ]. В этом методе воплощена идея априорного выполнения граничных условий (2.43) и учета структурного ограничения (2.46). Это достигается за счет специального выбора базисных функций. В таком подходе заложен глубокий смысл: при отыскании приемлемых параметров ПД уже не нужно заботиться об удовлетворении граничных условий (2.43) и динамического ограничения (2.46), так как они заранее учтены в конструкции базисных функций.

Рассмотрим подробнее один из вариантов метода параметризации ПД. Будем искать ПД в много параметрическом классе функций вида [107, 113]

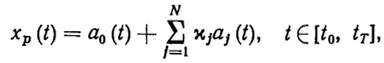(2.47)

где 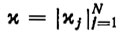- вектор искомых параметров; a₀(t), a₁(t),…, a_N(t)- заданные N-мерные вектор-функции. Эти функции будем называть базисными, если они удовлетворяют следующим условиям [113]:

1. функции 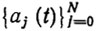таковы, что ПД (2.47) удовлетворяет граничным условиям (2.43) при любом выборе параметров х₁, ...,x_N
2. функции 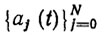и их производные 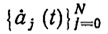попарно удовлетворяют структурному ограничению (a_j (t), ȧ_j(t)) ∈ P_F при всех t∈ [t₀,t_T]
3. функции 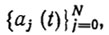взятые в любом конечном числе N, линейно независимы;
4. система аппроксимирующих функций, из которых выбираются базисные функции, полна в пространстве непрерывно дифференцируемых функций;
5. функции 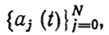достаточно просты с точки зрения их программной или аппаратной реализации.

Перечисленные требования к базисным функциям имеют следующий смысл. Первое требование обеспечивает и облегчает решение двухточечной краевой задачи, второе - гарантирует осуществимость параметризованного ПД (2.47) с учетом динамики робота, третье и четвертое - означают возможность экономного и вместе с тем сколь угодно точного представления ПД в виде (2.47) и, наконец, пятое обеспечивает простоту технической реализации искомого ПД. Заметим, что пренебрежение любым из этих требований может привести к грубым ошибкам или к неосуществимости параметризованного ПД.

Первая и важнейшая задача в рамках параметрического метода построения ПД заключается в рациональном выборе базисных функций. Рассмотрим некоторые примеры и общие рекомендации по конструированию базисных функций. Примером базисных функций, удовлетворяющих сформулированным требованиям, могут служить полиномы

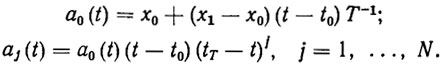(2.48)

В самом деле, при таком выборе базисных функций и при любых значениях параметров х₁, ..., x_N ПД (2.47) удовлетворяет граничным условиям (2.43) и динамическому ограничению (2.46), а также требованиям точной аппроксимации и простой реализации.

Другим примером рационального выбора базисных функций могут служить тригонометрические многочлены

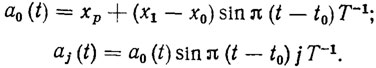(2.49)

Как видно из этих примеров, при конструировании базисных функций можно руководствоваться следующим правилом: в качестве функции а₀ (t) можно брать непрерывно дифференцируемую вектор-функцию, удовлетворяющую граничным условиям (2.34), а в качестве остальных базисных функций - функции вида

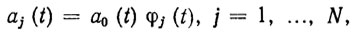(2.50)

где φ_j(t) - числовые функции из некоторой полной системы функции на [t₀; t_T], удовлетворяющие однородным граничным условиям, т. е.

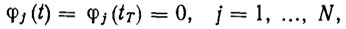
В качестве φ _j(t) можно брать рассмотренные выше полиномы и тригонометрические многочлены. Тем самым гарантируется возможность сколь угодно точной аппроксимации ПД в виде (2.47).

Значительный прикладной интерес представляет использование в качестве φ_j (t) "конечных элементов" [58], т. е. таких функций с конечным носителем, которые отличны от нуля только в небольшой (порядка шага сетки) окрестности интервала [t₀; t_T]. Простейшим примером могут служить кусочно-линейные функции вида [27, 69]

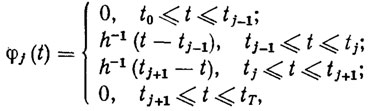(2.51)

где t₁ = t₀+h, t₂=t₀+2h,…, t_N=t₀+Nh=t_T - узлы сетки на [t₀, t_r] с шагом h. Эти функции обладают следующим свойством [69]: любую кусочно-линейную функцию с возможными изломами в узлах t_j можно представить в виде линейной комбинации 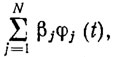, где в качестве коэффициентов Фурье стоят значения самой функции в точках t_j.

Большой интерес представляет также такая параметризация ПД, когда в качестве φ_j(t) берутся сплайны [28, 69, 85, 88, 127], т. е. кусочно-полиномиальные функции.

Конструирование базисных функций с учетом высказанных соображений обеспечивает соблюдение граничных условий (2.34) и динамического ограничения (2.46) при любом выборе параметров х₁,…, x_N ПД (2.47), а также приводит к высокой точности аппроксимации и простой реализации синтезируемых ПД. После того как базисные функции а₀(t), а₁ (t),…, a_N (t) выбраны, можно перейти к фактическому построению ПД.

Задача синтеза ПД сводится к отысканию приемлемых значений параметров х₁,…, x_n. Эти параметры должны определяться исходя из заданных ограничений (2.44) и (2.45). Заметим, что ограничения (2.44) и (2.45) на линейных ПД (2.47) превращаются в систему неравенств относительно параметров 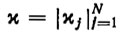. Таким образом, задача построения ПД в результате параметризации сводится к решению системы неравенств, описывающих ограничения (2.44) и (2.45) относительно параметров искомого ПД.

Для решения полученных неравенств можно применить известные методы нелинейного программирования [28]. Однако у роботов с большим числом степеней свободы, а также при сложном характере конструктивных ограничений использование этих методов наталкивается на принципиальные или вычислительные трудности. В подобных случаях более простым и эффективным может оказаться метод, использующий рекуррентные градиентные алгоритмы решения неравенств. Суть этого метода заключается в следующем [107]. Пусть для определенности множества Q_x и Q_ẋ представляют собой шары радиуса с_x и с_ẋ соответственно с центром в нуле. Тогда ограничения на ПД можно записать в виде следующей системы неравенств:

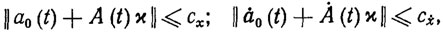(2.53)

где A (t) - n*N - матрица-функция, составленная из базисных функций а₁ (t),…, a_N (t);Ȧ (t) - производная А (t) по времени. Очевидно, что неравенства (2.52) и (2.53) выпуклы по х. Предположим, что эти неравенства разрешимы с некоторыми запасами δ₁>0 и δ₂> 0. Тогда существует вектор параметров х_* такой, что ПД (2.47) c_х = х_* удовлетворяет ограничениям (2.44) и (2.45) с соответствующими запасами. Заметим, что ввиду непрерывной дифференцируемости функций a_j (t), j= 1, ..., N матрицы-функции A (t) и Ȧ (t) равномерно ограничены, т. е. ||A(t)||≤с_A<∞,

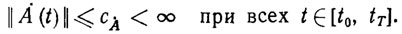(2.54)

В этих условиях для решения неравенств (2.52) и (2.53) применимы рекуррентные конечно-сходящиеся алгоритмы градиентного типа, предложенные в работах [132, 142]. Приведем явный вид одного такого алгоритма решения неравенств (2.52). Пусть x₀ - произвольное начальное приближение неизвестного вектора x_*. Зациклив систему неравенств (2.52) по t (с периодом Т), будем строить оценки x^k параметров ПД в соответствии с рекуррентным алгоритмом вида

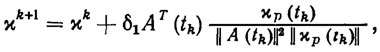(2.55)

где t_k - очередной момент нарушения неравенств (2.52) при х = x^k, t>t_k; х_p (t_k) - значение (2.47) при t = t_k, x =x^k.

С помощью метода функции Ляпунова легко показать, что алгоритм (2.55) является конечно-сходящимся, причем для числа его шагов справедлива оценка [132]

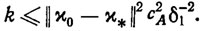(2.56)

Совершенно аналогично записывается рекуррентный конечно- сходящийся алгоритм решения неравенств (2.53), причем для числа его шагов справедлива оценка

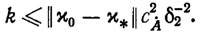(2.57)

Достоинством описанного параметрического метода построения ПД является простота и экономность представления ПД (2.47), а также гибкость, т. е. возможность быстрой перестройки ПД при изменении граничных условий или ограничений. Последнее обеспечивается тем, что структура блока синтезируемого ПД (2.47) задается с точностью до начального и конечного состояний х₀, х₁ и х . При этом изменение граничных условий влечет изменение базисных функций, а изменение ограничений порождает коррекцию параметров ПД без изменения его структуры.

Рассмотрим задачу оптимизации ПД. Эта задача имеет большое практическое значение, так как позволяет роботу экономить ресурсы и время в процессе выполнения рабочих операций. Выбор конкретного функционала качества вида (2.9) обычно возлагается на конструктора системы управления робота. После того как этот функционал выбран и зафиксирован критерий оптимальности (2.10), дело сводится к использованию методов теории оптимального управления.

Традиционные методы оптимизации, основанные на принципе максимума Л. С. Понтрягина [21, 58], сводят задачу к отысканию оптимального программного управления и⁰_p(t), после чего оптимальное ПД х⁰_p(t) получается как решение уравнения динамики при u=u⁰_p(t). При этом предполагается, что вектор параметров робота I известен. Однако решение этой задачи для роботов с большим числом степеней свободы наталкивается на значительные вычислительные трудности. Эти трудности усугубляются нелинейностью уравнений (2.2) и сложным характером ограничений на состоянии и управления.

Для преодоления указанных трудностей изменим формулировку задачи. Прежде всего заметим, что функционал (2.9), характеризующий качество ПД, не зависит явно от управления.

Поэтому задача оптимизации ПД может быть поставлена как следующая вариационная задача: построить ПД, оптимальное по отношению к функционалу качества (2.9), при соблюдении ограничений (2.44)-(2.46).

Сформулированная вариационная задача тесно связана с задачей оптимального программного управления. Однако она проще этой задачи в том отношении, что вместо дифференциальной связи здесь фигурирует значительно более простое динамическое ограничение (2.46). В процесс решения вариационной задачи оказывается возможным непосредственно строить оптимальное ПД (например, как решение уравнения Эйлера), не прибегая к трудоемкому предварительному поиску оптимального программного управления классическими методами. Следует отметить, однако, что и эта более простая задача далеко не тривиальна и достаточно трудоемка [особенно, если учесть ограничения (2.44) и (2.45), присущие всем промышленным роботам].

Значительный интерес представляют алгоритмические методы решения рассматриваемой задачи. Одним из таких методов является метод параметрической оптимизации ПД, предложенный в работах [107, ИЗ]. Этот метод основан на описанной выше параметризации ПД. Сущность метода заключается в том, что приближенное решение задачи оптимизации ПД ищется в виде (2.47). Подставляя параметризованное ПД в функционал (2.9), получим функцию

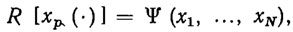(2.58)

зависящую от N параметров ПД.

Таким образом, задача оптимизации ПД свелась к следующей задаче нелинейного программирования: найти значения параметров искомого ПД вида (2.47) исходя из критерия оптимальности

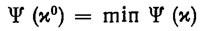(2.59)

и ограничений (2.44) и (2.45). Тем самым рассматриваемая вариационная задача редуцировалась к более простой задаче минимизации функции конечного числа переменных при ограничениях типа неравенств.