Глава 3. Адаптивное программное управление РТК

3.1. Цели и задачи адаптивного программного управления

Функциональные возможности и технико-экономические показатели РТК в значительной степени определяются тем, какие принципы и алгоритмы реализуются в их системе управления. Главным признаком, разделяющим РТК на поколения, служит именно принцип управления. Как уже отмечалось, в основе РТК первого поколения лежит принцип программного управления, а РТК второго и третьего поколений строятся на принципах адаптивного управления и искусственного интеллекта.

Рассмотрим основные цели, задачи и принципы управления РТК при различной степени информированности относительно динамических характеристик и условий эксплуатации. В рамках такого информационного подхода к управлению легко выявить недостатки программного управления и обосновать необходимость перехода к адаптивному управлению при функционировании РТК в не детерминированной производственной обстановке.

Для решения технологических задач, возложенных на РТК, необходимо обеспечить целенаправленные движения всех исполнительных механизмов с соблюдением требуемой ориентации рабочих органов и инструментов, диктуемые заданным технологическим процессом. Иными словами, нужно сначала по заданее запланированной последовательности технологических операций построить соответствующие программные движения (ПД) исполнительных механизмов РТК, а затем обеспечить такое управление этим ПД, чтобы переходные процессы удовлетворяли заданным требованиям по точности, быстродействию и т. п. Эти задачи решаются цифровыми и адаптивными системами программного управления.

Цифровые системы программного управления широко применяются в РТК первого поколения. Гибкость и целенаправленность управления в них достигается за счет предварительного программирования движений исполнительных механизмов. Методы и средства такого априорного программирования описаны в предыдущей главе. Поэтому ниже будем исходить из того, что требуемые ПД, обеспечивающие выполнение запланированных технологических операций, уже построены.

Задача управления ПД заключается в фактической обработке ПД с заданной точностью путем алгоритмического синтеза и программно-аппаратной реализации соответствующего закона управления РТК. В простейшем случае этот закон строится непосредственно по ПД как функция времени, поэтому в принципе для его реализации нужен только один датчик - таймер. При таком жестком программном управлении система управления РТК строится по разомкнутой схеме: в режиме программирования (обучения) в ее память вводится ПД; в рабочем режиме включаются приводы, реализующие программное управление. В этом заключается сущность принципа программного управления. Жесткий характер управления по этому принципу сильно ограничивает возможности РТК первого поколения.

Гораздо более совершенным является адаптивное программное управление РТК, основанное на принципах обратной связи и самонастройки закона управления ПД. Введение элементов адаптации поднимает цифровые системы программного управления на качественно новый, высший уровень, свойственный только человеку с присущими ему адаптационными возможностями.

Для формализованного описания методов программного и адаптивного управления введем в рассмотрение обобщенную динамическую модель РТК. Эта модель включает систему уравнений динамики, описывающих управляемые движения роботов и оборудования, входящего в состав РТК, а также систему конструкционных ограничений и внешний условий. В общем случае систему уравнений динамики РТК можно записать в виде векторного дифференциального уравнения

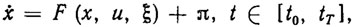(3.1)

где х = х (t) - n-мерный вектор состояний РТК; u=u (t) - m-мерный вектор управлений, подаваемых на приводы РТК; ξ=ξ (t) - р-мерный вектор параметров исполнительных механизмов и приводов; π=π(t) - n-мерный вектор внешних возмущений; t - текущее время; F - заданная n-мерная вектор-функция, зависящая от конструкционных особенностей РТК. Переменные х, u, π и параметры ξ имеют смысл реальных физических переменных и параметров, описывающих функционирование РТК. Так, например, в случае электромеханических РТК в число компонент вектора состояний х входят управляемые координаты исполнительных механизмов, токи в обмотках якорей приводов, а также их первые производные по времени; в число компонент вектора управлений - управляющие напряжения а, вырабатываемые системой управления РТК и подаваемые в цепи якорей приводов; в число компонент вектора параметров ξ - массо-инерционные характеристики звеньев исполнительных механизмов, заготовок, коэффициенты трения и упругости в редукторах, параметры двигателей.

Система дифференциальных уравнений (3.1) представляет собой аналитическую запись основных физических закономерностей, которым подчиняются управляемые движения роботов и технологического оборудования, образующих РТК. Чтобы принять систему уравнений (3.1) за обобщенную динамическую модель РТК, нужно охарактеризовать область определения функции F и конкретизировать класс постоянно действующих внешних возмущений π. Областью определения функции F, задающей структуру и свойства уравнений динамики (3.1), является совокупность возможных значений переменных х и u и параметров Границы этой области определены конструкционными ограничениями вида при всех t∈ [t₀,t_T]

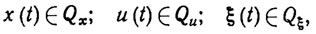(3.2)-(3.4)

где Q_x, Q_u,Q_ξ - заданные множества в пространстве состояний, управлений и параметров соответственно.

Внешние постоянно действующие возмущения я на практике всегда ограничены. Формально это означает, что

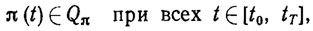(3.5)

где Q_π - область возможных значений внешних возмущений.

Допустимым управлением называется любой закон изменения управляющих воздействий u(t), удовлетворяющий ограничению (3.3). Управляемые движения РТК являются решением системы дифференциальных уравнений динамики (3.1) при заданном допустимом управлении. С формальной точки зрения реальное движение РТК описывается вектор-функцией х (t)= X (t, t₀, х₀, и, ξ, π), где х₀ - состояние РТК в начальный момент времени t₀. Если это движение удовлетворяет ограничению на состояния (3.2), то оно является допустимым.

Среди множества допустимых движений РТК выделим класс программных движений (ПД), т. е. множество таких допустимых движений х_p(t), которые обеспечивают выполнение требуемых технологических операций. При заданном ПД цель управления РТК обычно сводится к фактическому осуществлению ПД за счет синтеза соответствующего допустимого закона управления. Эффективные законы управления существенно зависят от структуры и свойств динамической модели РТК (3.1). В работах [107, 111, 119] установлено, что характерной чертой динамики широкого класса РТК является разрешимость системы уравнений относительно управления на некотором подмножестве

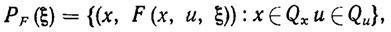(3.6)

называемом подпространством управляемости. Основываясь на этом важном свойстве, уравнения динамики (3.1) можно записать в более удобном (с точки зрения аналитического конструирования законов управления) виде, а именно:

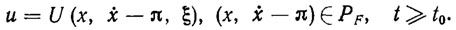(3.7)

Здесь U - оператор управления, определенный на множествах P_F и Q_ξ со значениями в Q_u и удовлетворяющий соотношению

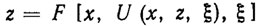
при всех (x, z) из P_F и всех ξ из Q_ξ.

Явный вид оператора управления U и подпространства управляемости P_F для конкретных типов роботов и технологического оборудования РТК будет приведен в последующих главах (см. также работы [107, 117, 119]).

Система ограничений (3.2)-(3.5) порождает ограничения на скорость изменения вектора состояний

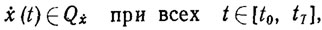(3.8)

где Q_ẋ - некоторое множество, определяемое по заданным множествам Q_x, Q_{u, Qξ , Qπ}, поэтому исходной системе ограничений -(3.5) можно поставить в соответствие эквивалентную ей систему, где вместо условия (3.3) фигурирует ограничение (3.8).

Новая система ограничений (3.2), (3.8), (3.4), (3.5) в сочетании с уравнением динамики РТК в разрешенной относительно управления форме (3.7) представляет собой обобщенную динамическую модель РТК. Эта модель играет важную роль не только при построении и оптимизации ПД РТК, но и при синтезе законов программного и адаптивного управления с учетом динамических особенностей РТК. Из свойств модели следует, что ПД х_p(t) должно удовлетворять ограничениям (3.2), (3.8).

Задача программного управления заключается в синтезе такого закона управления, который обеспечивает точное осуществление или стабилизацию заданного ПД х_p (t). Зная х_p(t), легко найти программное управление как функцию времени. Для этого нужно в управлении (3.1) положить π (t) = 0 и сделать подстановку х=х_p (t), ẋ =ẋ_p(t). В результате получим уравнение для определения программного управления u_p(t).

Чтобы найти программное управление в аналитическом виде, воспользуемся свойством разрешимости уравнения динамики

относительно управления на подпространстве. Тогда с учетом (3.7) получим следующую явную формулу для вычисления программного управления непосредственно по ПД:

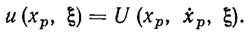(3.9)

Подставляя (3.9) в (2.66), убеждаемся, что совпадение реального движения х (t) и ПД х_p(t) возможно лишь при выполнении весьма жестких условий. Первое из этих условий - отсутствие неконтролируемых возмущений π(t). Второе условие заключается в совпадении х_p (t₀) с начальным состоянием х₀ РТК, т. е.

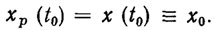(3.10)

Наконец, третье условие требует полной информации о дрейфе параметров ξ(t).

На практике строгое соблюдение указанных условий весьма затруднительно, а иногда и просто невозможно. Дело в том, что априорная информация о параметрах ξ (и тем более об их дрейфе) неполна и неточна. Кроме того, всегда имеются начальные возмущения е (t₀)=х₀-х_p(t₀) и неконтролируемые постоянно действующие возмущения π(t). Все это приводит к отклонению реального движения под действием жесткого программного управления (3.9) от ПД х_p(t). В этом проявляются принципиальные ограничения жесткого программного управления РТК.

Для обеспечения гибкости системы управления программное управление целесообразно сочетать с управлением по принципу обратной связи. В результате получим гибкие законы управления ПД с обратной связью. Главное преимущество таких комбинированных законов управления заключается в учете текущей информации о состоянии РТК с целью улучшения качества управления. Благодаря этому закон программного управления становится самокорректирующимся, а ПД устойчивым по отношению к начальным и постоянно действующим возмущениям.

Примером закона управления ПД с обратной связью по вектору состояний РТК может служить следующее управление [107, 112]:

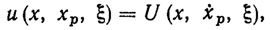(3.11)

которое в отличие от (3.9) обеспечивает устойчивость ПД х_p (t) на конечном интервале времени [t₀, t_T], Более эффективные законы управления, обеспечивающие асимптотическую устойчивость ПД, имеют вид [88, 107, 111]:

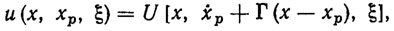(3.12)

где Г - некоторая устойчивая n*n-матрица коэффициентов усиления в каналах обратной связи. Специальным выбором структуры и элементов матрицы Г можно обеспечить заданный характер затухания переходных процессов е(t =x(t)-х_p(t) [107, 119].

Реализация гибких законов управления ПД вида (3.11) и (3.12) требует знания параметров ξ РТК. Однако на практике эти параметры обычно не только неизвестны, но и могут дрейфовать непредсказуемым образом в широком диапазоне, определяемом ограничением (3.4).

Внешние постоянно действующие возмущения π (t), существенно влияющие на точность отработки ПД, также неизвестны и не могут быть измерены датчиками информационной системы РТК. Априорные сведения о внешних возмущениях задаются ограничением (3.5).

Класс неопределенности условий функционирования РТК в целом определяется множествами Q_ξ и Q_π. Чем шире диапазон неконтролируемых изменений параметров ξ и возмущений π, тем шире класс неопределенности. Для многих РТК, работающих в составе ГАП, можно определить в явном виде класс неопределенности, характеризующий фактическую вариативность и не-детерминированность производственной обстановки.

В подобных нестационарных условиях с неопределенностью воспользоваться синтезированными законами программного управления, строго говоря, нельзя. Если все же использовать эти законы, предварительно заменив в них неизвестные параметры ξ некоторыми правдополобными оценками τ, то в замкнутой двигательной системе РТК возникнут неконтролируемые параметрические возмущения. Действие этих возмущений (в сочетании с начальными и постоянно действующими внешними возмущениями) может привести к нежелательным динамическим эффектам - снижению точности отработки ПД, автоколебаниям или неустойчивости.

Новый подход к управлению РТК в условиях неопределенности базируется на принципе адаптации системы управления к за ранее неизвестным меняющимся свойствам РТК и окружающей его производственной обстановки. В процессе адаптации происходит самонастройка и приспособление системы управления к фактической обстановке. Реально это проявляется в изменении структуры и параметров системы управления так, чтобы гарантировать осуществление ПД при соблюдении конструктивных ограничений в нестационарных и неопределенных условиях эксплуатации РТК.

Характерной чертой адаптивных систем управления является то, что недостаток априорной информации и неконтролируемый дрейф параметров компенсируется в них надлежащей обработкой сенсорной информации, поступающей от информационной системы РТК. Для обработки этой информации служат алгоритмы адаптации, осуществляющие самонастройку параметров закона управления, а также коррекцию ПД.

Наличие развитых средств очувствления и связанных с ними алгоритмов адаптации принципиально отличает адаптивные системы управления РТК от систем программного управления, описанных в предыдущей главе. Благодаря этим средствам и алгоритмам осуществляется автоматическое приспособление РТК к не детерминированным и изменяющимся условиям эксплуатации.

Адаптивная постановка задач управления ПД в отличие от классической предполагает, что конструктору неизвестны параметры ξ динамической модели РТК и постоянно действующие возмущения π. Вследствие этого законы управления с обратной связью (3.11) и (3.12) нуждаются в доопределении: должны быть указаны алгоритмы поиска приемлемых оценок τ неизвестных параметров ξ, использующие обратную связь от датчиков информационной системы РТК. Если эти алгоритмы обеспечивают осуществление ПД с требуемой точностью для любых возможных значений параметров ξ ∈Q_ξ и возмущений π ∈ Q_π, то будем называть их алгоритмами адаптации. Соответствующие законы управления с автоматической адаптацией (самонастройкой) параметров τ будет называть адаптивными в заданном классе неопределенности {Q_ξ,Q_π}

Задача адаптации заключается в синтезе алгоритмом адаптации с требуемыми свойствами. Решение этой задачи тесно связано с контролем качества управления. Введем функцию качества вида Ф (τ, t)=Ф[u(ξ), х(t), τ], значения Ф которой могут быть измерены или вычислены в любой момент времени t. Это требование необходимо для реализуемости алгоритмов адаптации. Цель адаптации удобно задавать в форме неравенств, связывающих управления u, состояния х и оценки т. В качестве таких неравенств можно взять систему неравенств вида:

(3.13)

Эти неравенства должны конструироваться таким образом, чтобы их выполнение обеспечивало требуемую близость реального движения РТК и ПД. Неравенства, обладающие указанными свойствами, будем называть эстиматорными.

Решение задачи адаптации сводится к синтезу алгоритмов решения эстиматорных неравенств (3.13). Смысл этих алгоритмов заключается в формировании приемлемых оценок τ неизвестных параметров ξ, причем, если неравенства (3.13) нарушаются при некотором τ= τ (t), то это свидетельствует о неудовлетворительности текущей оценки τ(t) и о необходимости ее скорректировать. Если же неравенства (3.13) выполнены, то это говорит о приемлемости как самих оценок, так и синтезированного на их основе адаптивного закона управления. Таким образом, алгоритм решения эстиматорных неравенств выступает как алгоритм адаптации. Отсюда ясна важная роль и значение эстиматорных неравенств.

Характерной чертой неравенств (3.13) является то, что в каждый момент времени t известно лишь текущее значение функции φ (τ,t), но не будущие ее значения. Последние зависят от будущего выбора оценок и управляющих воздействий, поэтому алгоритм адаптации должен находить решение заранее не заданных эстиматорных неравенств.

Большинство алгоритмов адаптации можно разбить на два класса:

1. непрерывные алгоритмы, когда оценка τ(t) определяется как решение дифференциального уравнения адаптации;
2. дискретные алгоритмы, когда оценка τ(t) =τ (t_k) определяется в дискретные моменты времени t_k, k= 0, 1,…, по рекуррентным формулам.

Общая схема непрерывных алгоритмов такова: оценка τ(t) определяется как решение дифференциального уравнения адаптации вида

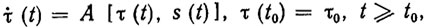(3.14)

где s(t) - текущая информация; τ₀ - произвольная начальная оценка из множества Q_ξ; А - оператор адаптации (он таков, что оценки τ (t) сходятся к идеальному решению ξ или в некоторую его окрестность).

Дискретные алгоритмы адаптации описываются следующей системой соотношений:

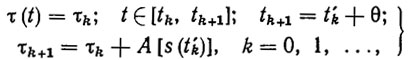(3.15)

где τ₀ - произвольная начальная оценка; t'_k - первый момент нарушения эстиматорных неравенств (3.13) при τ= τ_k, t≥t_k; θ- время, необходимое для вычисления новой оценки τ_к+1 в соответствии с алгоритмом (3.15) по имеющейся к моменту t'_k информации s(t'_k); А - оператор адаптации.

Таким образом, решение задачи адаптации сводится к конструированию непрерывных иди дискретных алгоритмов адаптации вида (3.14) или (3.15), которые генерируют траекторию τ(t), t≥t₀ или последовательность оценок τsub>k, k=0,1,…, сходящуюся к некоторому решению эстиматорных неравенств (3.13).

Важнейшими требованиями, предъявляемыми к алгоритмам адаптации, являются:

1. конечная сходимость, т. е. конечность общего времени нарушения эстиматорных неравенств на траектории алгоритма адаптации;
2. помехоустойчивость, т. е. устойчивость алгоритма адаптации по отношению к вычислительным погрешностям;
3. простота и реализуемость алгоритма адаптации;
4. оптимальность, т. е. выбор оператора адаптации (или его параметров) из некоторого условия оптимальности.

Цель адаптивного управления зависит от режима эксплуатации РТК. Анализ технологической задачи с позиций теории управления позволяет выделить следующие типовые режимы: стабилизация ПД, терминальное управление и самонаведение.

Цель управления в режиме стабилизации заключается в отслеживании ПД с заданной точностью ε сразу или по прошествии некоторого времени переходного процесса Т_p≡t_p-t₀, т. е.

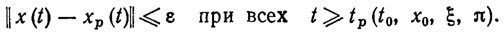(3.16)

Цель терминального управления заключается в переводе РТК из начального состояния х₀ в желаемое конечное состояние х₁ за заданное время Т≡ t_T-t₀, т. е.

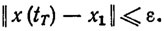(3.17)

Наконец, цель самонаведения имеет вид (3.17) с той разницей, что траектория и время наведения здесь заранее не фиксируются.

Для выполнения сформулированных целевых условий необходимо синтезировать закон управления u=u(t, х, τ) с обратной связью по вектору состояний х и с самонастройкой параметров τ. Этот закон, естественно, не должен зависеть от неизвестных параметров ξ ∈Q_ξ и возмущений π ∈ Q_π. Если синтезированный закон управления и алгоритм адаптации обеспечивают достижение цели управления для любых значений ξ и π из класса неопределенности {Q_ξ,Q_π}, то реализующую их систему управления РТК будем называть адаптивной в классе {Q_ξ, Q_π}. При синтезе и расчете адаптивных законов управления его структура и параметры должны быть выбраны так, чтобы гарантировать выполнение конструктивных ограничений на состояния и управления на всем рассматриваемом интервале движения.

Раскроем смысл и особенности приведенных выше формализованных целевых условий и режимов в частных задачах адаптивного программного управления роботами и технологическим оборудованием, входящими в состав РТК. При этом общая задача адаптивного управления РТК расщепляется на ряд локальных задач и целей управления. Применительно к промышленным манипуляционным роботам целевое условие (3.16) обычно соответствует режиму контурного управления, а целевое условие (3.17) - режиму позиционного управления. Часто оба эти режима реализуются в одной адаптивной системе программного управления.

Для координатно-измерительных роботов цель управления заключается в самонаведении измерительного щупа или обходе детали по контуру, который заранее не задается и зависит от формы и размеров измеряемой детали. В последнем случае речь идет, по существу, об отслеживании некоторого ПД, которое заранее неизвестно.

Целью адаптивного управления транспортными роботами обычно является либо отслеживание заданного ПД, соответствующего маршруту безопасного движения робота в реальных условиях производства, либо приведение робота в заданное состояние, соответствующее, например, его остановке в определенной точке с заданной ориентацией. При этом траектория и время приведения могут задаваться заранее (что соответствует режиму терминального управления) или определяются в процессе управления (что соответствует режиму самонаведения).

Целевые условия при адаптивном программном управлении станками часто имеют вид (3.16) и (3.17). Это соответствует так называемому контурному и позиционному управлению станками.

При координатном управлении перемещением детали или инструмента по принципу "от точки к точке" главным является точное позиционирование, а вид траектории, по которой происходит самонаведение, не имеет существенного значения и влияет только на время обработки соответствующей технологической операции, т. е. на производительность станка. Адаптивное координатное управление применяется в сверлильных и координатнорасточных станках, в автоматах для точечной сварки и т. п. Для него характерен дискретный характер программы движения: после перемещения детали или инструмента в положение с заданными координатами и фиксации в нем выполняется соответствующая технологическая операция (например, сверление или развертывание отверстия, пайка и т. п.).

Контурное адаптивное управление применяется в основном в токарных и фрезерных станках всех видов, а также в технологическом оборудовании с непрерывным перемещением рабочих органов. При этом ПД обычно строится в абсолютных координатах непосредственно по чертежу детали или по его "образу", хранящемуся в автоматизированном банке данных. Часто контур детали состоит из отрезков прямых и дуг окружностей. В подобных случаях применяются комбинированные позиционно-контурные адаптивные системы управления. В простейшей задаче обточки валов на токарных станках, когда ПД представляет собой ступенчатую функцию, целью управления является отработка этого ПД путем поочередного включения и регулирования то продольной, то поперечной подачи.