7.3. Язык предикатов и адаптивный поиск логического вывода

Для организации осмысленного диалога между человеком и ЭВМ и автоматизации решения интеллектуальных задач в процессе управления РТК необходим специальный язык. Этот язык должен быть удобным средством формулировки заданий, представления знаний, поиска планов и принятия решений. Он должен также предоставить системе управления РТК с элементами искусственного интеллекта необходимую основу для логических умозаключений. Благодаря способности рассуждать на своем внутреннем языке формул система управления РТК сможет решать многие интеллектуальные задачи на уровне здравого смысла.

Исчисление предикатов является простейшим логическим языком, удовлетворяющим указанным требованиям. На этом формальном языке можно записать многие предложения и утверждения естественного языка, что позволит формализовать знания. В исчислении предикатов содержатся также процедуры (правила) поиска логического вывода. Это позволит придать ЭВМ способность логически рассуждать и строить умозаключения, необходимые для понимания смысла задания и решения возникающих интеллектуальных задач. Важно отметить, что исчисление предикатов и реализующий его логический язык программирования "Пролог" будут использоваться в интеллектуальных ЭВМ пятого поколения.

Исчисление предикатов содержит следующий экономный алфавит символов [108, 133]:

1. Предметная область и термы. Объекты и понятия, которыми приходится оперировать при решении той или иной интеллектуальной задачи, относятся к некоторому множеству Ω, называемому предметной областью. Фиксированные элементы этой области называются предметными постоянными (константами). Переменные, принимающие значения из Ω, называются предметными переменными. Предметные переменные, константы, а также функции от них называются термами.
2. Переменные высказывания и предикаты. Переменные, принимающие значения "истина" (И) или "ложь" (Л), называются переменными высказываниями. Функции, аргументы которых принимают значения из области Ω, а сами функции принимают всего лишь два значения (И или Л), называются предикатами. Предикат, аргументами которого являются n предметных переменных, называется -местным. Если n= 1, то предикат обычно определяет некоторое свойство предмета, если n≥2, то предикат может выражать n-арное отношение между предметами.
3. Элементарные (атомарные) формулы. Высказывания и выражения вида А(ω), F (b,c), где A, F - предикаты, а ω, b, c - предметные переменные или константы, называются элементарными, или атомарными, формулами. Эти формулы (как высказывания, так и предикаты) всегда принимают лишь два значения: истинно или ложно, поэтому их можно связывать с помощью логических операций, образуя новые формулы.
4. Логические операции. К числу логических операций относятся конъюнкция & ("и"), дизъюнкция ∨ ("или", "и/или"), отрицание 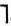("не", "неверно, что ..."), импликация → ("если то ...", "влечет"), эквивалентность ↔ ("эквивалентно", "тогда и только тогда"). Эти операции определяются следующим образом: А → В истинно тогда и только тогда, когда А и В имеют одинаковые значения; А→В ложно тогда и только тогда, когда А истинно, а В ложно; А & В истинно тогда и только тогда, когда А и В истинны; А ∨В ложно тогда и только тогда, когда и A, и В ложны; 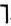A истинно тогда и только тогда, когда А ложно.
5. Скобки и кванторы. Кроме пяти упомянутых логических связок, в исчислении предикатов употребляются еще скобки ( ) и две новые операции ∀, ∃ выражающие собой утверждения всеобщности и существования. Символ ∀ называется квантором всеобщности, а символ ∃ - квантором существования.

Пусть Р (ω) - предикат, определенный для каждого элемента со некоторой области Ω. Тогда выражение ∀ωР(ω) истинно, когда Р(ω) истинно для каждого элемента ω области Ω, и ложно - в противном случае. Это высказывание уже не зависит от ω. Ему соответствует словесное выражение "для всякого ω Р (ω) истинно".

Высказывание ∃ωP(ω) истинно, если существует элемент ω области Ω, для которого Р (ω) истинно, и ложно - в противном случае. В обычном языке этой формуле соответствует выражение "существует ω такое, что Р (ω) истинно".

Каждая формула в исчислении предикатов является некоторой конечной последовательностью символов из указанного выше алфавита, составленной по следующим правилам.

Пусть формула А содержит свободную переменную ω, т. е. переменную, не связанную кванторами ∀ или ∃. Тогда выражения

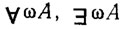(7.1)

также являются формулами. В этих формулах ω - это уже связанная переменная. Остальные же предметные переменные, которые были свободными в A, остаются свободными и в новых формулах (7.1).

Пусть теперь A и В - такие формулы, что в них нет предметных переменных, которые связаны в одной формуле и свободны в другой. Тогда выражения

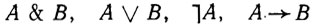(7.2)

являются формулами. Таким образом, правильно построенной формулой, или, короче, формулой исчисления предикатов, называется конечная последовательность из символов, которая строится на базе элементарных (атомарных) формул путем перехода от формулы A к формулам (7.1) и от формул A и В к формулам (7.2). Если в формуле A сделать замену переменных (как свободных, так и связанных), то полученное выражение снова будет формулой.

Элементарная формула или ее отрицание, входящие в правильно построенную формулу, называются литерами, а дизъюнкция литер называется простым дизъюнктом. Если дизъюнкт не содержит никаких литер, то он называется пустым дизъюнктом и обозначается nil.

Язык логики предикатов содержит в себе всю алгебру высказываний, т. е. элементарные высказывания, принимающие значения "истинно" или "ложно", логические операции и, следовательно, все мыслимые формулы. Кроме того, этот язык допускает переменные высказывания, отнесенные к произвольной предметной области. Благодаря этому формулам языка можно дать ту или иную интерпретацию, т. е. с содержательной (семантической) точки зрения формулы можно сделать осмысленными. Приведем строгое определение интерпретации и некоторых связанных с ней понятий.

Чтобы определить интерпретацию, необходимо прежде всего указать предметную область Ω, которая выступает как своеобразный "носитель" языка. Тогда интерпретация I произвольной формулы А включает в себя предметную область Ω и значения всех констант, функциональных и предикатных, встречающихся в Ω. Таким образом, интерпретация - это предписание, противопоставляющее языковым символам формулы некоторые "настоящие" объекты предметной области Ω, а именно: константам - элементы Ω, функциональным символам - конкретные функции, предикатным символам - конкретные предикаты. Образно говоря, интерпретация наполняет содержанием (смыслом) формулы исчисления предикатов.

При заданной интерпретации всякая формула (не содержащая свободных переменных) представляет собой высказывание, которое истинно или ложно. Если при данной интерпретации I каждая из формул А₁,..., А_m принимает значение истинно, то будем говорить, что интерпретация I удовлетворяет системе формул 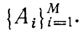. Формула В выводима (логически следует) из некоторой системы формул 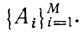если каждая интерпретация I, удовлетворяющая этой системе, удовлетворяет также и В. Заметим, что если некоторая интерпретация удовлетворяет заданной системе формул, то она удовлетворяет и любой формуле, выводимой из этой системы. Методы доказательства того, что некоторая формула В_M выводима (логически следует) из заданной системы формул 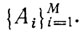, когда это на самом деле так, играют важную роль при логическом анализе и решении интеллектуальных задач. Остановимся на этом подробнее.

Предположим, что формула В выводима из системы 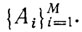. Тогда любая интерпретация, удовлетворяющая 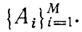удовлетворяет В, но не удовлетворяет 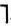В. Следовательно, никакая интерпретация не удовлетворяет объединению 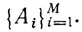. Если некоторая система формул не удовлетворяется ни при какой интерпретации, то она называется противоречивой. Так, если В выводима из 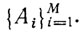, то формула 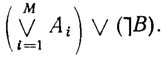противоречива. И, наоборот, если 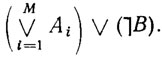противоречива, то B должна логически следовать из системы 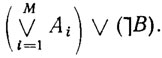. Именно эта концепция выводимости лежит в основе поиска логического вывода в исчислении предикатов.

Одним из наиболее удобных средств поиска логического вывода является так называемый метод резолюций [133]. В основе этого метода лежит идея доказательства от противного. Она заключается в том, что вместо заданной формулы В, которая предполагается тождественно истинной, рассматривается ее отрицание 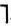B и доказывается противоречивость (не удовлетворимость) этой формулы. Процесс поиска логического вывода завершается, как только устанавливается справедливость некоторых альтернативных формул L и 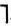L. Полученное противоречие доказывает не удовлетворимость формулы 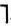B и, следовательно, тождественную истинность исходной формулы В.

При использовании метода резолюций формула 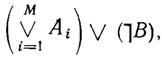, противоречивость которой доказывается, предварительно представляется в конъюнктивной нормальной форме, т. е. в виде

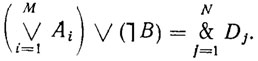(7.3)

Принцип резолюции в исчислений высказываний состоит в выборе двух дизъюнктов D_i и D_j, в один из которых входит литера L, а в другой - ее отрицание 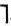L.Резольвентой называется новая формула R=Р ∨ Q получаемая из D_i=Р ∨L и D_j=Q ∨(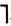L)путем вычеркивания литер L и 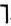L. Это соответствует применению правила "модус поненс" к рассматриваемым дизъюнктам.

В исчислении предикатов принцип резолюций усложняется. В этом случае дизъюнкты, вообще говоря, зависят от переменных. Пусть, например, D_i=Р(ω)∨L(ω), D_j=Q (ω) ∨( 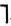L φ(ω)). Теперь уже нельзя вычеркнуть литеры L(ω) и 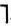L (φ(ω)), так как они зависят от разных переменных. Поэтому приходится подставлять вместо этих переменных подходящие термы. Так, подставляя в D_i вместо ω терм τ=φ(ω), получим D_i=Р(φ(ω)) ∨L (φ (ω)). Отсюда находим резольвенту R=Р(φ(ω)) ∨Q(ω). Получение очередной резольвенты в форме пустого дизъюнкта nil свидетельствует о том, что доказываемая формула В действительно логически следует из заданной системы формул .

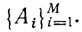Число резольвент, формируемых в процессе поиска логического вывода, конечно. Оно существенно зависит от выбора стратегии поиска, т. е. правила выбора дизъюнктов для синтеза очередной резольвенты. Большой практический интерес представляет оптимальная стратегия, позволяющая получить решение за минимальное число шагов. Синтез такой стратегии, связанный с нахождением кратчайшего пути на графе, наталкивается на значительные трудности. Поэтому разработано много эвристических стратегий, позволяющих сокращать число резольвент, необходимых для решения задачи. Например, при наличии в формуле (7.3) одночленных дизъюнктов целесообразно строить резольвенты именно с них (стратегия предпочтения одночленов [133]). Весьма эффективными могут быть также разного рода семантические и адаптивные стратегии [108, 133].

В некоторых интеллектуальных задачах факт выводимости заданной формулы В (трактуемой как задание или вопрос) из системы формул (трактуемых как аксиоматическое описание знаний и накопленного опыта) оказывается недостаточным. Примером может служить задача планирования поведения робота. В подобного рода задачах нужно знать тот ответный терм m, при котором данная формула В(ω) логически выводима из системы аксиом {А_i(ω)}^M_i=1. Иными словами, нужно выяснить, следует ли логически формула ≓ωВ(ω) из заданной системы аксиом и, если следует, то при каком значении переменной ω=τ это достигается.

Заметим, что именно умение отыскивать такие значения (ответный терм) для переменной, связанной квантором существования, позволяет ставить роботу вопросы весьма общего характера и осуществлять диалог с ним. Например, если спросить у робота: "Какие действия и в какой последовательности нужно совершить, чтобы собрать из имеющихся деталей определенную конструкцию?", то ответом на этот вопрос должна быть не просто констатация факта, что сборка данной конструкции возможна; робот должен предложить еще и развернутый план (технологический маршрут) сборки.

Методы извлечения ответного терма в процессе поиска логического вывода хорошо известны [133].

Описанные язык исчисления предикатов и методы поиска логического вывода представляют собой эффективное средство для автоматического решения широкого класса интеллектуальных задач. Этот логический язык, а также связанный с ним метод резолюций позволяют ЭВМ логически рассуждать и самообучаться. Остановимся на этом подробнее.

Первым этапом автоматического решения задач, требующих логического анализа, является формулировка этих задач в терминах исчисления предикатов. Для этого нужно прежде всего задать предметную область, т. е. совокупность относящихся к решаемой задаче объектов, и выделить их существенные свойства. Далее нужно, присвоив определенный содержательный (семантический) смысл предикатным и функциональным символам, формализовать данные и условия задачи в виде правильно построенных формул, удовлетворяющих рассматриваемой интерпретации. Эти формулы, описывающие условия задачи, называются аксиомами.

Аксиомы можно рассматривать как концептуальное определение совокупности рассматриваемых объектов, их свойств и отношений между ними.

Формулировка задачи на языке исчисления предикатов - это один из наиболее ответственных этапов интеллектуального программирования. На этом этапе от человека требуются глубокие знания существа решаемой задачи. Практически весьма важно, чтобы формулировка задачи (связанная с заданием системы аксиом и формулы цели) была, по возможности, простой, не "засоренной" второстепенными данными.

Эффективность поиска логического вывода можно увеличить путем уменьшения числа предикатов и аксиом, определяющих данные и условия задачи. С этой целью разумно использовать ранее доказанные формулы или ввести более сложные предикаты, образующие новые аксиомы, которые можно рассматривать как результат обучения в процессе решения задачи. Такие аксиомы, описывающие на языке исчисления предикатов приобретаемый опыт, можно назвать аксиомами обучения. Введение аксиом обучения позволяет увеличивать и улучшать знания о рассматриваемом классе задач в процессе их непосредственного решения. Таким образом, аксиомы обучения являются по существу средством представления новых знаний и уточнения старых.

При интеллектуальном программировании важную роль играют стратегии поиска логического вывода. Именно стратегия определяет, в каком порядке будут образовываться резольвенты и, следовательно, насколько быстро будет найдено решение задачи. Образно говоря, стратегия - это та активная часть, способная к обучению и адаптации, которая определяет машинный способ рассуждений в процессе решения задач. Она как бы подсказывает ЭВМ идею поиска логического вывода исходя из заданной системы аксиом, в которой заключены необходимые для решения задачи знания. Если идея (стратегия) хороша, то решение будет найдено быстро. Весьма важно также, чтобы в системе аксиом были достаточно полно отражены не только необходимые сведения об условиях задачи, но и прошлый опыт решения задач. Поскольку хорошие идеи (стратегии) часто имеют своим источником прошлый опыт и ранее приобретенные знания, то это наводит на мысль о целесообразности синтеза и использования адаптивных стратегий.

Стратегию поиска логического вывода будем называть адаптивной, если она целенаправленно меняется (подстраивается) в процессе решения задач в зависимости от приобретаемого опыта [108]. Примерами простейших адаптивных стратегий могут служить семантические стратегии, в которых сначала выбираются термы, соответствующие наиболее интересным объектам, затем - предикаты, описывающие их свойства, и, наконец, формулы, содержащие эти свойства.

При синтезе адаптивных стратегий важную роль играет критерий предпочтения аксиом обучения (хранящихся в памяти ЭВМ наряду с исходной системой аксиом), который позволяет уменьшить исходную неопределенность относительно условий решения задачи. Использование аксиом обучения особенно эффективно в тех случаях, когда в них либо раскрывается неопределенность (т. е. содержится новая необходимая для решения задачи информация), либо запоминается в компактной форме часто встречающийся в рассматриваемом классе задач фрагмент решения. В самом деле, если в процессе решения очередной задачи потребуется вывести уже доказанную ранее формулу, то критерий предпочтения аксиом обучения сократит общее число шагов поиска логического вывода по крайней мере на длину вывода соответствующей аксиомы обучения.

Рассмотрим теперь применение языка исчисления предикатов и связанных с ним средств поиска логического вывода для автоматического формирования понятий, представления знаний, синтеза решающих правил, распознавания объектов и анализа сцен. Решение этих задач позволит создать соответствующие элементы интеллекта РТК.