7.4. Автоматическое формирование понятий и аксиоматическое представление знаний

Проблема формирования понятий и представления знаний играет важную роль не только при организации интеллектуального интерфейса, но и при разработке адаптивных систем распознавания для РТК. Острая необходимость в эффективных методах решения этой проблемы возникает, например, при распознавании речевых команд, при анализе видеосцен и при моделировании окружающей среды в памяти управляющей системы РТК.

Для формирования понятий и представления знаний, связанных с задачей распознавания, воспользуемся описанным выше языком исчисления предикатов. Роль предметной области Ω здесь играет множество объектов из М классов. Каждому классу объектов Ω_k , k=1, ..., М, соответствует свой решающий предикат вида

(7.4)

представляющий собой характеристическую функцию класса Ω_k.

На практике классы Ω₁, … , Ω_M не заданы, поэтому и решающие предикаты (5,6) неизвестны.

Предположим, что информационная система РТК позволяет ему определять некоторые свойства объектов, подлежащих распознаванию. Каждому такому свойству поставим в соответствие предикат-признак вида

(7.5)

Предикаты ξ_i(ω), i=1,… ,n характеризуют локальные или глобальные свойства объектов, которые непосредственно воспринимаются РТК. В терминах этих предикатов-признаков каждому фиксированному объекту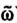
можно поставить в соответствие его логическое описание z(ω) - элементарную конъюнкцию всех предикатов вида (7.5), зарегистрированных на данном объекте.

В режиме обучения РТК предъявляются типичные образцы объектов из разных классов. Например, в случае сборочного РТК предъявляются детали, из которых нужно собрать изделие. При этом "учитель", в роли которого обычно выступает человек, сообщает РТК, к какому классу каждый данный объект принадлежит. Подмножество предъявленных "эталонных" объектов Ω ₀ называется обучающей выборкой. По обучающей выборке легко построить логическое описание (ω) всех эталонных объектов. Дизъюнкцию таких описаний объектов из одного и того же класса назовем аксиомой этого класса и обозначим

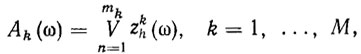(7.6)

где m_k - число эталонных объектов k-то класса, содержащихся в обучающей выборке Ω,sub>0.

Аксиома класса (7.6) задает логическое описание класса Ω_k в терминах исходных предикатов-признаков. Процесс построения аксиом классов (по мере предъявления РТК эталонных объектов) по сути представляет собой процесс формирования понятий РТК об объектах окружающей среды. В идеальном случае аксиомы классов должны обладать следующим свойством:

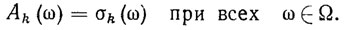(7.7)

Однако на практике ввиду ограниченности обучающей выборки построить такую идеальную систему аксиом вида (7.6) обычно не удается. Поэтому в принципе возможны ошибки при распознавании объектов, не входящих в обучающую выборку.

Для оценки качества системы аксиом классов введем понятие экстраполирующей силы. Именно экстраполирующей силой системы аксиом классов вида (5.8) на множестве Ω будем называть величину

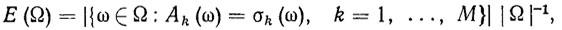(7.8)

где |Ω| - мощность (число, элементов) множества Ω.

Обычно качество системы аксиом классов оценивается либо на обучающей выборке Ω₀, либо на контрольной выборке, если таковая имеется. Чем больше E, тем лучше сконструированная система аксиом, т. е. тем большую информацию о классах она несет.

Благодаря обучению понятиям РТК приобретает способность к решению задач распознавания. Среди них наиболее важными в прикладном отношении являются такие задачи, как классификация речевых команд или идентификация дикторов, распознавания обычных яркостных или дальностных (т. е. полученных с помощью дальномера) изображений отдельных объектов и рабочих сцен, находящихся в поле зрения РТК.

Характерной особенностью ряда задач такого рода является то, что классы распознаваемых объектов инвариантны относительно той или иной группы преобразований G. Формально это означает, что значения решающих предикатов (7.4) не изменяются при всевозможных преобразованиях g из G, т. е. kσ_k(ω)=σ(gω) при всех g∈G.

Свойство инвариантности классов естественно заложить в структуру аксиом классов (7.6) так, чтобы они не реагировали на групповые преобразования объектов. В этом случае объекты, отличающиеся друг от друга преобразованиями изданной группы G, будут классифицироваться как эквивалентные. Таким образом, задача формирования инвариантных понятий заключается в том, чтобы по заданной группе преобразований G построить аксиомы классов, способные безошибочно классифицировать все объекты, отличающиеся друг от друга преобразованиями g группы G.

Решение этой задачи сводится по существу к синтезу полных систем инвариантных предикатов (7.5). Если такие предикаты построены, то аксиомы классов вида (7.6) будут инвариантны, причем они обеспечат максимальную точность (экстраполирующую силу) описания классов при обучении по выборке минимального объема, содержащей по одному представителю из каждого класса. Заметим, что для достижения такой предельной точности в распознающих системах типа "перцептрон" [44, 133] может потребоваться обучающая выборка неограниченного объекта.

Многие традиционные методы формирования понятий [44, 133] основываются на построении их описаний в том или ином заранее выбранном классе функций. Такие описания определяют в пространстве признаков поверхности, разделяющие классы. Решающие предикаты (7.4) при этом строятся по обучающей выборке, а применяются к новым объектам. Поэтому весьма важно, чтобы решающие предикаты обладали высокой экстраполирующей силой не только на обучающей выборке, но и на всем множестве распознаваемых объектов.

Требование высокой экстраполирующей силы решающих предикатов в общем случае трудно формализуемо. Однако для некоторых конкретных классов функций увеличение экстраполирующей силы связано с минимизацией сложности описаний. Так, при синтезе полиномиальных описаний решение задачи сводится к построению полиномов минимальной степени с минимальным числом членов в разложении, обеспечивающего безошибочную классификацию элементов обучающей выборки [122].

В дальнейшем принцип минимальной сложности был положен в основу синтеза адаптивных логических решающих правил и реализующих их оптимальных распознающих графов [123]. В этом случае задача формирования понятий ставится так: по заданной обучающей выборке построить логические описания (аксиомы) классов А_k(ω) в терминах предикатов-признаков (7.5) такие, чтобы, во-первых, А_k(ω)=σ_k(ω) при всех ω∈ Ω₀ и, во-вторых, А_k(ω) имели минимальную (или близкую к минимальной) сложность. При выполнении этих двух условий естественно ожидать, что экстраполирующая сила (7.8) синтезированного логического описания классов будет достаточно высокой. В идеальном случае, когда распознаваемые классы не пересекаются в пространстве признаков, для получения максимальной экстраполирующей силы необходимо, чтобы синтезированные описания классов удовлетворяли условию (7.7).

Логические описания понятий в общем случае можно формировать в класс произвольных дизъюнктивных нормальных форм (д. н. ф.). По существу каждое такое описание аппроксимирует соответствующий неизвестный решающий предикат (7.4). Поэтому, коль скоро некоторое описание класса А_k(ω) построено, будем называть его идентифицирующим правилом k-го класса. Дизъюнкцию идентифицирующих правил всех классов будем называть распознающим (классифицирующим) правилом. Итак, задача обучения понятиям сводится к построению по обучающей выборке идентифицирующих правил минимальной сложности в классе д. н. ф. При этом сложность может трактоваться по-разному. Следует отметить, что именно требование минимальной сложности, позволяющее строить наиболее простые и информативные идентифицирующие правила, отличает предлагаемый подход от других методов формирования понятий, рассмотренных в работах [44, 133].

Распознающие правила иногда удобно строить в виде ориентированного графа - разветвленного дерева решений [123]. Узлам такого графа соответствуют некоторые предикаты-признаки; ветвям, исходящим из узла - возможные значения этих признаков. Все ветви заканчиваются листьями, которые ставятся соответственно номеру классов. Каждая ветвь, заканчивающаяся листом, содержит такую совокупность внутренних узлов, среди которых нет узлов, соответствующих одному и тому же значению предикатов. Д. н. ф., допускающие такое графическое представление, называется бинарно-древовидными [119].

Распознающее правило, представленное в форме бинарно-древовидной д. н. ф., будем называть последовательным распознающим правилом, а реализующий его граф типа "дерево классов" - распознающим графом. Процесс распознавания на таком "дереве классов" представляет собой последовательное "раскрытие" узлов графа, т. е. определение значений соответствующих предикатов на распознаваемом объекте. Любая ветвь на распознающем графе, соответствующая последовательности "раскрытых" узлов, приводит (с определенной вероятностью) к тому или иному классу.

Задача синтеза последовательных логических распознающих правил и реализующих их графов минимальной сложности сводится к построению бинарно-древовидной д. н. ф., обладающей теми же свойствами, что и описанные выше оптимальные идентифицирующие правила. Таким образом, возникает "последовательная" разновидность ранее сформулированной задачи формирования понятий: построить оптимальное распознающее правило, но не в классе д. н. ф., а в более узком классе бинарно-древовидных д. н. ф. Совершенно аналогично формулируются задачи синтеза понятий в тех случаях, когда признаки являются не двузначными, а многозначными предикатами [123].

Достоинством оптимальных идентифицирующих и распознающих правил является гарантируемая ими высокая точность распознавания при весьма экономном логическом описании классов и представлении соответствующих понятий. Это приводит в ряде случаев к значительной экономии времени и средств (в частности, памяти системы управления РТК), необходимых для распознавания различных классов объектов и ситуаций.

Для представления знаний в классах объектов внешней среды в виде формул исчисления предикатов можно использовать либо информацию, заключенную в обучающей выборке, либо словесное описание классов. С целью формализации процессов представления знаний введем обозначение

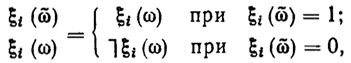(7.9)

где 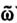- некоторый фиксированный объект, на элементах которого заданы значения предикатов-признаков (7.5).

Логическим описанием объекта © назовем элементарную конъюнкцию вида

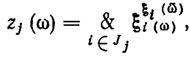(7.10)

где J_j - заданное множество индексов предикатов-признаков. Заметим, что предикаты ξ_i(ω) описывающие локальные свойства объектов, зачастую заданы не на всем объекте ω, а на некоторых его элементах ν⊂ω. В таких случаях логическое описание (7.10) имеет более сложный вид:

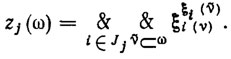(7.11)

Здесь ν - набор элементов объекта 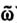, причем мощность множества J_j определяет ранг r логического описания, т. е. |J_j|=r.

Рассмотрим сначала индуктивный метод формирования понятий по обучающей выборке в виде д. н. ф. С этой целью построим таблицу, строки которой являются значениями предикатов-признаков и решающих предикатов на соответствующих элементах обучающей выборки Ω₀. Каждой строке полученной таблицы поставим в соответствие элементарную конъюнкцию z_h(ω) вида (7.10) и назовем ее аксиомой k-го подкласса, если σ_k(ω_h)=1. Объединяя все синтезированные таким образом аксиомы k-го подкласса z_h(ω), h=1,…,m_k, знаком дизъюнкции, получим описание k-го класса в виде аксиомы класса (7.5). Это и есть логическое представление понятия о k-м классе, которое система управления РТК формирует в процессе обучения.

Если набор предикатов-признаков таков, что отрицание любого из них есть либо другой предикат, либо выражается в виде дизъюнкции некоторых предикатов без отрицания, то в аксиому класса вида (7.6) достаточно включить не все исходные предикаты, а лишь те (назовем их позитивными предикатами), которые выполняются на каких-либо элементах обучающей выборки. Этот прием иногда позволяет существенно упростить вид аксиомы классов и уменьшить их ранг. Дело в том, что на практике каждый объект характеризуется лишь несколькими признаками-предикатами, а информация о том, что он не обладает остальными признаками, оказывается излишней. Описание классов в терминах только позитивных предикатов избавляет от необходимости хранить лишнюю информацию, что особенно важно с точки зрения минимизации потребной памяти и ускорения процессов распознавания.

Экстраполирующая сила (7.8) аксиом классов, т. е. способность правильно классифицировать объекты, не вошедшие в обучающую выборку, зависит от того, насколько полна информация о классах, содержащаяся в обучающей выборке Ω₀. Если обучающая выборка достаточно представительна и мощна, то индуктивное описание классов в виде (7.6), (1.10) будет правильно классифицировать все рассматриваемые объекты.

Однако на практике обучающая выборка зачастую оказывается не репрезентативной. В этих случаях она состоит из небольшого числа примеров (прецедентов) из каждого класса. Экстраполирующая сила системы аксиом, построенной по короткой обучающей выборке, обычно мала. Для увеличения экстраполирующей силы системы аксиом классов можно использовать рассматриваемые ниже оптимальные алгоритмы построения (по обучающей выборке) логических идентифицирующих и распознающих правил.

Качество обучения и точность распознавания существенно зависят от особенностей системы аксиом классов. Естественно потребовать, чтобы эта система обладала свойствами непротиворечивости и полноты. Кроме того, как уже отмечалось, практически важно, чтобы аксиомы классов были инвариантны по отношению к группам преобразования, действующим на объекты из соответствующих классов. Дадим строгую формулировку этих свойств.

Систему аксиом классов {А_k(ω)}^M_k=1 будем называть полной на множестве Ω, если для всякого элемента 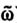∈ Ω найдется аксиома А_k(ω), классифицирующая 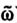, т. е. A_k(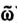) = 1.

Систему аксиом классов {A_k(ω)}^M_k=1 будем называть непротиворечивой на множестве Ω, если для всякого элемента 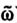∈ Ω из условия, что аксиомы A_i(ω) и A_j(ω) классифицируют 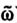, следует, что i=j. Заметим, что если свойство непротиворечивости имеет место на обучающей выборке, то это означает, что соответствующие обучающие подклассы не пересекаются. В этом случае непротиворечивость системы аксиом означает, что "эталонные" объекты из разных обучающих подклассов не имеют одинакового логического описания. Если же классы Ω_k, k = 1, ..., M, пересекаются, то целесообразно ввести новый класс Ω_M+1 - класс неоднозначно распознаваемых объектов. Это приводит к соответствующей модификации системы аксиом классов.

Аксиому класса А_k(ω) будем называть инвариантной относительно группы преобразований>G, если

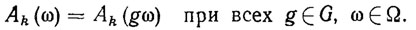(7.12)

В задачах распознавания сцен по их изображениям инвариантность аксиом классов играет важную роль. Дело в том, что изображения отдельных объектов на сцене часто подвергаются преобразованиям, имеющим групповую природу (сдвиг, вращение, проективные преобразования и т. п.). Ясно, что соответствующая аксиома класса не должна реагировать на указания преобразования g группы G. В результате в памяти системы управления РТК формируются понятия, инвариантные относительно той или иной заданной группы преобразований.

Достаточным условием инвариантности аксиомы класса A_k(ω) вида (7.6) относительно группы преобразований G является инвариантность относительно G всех входящих в нее предикатов-признаков. Заметим, что если два элемента ω_i, ω_j обучающей выборки Ω₀ отличаются преобразованием g∈G, т. е. ω_i=gω_j, то в аксиому класса (7.6) достаточно включить лишь одну аксиому подкласса, построенную по любому из этих элементов. Благодаря такой "инвариантной фильтрации" в процессе обучения понятиям строятся более простые логические описания классов. Инвариантность этих описаний по отношению к заданной группе преобразований G позволяет автоматически преодолеть трудности, связанные с возможными (может быть, неизвестными) преобразованиями объектов внешней среды. Тем самым существенно облегчается процесс распознавания сцен.

Таким образом, система управления РТК, реализующая описанные выше логические средства формирования понятий и представления знаний, автоматически строит (по обучающей выборке или исходя из априорного описания классов) проблемно ориентированную систему аксиом классов, обладающую свойствами полноты, непротиворечивости и инвариантности. Получающаяся в результате аксиоматическая система понятий выступает как эффективное средство логического представления знаний о внешней среде в памяти управляющей ЭВМ РТК.