7.5. Адаптивные решающие правила и фреймы

Для распознавания классов ситуаций и принятия адекватных решений системе управления РТК необходимо сформировать соответствующие решающие правила. Рассмотрим общую схему и конкретные алгоритмы синтеза и оптимизации адаптивных логических решающих правил. Принцип минимальной сложности, лежащий в основе их синтеза, обеспечивает простоту реализации и высокую экстраполирующую силу. Благодаря этим качествам адаптивные решающие правила находят все более широкое применение в ГАП, в частности, в РТК адресования деталей на конвейерах.

Рассмотрим сначала класс решающих правил, основанный на последовательном анализе информации. Синтез таких правил сводится к построению ориентированных графов типа "дерево решений" и к принятию решений с помощью таких распознающих графов. Это соответствует синтезу логических решающих правил в классе бинарно-древовидных д. н. ф. Процесс конструирования распознающих правил и графов по информации, заключенной в обучающей выборке, можно интерпретировать как процесс обучения распознаванию.

Предлагаемый подход к синтезу логических решающих правил и распознающих графов основывается на идее последовательной оптимизации конъюнкций предикатов-признаков по заданному критерию качества, вычисляемому по обучающей выборке. Общая схема такого синтеза заключается в следующем.

На k-м шаге рассматривается каждая конъюнкция z_k-1(ω) (k-1)-го ранга, построенная на предыдущем шаге. По этим конъюнкциям строятся новые конъюнкции z_k(ω) k-го ранга путем присоединения к z_k-1(&969;) ранее не использованных признаков ξ_i(ω) и их отрицаний 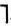ξ_i(ω). Среди полученных конъюнкций вида z_k-1 & ξ_i и z_k-1& Гξ_i отбирается наилучшая (в смысле заданного критерия качества)

На (k+1)-м шаге процесс повторяется. Окончание процесса определяется правилом остановки.

Для конкретизации описанной общей схемы построения логических решающих правил необходимо выбрать критерий качества и указать правило остановки алгоритма. Различные варианты такой конкретизации предложены в работах [119, 123, 133]. Поскольку в принципе возможны ошибки распознавания, целесообразно использовать статистические критерии качества (такие, например, как критерий Байеса или критерий Вальда). Наибольший практический интерес представляет критерий Байеса, так как он минимизирует вероятность ошибок. Согласно этому критерию, на k-м шаге отбирается тот признак, при включении которого в z_k(ω) максимизируется апостериорная вероятность некоторого класса, а именно:

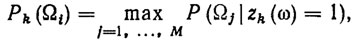(7.13)

Если для некоторой конъюнкции z_k(ω)k-го ранга P_k(Ω_i)=1, то дальше эта конъюнкция не достраивается. В этом случае она полностью характеризует класс Ω₀. Формализуем этот факт в виде импликации

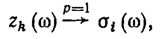(7.14)

представляющей собой достаточное условие принадлежности i-му классу.

Логическую функцию вида (7Л4) будем называть элементарным логическим решающим правилом, а совокупность таких правил, обеспечивающую безошибочную классификацию обучающей выборки, - полной и непротиворечивой системой логических решающих правил. Таким образом, задача обучения распознаванию сводится к построению полной и непротиворечивой системы элементарных логических решающих правил вида (7.14).

Описанный алгоритм последовательного построения такой системы является локально оптимальным в смысле максимизации на каждом шаге вероятности принадлежности объекта какому-либо классу согласно критерию (7.13). Однако апостериорные вероятности классов, входящие в этот критерий, на практике не-известны, поэтому эти вероятности приходится оценивать по информации, заключенной в обучающей выборке.

Пусть m_k(Ω₀) - число элементов обучающей выборки Ω₀, на которых z_k(ω)=1, a mⁱ_k(Ω₀) - число элементов Ω₀, принадлежащих классу Ω_j -, на которых z_k(ω)=1. Тогда искомые апостериорные вероятности могут быть оценены по обучающей выборке по формулам

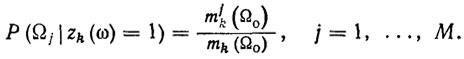(7.15)

Заметим, что оценки (7.15) тем точнее, чем больше объем m обучающей выборки Ω₀. (Здесь предполагается, что объекты ω поступают на вход информационной системы РТК случайным и независимым образом с некоторым, вообще говоря, неизвестным распределением вероятностей Р(ω)).

Необходимым условием построения полной и непротиворечивой системы логических решающих правил вида (7.14) является отсутствие пересечений обучающих подмножеств из Ω₀ в пространстве предикатов-признаков. Если такие пересечения имеются, то тем самым допускается некоторая вероятность ошибок. Однако при фактическом обучении РТК объекты, образы которых пересекаются в пространстве признаков, целесообразно исключить из обучающей выборки. В этом случае описанный выше локально-оптимальный алгоритм последовательного обучения заканчивает свою работу на некотором r-м шаге, причем r≤n. Результатом является полная и непротиворечивая система элементарных логических решающих правил вида (7.14).

Синтезированной системе соответствует распознающий граф типа "бинарное дерево классов". Каждое элементарное решающее правило вида (7.14) изображается ветвью этого графа. При этом признаку, входящему в конъюнкцию z_k(ω), соответствует узел на этой ветви, а решающему предикату σ_i(ω) соответствует лист с номером i. Из каждого узла исходят два ребра, соответствующие возможным значениям данного признака.

Алгоритм обучения на графе допускает следующую интерпретацию. На k-м шаге рассматривается каждая ветвь, построенная на предыдущем шаге. Если конъюнкция z_k(ω), соответствующая этой ветви, характеризует (с вероятностью 1) некоторый класс Ω_i, то ветвь заканчивается листом с номером i. В противном случае ветвь дополняется узлом, отобранным в соответствии с критерием и из этого узла строятся два новых ребра, отвечающих возможным значениям соответствующего признака.

Для распознавания класса, к которому принадлежит данный объект, нужно найти признак (или его отрицание), который присутствует во всех решающих правилах вида (7.14), и измерить его значение на данном объекте. В зависимости от полученного значения нужно далее рассмотреть то подмножество правил, которое содержит этот признак (или его отрицание). Описанный процесс повторяется, до тех пор, пока не останется только одно распознающее правило, которое и содержит ответ. Заметим, что в процессе распознавания ни один признак не измеряется дважды.

Если распознавание осуществляется по графу, то сначала измеряется признак, соответствующий узлу первого уровня. Далее по ребру, отвечающему полученному значению признака, осуществляется переход к узлу второго уровня и измерение соответствующего ему признака. Процесс "раскрытия" узлов по избранной ветви графа продолжается до тех пор, пока не встретится некоторый лист, который и содержит код искомого класса.

Введем следующие характеристики полной системы элементарных решающих правил:

1. ранг r - максимальный ранг конъюнкций z_k(ω) антецедентов в (7.14),
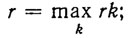
2. средний ранг r_ср, определяемый формулой 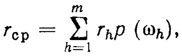где r_cp - ранг конъюнкции, характеризующей объект ω_h из Ω₀;
3. сложность N - общее число используемых признаков. Эти характеристики на распознающем графе, реализующем полную систему логических правил вида (7.14), интерпретируются так: r - максимальная длина ветви графа (r≤n); r_cp - средняя длина ветвей графа (r_cp≤r); N - общее число узлов графа.

Данные характеристики имеют следующий смысл: r - это максимальное число измерений предикатов-признаков, необходимых для распознавания любого объекта; r_cp - среднее число необходимых измерений; N - сложность реализации распознающего графа (например, в виде изоморфной этому графу микросхемы на логических элементах). Поэтому, чем меньше значения указанных характеристик, тем предпочтительнее (при прочих равных условиях) распознающий граф.

Полная и непротиворечивая система логических решающих правил обладает следующими свойствами. Во-первых, экстраполирующая сила системы на обучающей выборке максимальна, т. е. Е(Ω₀)=1. Во-вторых, конъюнкции-антецеденты системы

взаимно ортогональны (а следовательно, и статистически независимы). В-третьих, предикаты-признаки, не вошедшие ни в одно из элементарных правил вида (7.14), являются не информативными и могут быть отброшены. В-четвертых, ранг r и сложность N системы являются минимально необходимыми (при фиксированном локально-оптимальном алгоритме обучения) для безошибочной классификации обучающей выборки. В этом смысле можно считать, что синтезированная полная система логических решающих правил и реализующий ее распознающий граф имеют минимальную (или близкую к минимальной) сложность.

Разпознавание с помощью оптимальных правил и графов такого рода обычно не требует измерения всех предикатов-признаков (7.5), так как их ранг r, как правило, существенно меньше общего числа n предикатов. Это обстоятельство, выгодно отличающее логические решающие правила и графы от традиционных методов "перцептронного" распознавания, использующих одновременно все признаки, особенно важно в тех случаях, когда "стоимость" измерений предикатов-признаков достаточно высока. Наглядность, простота и последовательный характер принятия решений на синтезированных распознающих графах типа "дерево классов" делает их удобным инструментом автоматического распознавания в системах управления РТК.

Рассмотрим теперь задачу построения и оптимизации идентифицирующих правил, аппроксимирующих решающие предикаты (7.4). Особенность этой задачи заключается в том, что она решается для каждого класса в отдельности. Полная система синтезированных идентифицирующих правил в принципе позволяет распознать любой объект. Для увеличения экстраполирующей силы такой системы важно, чтобы каждое входящее в нее правило A_i(ω) имело, по возможности, минимальные ранг r_i и сложность N_i. Подобные идентифицирующие правила будем называть оптимальными.

Общая схема локально-оптимального (в смысле байесовского критерия качества) алгоритма синтеза идентифицирующих правил в виде д. н. ф. заключается в следующем. Рассматривается некоторый класс Ω_i и соответствующее ему подмножество элементов обучающей выборки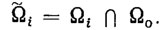

На первом этапе последовательно строятся всевозможные конъюнкции z_k(ω) k-го ранга (k=1, 2, ...) и для каждой из них по формуле (7.15) вычисляется апостериорная вероятность i-го класса. Как только при некотором k=r₁ окажется, что Р₁(Ω_i)=1, то соответствующая конъюнкция z_r1(ω) ранга>r₁ запоминается как первый дизъюнктивный член искомого идентифицирующего правила. (Если среди конъюнкций r₁-го ранга таких конъюнкций окажется несколько, то среди них отбирается та, которая характеризует максимальное число объектов из Ω_i). Далее из множества Ω_i исключаются все объекты, охарактеризованные отобранной конъюнкцией z_r1(ω). Обозначим полученное подмножество через Ω,sup>1_i

На втором этапе на подмножестве Ω¹,sub>i вновь последовательно строятся всевозможные конъюнкции z_k(ω) ранга k≥r₁ и среди них отбирается такая, что Р_r2(Ω_i)=1. Эта конъюнкция z_r2(ω) ранга r₂ дизъюнктивно добавляется к ранее отобранной конъюнкции z_r1(ω). Далее строится подмножество Ω²_i путем исключения из множества Ω'_i всех элементов, охарактеризованных новой конъюнкцией z_r2(ω).

Описанный процесс продолжается до тех пор, пока на некотором шаге N_i множество Ω_i^N_i не окажется пустым.

Результатом работы данного алгоритма является аксиома i-го класса вида

(7.16)

обладающая следующими свойствами:

1. A_i(ω)=1 при всех ω∈ Ω_i;
2. ранг r_i аксиомы A_i(ω) является (при данном байесовском алгоритме обучения) минимально необходимым для того, чтобы она полностью характеризовала все элементы подмножества Ω_i, причем сложность N_i аксиомы как функция ее ранга r_i также минимальна;
3. в процессе построения аксиомы класса A_i(ω) происходит "естественный отбор" (селекция) информативных признаков, в то время как не информативные признаки автоматически отбрасываются.

На основе синтезированных аксиом классов вида (7.16) непосредственно получаем следующую полную и непротиворечивую систему идентифицирующих правил:

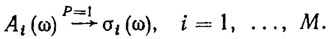(7.17)

Идентифицирующее правило вида (7.17) может быть представлено в виде ориентированного графа такого же типа, как и распознающий граф. Отличительной чертой идентифицирующего графа является то, что все его листья относятся к одному и тому же классу. Каждой конъюнкции z_rj(ω) аксиомы i-го класса соответствует ветвь графа, каждому признаку ξ_i(ω) - узел и каждому значению признака - ребро, исходящее из соответствующего узла.

Совокупность идентифицирующих графов удобно представлять в виде "орбитального" графа классов. На нулевой орбите этого графа располагаются листья с указанием номеров всех классов. На первой орбите располагаются узлы первого уровня идентифицирующих графов, на второй орбите - узлы второго уровня и т. д. Из свойств синтезированных аксиом классов следует, что число орбит r_i, используемых при графическом представлении k-го класса, минимально. При этом числе орбит используется минимальное число ветвей N_i Конъюнкции, соответствующие различным ветвям, взаимно ортогональны. Это говорит об их статистической независимости и высокой информативности.

Для идентификации данного класса нужно выбрать соответствующее идентифицирующее правило (или реализующий его идентифицирующий граф). Далее нужно проверить на данном объекте истинность конъюнкций, входящих в аксиому рассматриваемого класса. Если хотя бы одна из этих конъюнкций истинна, то объект идентифицируется как представитель данного класса. В противном случае можно только сказать, что он не принадлежит данному классу.

Процесс идентификации по графу соответствует "раскрытию" его узлов, начиная с первой орбиты. На первом шаге вычисляется значение признака, отвечающего первому узлу. Если это значение соответствует исходящему из узла ребру, то следует измерить значение признака, отвечающего узлу второй орбиты, к которому ведет данное ребро, и т. д. Если таким образом удается дойти до конца какой-либо ветви, то идентифицируемый объект относится к соответствующему классу. Если же ребро, соответствующее вычисленному значению очередного признака, отсутствует, то это значит, что исследуемый объект данному классу не принадлежит. Для распознавания объекта к нему нужно применять последовательно оставшиеся графы до тех пор, пока на некотором из них не произойдет идентификация классов.

Экстраполирующая сила синтезированных оптимальных идентифицирующих правил и графов достаточно высока. Это следует из того, что ранг r_i и сложность N_i каждой аксиомы класса A_i(ω) минимальны с точки зрения обеспечения естественного требования Е(Ω₀)=1 при заданном алгоритме обучения, основанном на критерии Байеса. Этот вывод подтверждается также практическими результатами решения разнообразных задач распознавания и идентификации классов. Некоторые из этих результатов рассмотрены в п. 7.7.

В заключение укажем на связь синтезированных решающих правил с фреймами М. Минского [71]. В предисловии к книге [71] Г. С. Поспелов пишет: "...фрейм любого вида - это та минимально необходимая структурированная информация, которая однозначно определяет данный класс объектов. Наличие фрейма позволяет относить объект к тому классу, который им определяется". Данное определение весьма точно выражает сущность синтезированных адаптивных логических решающих правил минимальной сложности. Поэтому сами эти правила и определяемые ими описания классов можно условно назвать логическими фреймами.

В общем случае фреймы представляют собой совокупность знаний о достаточно сложных объектах и ситуациях. Поэтому они содержат не только локальные сведения о конкретных объектах, которые можно представить с помощью логических описаний в терминах предикатов-признаков, но и знания о возможных действиях и условиях их применимости. Кроме того, фреймы содержат некоторые "дыры", называемые слотами, которые заполняются по мере конкретизации знаний в процессе решения задач.

Удобной формой записи фреймов являются семантические сети, дополненные описаниями возможных действий и условий их применимости. Первоначально семантические сети использовались лингвистами для представления смысла текста естественного языка. В дальнейшем появилось много разновидностей таких сетей. Общим для них является то, что вершины сетей соответствуют некоторым объектам, а дуги - отношениям между соответствующими объектами. Иногда вершины представляют сложные отношения между объектами. В этом случае такие вершины соединяются дугами с теми объектами, которые связаны данным отношением. Часто для наглядности на дугах отмечается, какую роль играет каждый объект или отношение.

Важным достоинством семантических сетей является то, что представляемые ими знания хорошо поддаются обработке на ЭВМ. Это обеспечивается явным заданием связей между объектами и позволяет расшифровать смысл текста, заданного семантической сетью. Семантическая сеть может описывать класс объектов или ситуаций. В этом случае она имеет вид распознающего или идентифицирующего графа. Однако знания такого рода для РТК носят фрагментарный характер. Они, как правило, недостаточны для организации целенаправленного функционирования РТК. Тем не менее эти фрагментарные знания могут с успехом использоваться для синтеза правил поведения РТК типа "класс ситуаций- действие". Такие правила-фреймы позволяют организовать целенаправленное адаптивное поведение РТК в не детерминированной и изменяющейся производственной обстановке. Например, в РТК распознавания и адресования деталей на подвесном конвейере в качестве "класса ситуаций" может использоваться аксиома класса деталей A_k(ω), а в качестве "действия" - сигнал на приводы стрелок ответвления, обеспечивающий адресование (и доставку) деталей k-го класса на соответствующие позиции сборочного конвейера [103].