2.6. Линеаризация и делинеаризация

Эти операции не так просты, как остальные натуральные операции, и, пожалуй, утверждение о том, что без умения выполнять эти операции нельзя понимать математику, не так уже бесспорно. Но во всяком случае, не умея выполнять эти операции, невозможно решить многие практические задачи. Это с полной определенностью следует из известного основополагающего труда А. А. Маркова [9].

А. А. Марков разработал теорию частного вида алгоритмов, названных им нормальными, которые описывают преобразования слов. Чтобы нормальные алгоритмы применить для преобразования других конструкций, нужно эти конструкции сначала превратить в слова (линеаризовать), а потом результаты превратить в конструкции соответствующего класса (делинеаризовать). Марков, которому линеаризация и делинеаризация как общие операции были еще неизвестны, полагал, что в каждом частном случае человек сумеет произвести такие превращения. Но перед нами стоит более трудная задача. Нам может потребоваться устройство, которое выполняло бы эти операции без участия человека. Поэтому нам необходимо математическое описание линеаризации и делинеаризации, пригодное во всех мыслимых случаях.

В процессе выполнения линеаризации и делинеаризации применяется операция произвольного выбора элемента конечного множества. В традиционной теории алгоритмов эту операцию тщательно избегали из-за неопределенности ее результата. Но оказывается, неопределенность можно устранить, сочетая произвольный выбор с некоторыми другими операциями. Мы будем его применять только в составе произвольной нумерации элементов множества, а устранять - построением всех мыслимых нумераций и выбора только одной вполне определенной.

Опишем процесс подробнее. Номера будем представлять в виде слов, составленных из одинаковых букв, например из букв вида "|" (палочка). Количество букв в слове и будет являться номером. Предположим, что нумеруемое множество содержит n элементов.- Теперь построим результат всех возможных нумераций. Для этого снимем копию с перенумерованного множества, а в нем произведем перестановку номеров. Повторяем процесс до тех пор, пока все возможные нумерации не будут получены. В конце процесса мы будем иметь и! перенумерованных множеств. Этот результат уже не является неопределенным. Перестановки номеров можно производить с помощью специальной функции, которая может быть всегда построена сразу же после окончания случайной нумерации. Очень важно, что эта функция не должна быть обязательно заранее заготовлена, так как тогда наш метод не был бы универсальным (потому что потребное число таких функций не ограничено: для каждого п требуется своя функция).

Покажем, как строится функция, преобразующая нумерацию. Через j обозначим номер системы нумерации, считая, что j = 1 для произведенной нами произвольной нумерации. Очевидно, 1≤j≤n!≤. Через i обозначим произвольный номер элемента. Искомуя функцию обозначим через φ(i, j). Ее значением является номер при j-й нумерации этого элемента, который при случайной нумерации получил номер i. Функция φ(i, j) может быть задана таблично. Определяющую ее таблицу построим, выполняя процесс, описанный ниже.

1°. Записать строку чисел, состоящую из единственного числа 1. Перейти к п. 2.

2°. Полагать k = 1. Перейти к п. 3.

3°. К каждой из имеющихся k! строк приписать справа число k+1. Перейти к п. 4.

4°. Для каждой из имеющихся k! строк составить еще по к строк путем обмена местами числа k+1 последовательно с каждым из чисел, стоящих слева от него. Перейти к п. 5.

5°. Если k+1 = n, то процесс окончен; иначе - перейти к п. 6.

6°. Увеличить значение k на 1. Перейти к п. 3.

После выполнения описанного правила мы получим n! строк, состоящих (каждая) из чисел 1, 2,..., n, расположенных различным образом. Запишем эти строки друг под другом так, чтобы получилась таблица из n столбцов и n! строк. Номер столбца будем считать значением i, а номер строки - значением j. Числа, расположенные в этой таблице, будем считать значениями Функции φ(i, j).

Пример 2.1. Дано множество из трех элементов {а, б, в} и результат произвольной нумерации

Построим для n = 3 функцию φ и с ее помощью определим пятый вариант нумерации.

Составляем строку из одной цифры (в соответствии с п. 1⁰):

Полагаем k = 1 (в соответствии с п. 2°). К каждой из имеющихся строк, количество которых k! = 1! = 1, приписываем число k+1 = 2 (в соответствии с п. 3 ). Получаем строку

В силу п. 4° строим еще одну строку, переставляя 2 с числом, стоящим слева от него. Теперь имеем две строки

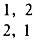
Так как (см. п. 5°) k+1 = 2≠3 = n, то увеличиваем к на единицу, т. е. делаем k = 2 и переходим к п. 3.

Далее к каждой из имеющихся в количестве k! = 2! = 2 строк приписываем число k+1 = 2+1 = 3. Получаем

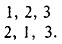
Для каждой из этих строк (в соответствии с п. 4⁰) составляем еще по k = 2 строки путем обмена тройки с числами, стоящими слева от нее. Получаем всего шесть строк

В соответствии с п. 5⁰ прекращаем процесс, так как k+1 = 2 + 1 = 3 = n.

Теперь строим таблицу значений функции φ (i, j) (табл. 2.1).

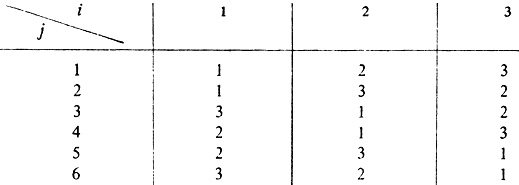
Таблица 2.1. Значения функции φ (i, j) для n = 3

Из этой таблицы видно, что φ (1, 5) = 2; φ(2, 5) = 3; φ(3, 5) = 1. Искомый пятый вариант нумерации в нашем случае будет

Теперь, перейдем к рассмотрению операции линеаризации. Пусть К - некоторая конструкция класса (А, В, ∑), где А - алфавит букв, В - алфавит связей, ∑ - алфавит оболочек (содержит одну оболочку, т. е. одну группировочную букву и одну группировочную связь). Как известно, эти алфавиты между собой не пересекаются. Включим группировочную букву в качестве последней в алфавит А, а группировочную связь в качестве последней в алфавит В. Новые алфавиты обозначим соответственно через А' и В'. Выберем алфавит С, не пересекающийся ни с А' , ни с В', число букв которого равно наивысшему жанру связей, описанных в В'. Кроме того выберем однобуквенный алфавит D, не пересекающийся ни с А', ни с В', ни с С. Для определенности положим, что D = |. Выбрав эту именно букву, мы нисколько не уменьшаем общности наших рассуждений, так как если бы она входила в один из алфавитов А', В' и С, то вместо нее мы взяли бы другой символ.

Образуем новый алфавит Е = А'∪B'∪C∪D. В результате линеаризации нами будет получено слово в Е. Это значит, что, если в некоторой области применения должна использоваться линеаризация, то набор символов заранее должен быть выбран достаточно обширным.

Для удобства дальнейшего описания условимся буквы алфавита А' обозначать а₁, а₂, ..., а_n, буквы алфавита В' (т. е. обозначения связей) - b₁, b₂, ..., b_m, буквы алфавита С - с₁, с₂, ..., с_r. В дальнейшем нам придется слова в алфавите Е сравнивать по их алфавитному порядку. Я предполагаю, что понятие алфавитного порядка читателю известно; это тот порядок, в котором слова располагают в словарях и энциклопедиях. Если мы имеем два слова в одном и том же алфавите, то они называются равными, если состоят из одинаково расположенных попарно одинаковых букв. Если они не равны, то всегда одно из них по своему алфавитному порядку предшествует другому. При этом предшествующее будем называть младшим, а последующее старшим. Одно слово нестарше другого, если оно либо младше него, либо равно ему. Только слова в одном и том же алфавите допускают сравнение по алфавитному порядку.

Линеаризация производится так.

I этап. В конструкции К все оболочки представляют в виде группировочных букв с "исходящими" из них группировочными связями.

II этап. Нумерация связей. Сначала нумеруются все связи, присутствующие в K и одинаковые с b₁, затем все связи, одинаковые с b₂, и т. д., пока не будет исчерпан алфавит В'. При этом после каждой произвольной нумерации конструкцию копируют и строят новые ее экземпляры со всеми возможными нумерациями связи данного вида. Каждую новую нумерацию производят для каждой из полученных конструкций. После окончания этого этапа число символьных конструкций со связями, помеченными номерами, равно N₁!*N₂!...*N_m!, где N_i - количество связей вида b_i, содержащихся в исходной инструкции. Номера представлены строками, составленными из букв в алфавите D.

III этап. В каждой из имеющихся конструкций ветви связей помечают буквами в алфавите С: ветви 1-го жанра буквой с₁, 2-го жанра - буквой с₂, и т. д., r-го жанра - буквой с_r.

Имея много конструкций, мы дальнейший процесс описываем только для одной, так как для всех конструкций он аналогичен, и сохраняем для этой конструкции обозначение К.

IV этап. Нумерация ветвей связей. У каждой связи просматривают ветви и помеченные одинаковыми буквами нумеруют. Например, если буквой с2 помечена в данной связи только одна ветвь, ей присваивают номер |, если же - три ветви, то они получают номера |, || и |||. После каждой случайной нумерации строят результаты всех возможных нумераций.

После выполнения предыдущих этапов каждая ветвь получила обозначение в виде слова, построенного так: b_i1| ... |c_j1| ...|. Замечу, что в пределах одной конструкции нет двух ветвей, имеющих одинаковое обозначение, и все обозначения имеют разный алфавитный порядок. Так, если связь b, а ее ветвь с, причем номер связи 2, а номер ветви 3, то обозначением ветви будет b||с|||. Обозначения ветвей связей будем называть их именами.

V этап. Для каждой конструкции К строят слово специального вида следующим образом.

Просматривают алфавит В', пока не найдут в нем букву, такую, что в К содержится отвечающая ей связь (с номером I). Находят младшую из ветвей этой связи (в смысле алфавитного порядка имени этой ветви) и тем самым некоторую букву конструкции. Пусть это будет a_i1. Выписывают в порядке возрастания алфавитного старшинства относительно Е сначала имена всех "входящих" ветвей группировочных связей, связывающих эту букву (если такие имеются), а затем - всех остальных ветвей. После этого выписывают букву a_i1. Полученная строка называется фрагментом. Фрагментом назовем также слово, которое образуется в результате присоединения к фрагменту еще одного фрагмента, содержащего одну букву в А'. Далее имена ветвей будут временно помечаться, например чертой снизу. Просматривая фрагмент слева направо, находят в нем имя ветви, которое еще не подчеркнуто (а вначале они все неподчеркнуты), и подчеркивают его. Это имя позволяет найти в конструкции связь, которой принадлежит ветвь, имеющая указанное имя. Самая младшая из еще неиспользованных ветвей этой связи, укажет нам новую букву a_i2, для которой нужно точно так же, как описано выше, построить элементарный фрагмент и приписать его к ранее полученному.

Если бы оказалось, что в конструкции все ветви данной связи уже исчерпаны, мы, двигаясь по фрагменту (слева направо), подчеркнули бы следующее имя связи и повторили исследование конструкции.

Процесс оканчивается, когда в фрагменте нечего больше подчеркивать (неподчеркнутые имена ветвей исчерпались).

VI этап. После V этапа получено довольно многочисленное, но конечное множество фрагментов, в каждом из которых все имена ветвей подчеркнуть. Отбрасываем все подчеркивания. Имеем множество слов специального вида. Из них выбираем любое, которое в алфавите Е нестарше всех других. Это слово Является результатом линеаризации.

Укажем ряд свойств линеаризации, которые при желании можно было бы математически доказать. >

1. Если заданы непересекающиеся алфавиты А, В, ∑, С и Д то результат линеаризации каждой конструкции - единственный.
2. В результате линеаризации после каждой группировочной буквы непосредственно расположены элементарные фрагменты сгруппированных ею букв.
3. Порядок символов в алфавитах А и В существенно влияет на результаты линеаризации (кроме отдельных частных конструкций).
4. Описанный процесс неприменим к конструкциям, не содержащим связей: однобуквенным и пустым.

Будем считать результатом линеаризации однобуквенной или пустой конструкции, не содержащей связей, соответственно однобуквенное или пустое слово.

В практике линеаризацию в чистом виде применяют редко. Обычно ее сочетают с другими операциями и, объявляя это сочетание новой операцией, имеют более простую операцию. В частности, полученный результат можно сжать, заменяя в нем группировочные буквы парами скобок "("и")". Делают это в несколько приемов.

а⁰. В результирующем слове находят группировочную букву, не группирующую других группировочных букв, т. е. такую, что ни одному принадлежащему ей имени "исходящей" ветви группировочной связи не соответствует имя "входящей" ветви той же связи, принадлежащее группировочной букве.

б⁰. Символ ")" вставляют после последней буквы из сгруппированных выбранной группировочной буквой. Удаляют все имена ветвей, связей, изображающих группировку с помощью указанной группировочной буквы, и, наконец, ее саму заменяют символом "(". Всю строку вместе с охватывающими ее скобками при дальнейшем выполнении процесса считают одной буквой.

в⁰. Если еще не все группировочные буквы исключены, то возвращаются к п. а⁰. Иначе процесс окончен.

Иногда бывает удобно иметь несколько видов оболочек. В этом случае следует ввести несколько группировочных букв, тогда как группировочные связи все могут быть однотипными.

Теперь коротко опишем делинеаризацию применительно к исходному слову, принадлежащему множеству слов, полученному выше после выполнения

V этапа. Она применима к любому из них, а также к однобуквенному слову и к пустому. Будем считать, что известны алфавиты А, В, ∑, С и D. По определению результатом делинеаризации пустого слова является пустая конструкция, а однобуквенного слова - входящая в него буква.

В общем случае делинеаризация производится так:

1°. Все связи следования в преобразуемом слове помечаются новым вспомогательным знаком (например, птичкой).

2°. Находят в операнде имена ветвей, принадлежащих какой-нибудь связи (имеющих одинаковую букву в В' и одинаковый номер за ней). Связывают соответствующие этим ветвям буквы в А' связью необходимого типа, способом, который задается именами ветвей. Сжимают операнд, удаляя из него, использованные имена ветвей. Процесс повторяют, пока из оперенда не будут удалены все имена ветвей.

3°. Все связи следования, помеченные птичками, удаляют.

После этого процесса будет получена искомая конструкция.

Обозначим делинеаризацию через d (Р), где Р - слово специального вида, а линеаризацию - через l (K), где K - произвольная конструкция.

Если l(K₁) = l(K₂), то конструкции K₁ и K₂ называются одинаковыми и при этом пишут K₁ = K₂. Выбор алфавитов С и D не влияет на одинаковость конструкций.

Легко видеть, что

но равенство

может быть и неправильным.

Операция линеаризации важна тем, что позволяет эффективно узнавать, одинаковы ли конструкции. Как читатель увидит в дальнейшем, линеаризация и делинеаризация очень важны при построении общего определения алгоритма, а значит и общей теории роботов.