2.5. Операции над символьными конструкциями

Комбинация сигналов - это символьная конструкция. Как мы уже знаем, информация всегда существует в виде некоторой комбинации сигналов, т. е. в виде некоторой символьной конструкции.

Преобразованием символьной конструкции называется всякое внесение в нее изменений, результатом которого является опять символьная конструкция.

Иногда бывает задано какое-либо условие. Проверить, выполнено ли оно для рассматриваемой символьной конструкции,- это значит, не изменяя конструкции, поставить ей в соответствие так называемую логическую букву, т. е. либо букву, предназначенную для обозначения слова "истина" (если условие выполнено), либо другую букву, означающую "ложь" (если условие невыполнено). Рассматриваемая символьная конструкция всегда бывает под-конструкцией некоторой более обширной конструкции, остальные части которой мы не рассматриваем. "Поставить в соответствие" - это значит связать логическую букву с, "невидимой частью" этой более обширной конструкции. Проверка выполнения условия называется логическим действием.

Естественно, что как преобразование символьной конструкции, так и логическое, действие над ней можно описать в виде соответствующего конкретного правила. Иногда удается составить такое правило сразу для целого множества символьных конструкций. В этом случае преобразование или логическое действие называют массовым. Именно массовые преобразования и логические действия имеют большое значение, и в дальнейшем речь пойдет только о них.

Термин "массовый" носит чисто условный (а вернее - математический) смысл. Он ничего не говорит о виде множества исходных конструкций, которое, в принципе, может быть бесконечным, конечным, одноэлементным и даже пустым.

Очевидно, последовательность преобразований, в ходе которой, возможно, производились и логические действия с целью выбора дальнейших преобразований, тоже является преобразованием. Точно так же снятие копии с исходной конструкции, преобразование этой копии, выполнение логического действия над результатом преобразования и отнесение полученной логической буквы к исходной конструкции тоже является логическим действием. Таким образом, преобразования и логические действия могут быть не только одношаговыми, но и многошаговыми.

Преобразования и логические действия, которые для любого допустимого исходного данного являются одношаговыми, называются операциями. С точки зрения математики между одношаговыми и многошаговыми преобразованиями и логическими действиями нет особой разницы. И те и другие являются функциями (или, что то же, однозначными отображениями), которые любому допустимому исходному данному ставят в соответствие определенный результат. Иное дело приложения к робототехнике. Здесь преобразования и логические действия выполняются устройствами. Очень существенно, требуется ли выполнить один шаг или тысячу (расходуется различное время!).

На практике существует возможность многошаговое преобразование или логическое действие превратить в одношаговое (в операцию) путем замены применяемого устройства. В нашей теории это учитывается в виде волевого акта - объявления какого-либо многошагового преобразования или логического действия операцией.

Совокупность множества символьных конструкций некоторого класса (А, В, ∑), множества операций и множества правил (их называют алгоритмами), определяющих многошаговые преобразования и логические действия, будем называть областью применения. Этот термин мы уже раньше использовали без его точного разъяснения.

Каждая область применения скрывает за собой некоторую систему управления или класс таких систем. Объявляя новую операцию, мы переходим в новую область применения. Операции являются в ней простейшими преобразованиями и логическими действиями, но за этой простотой в других областях применения могут скрываться очень сложные многошаговые процессы.

После приведенных разъяснений перейдем к точным математическим определениям операций, которые позволят нам иметь дело с любыми областями применения.

Простейшими считаются так называемые натуральные операции, получившие свое название потому, что умение их выполнять постулируется. Кто не обладает этим умением, вообще не может изучать математику. К тому же техника располагает простыми устройствами для их выполнения. Натуральные операции задаются непосредственным описанием каждой из них.

При описании натуральных операций мы встретимся с простой символьной конструкцией, известной под названием "квазислово".

Квазисловом называется символьная конструкция, которая отличается от слова тем, что одна из букв в ней связана специальной связью (которая называется выделяющей), имеющей первый ранг и первый жанр. Кроме связей следования в каждом квазислове присутствует одна выделяющая связь. Связанная ею буква называется выделенной. Квазислово не может быть пустой конструкцией.

Квазислово, полученное из слова

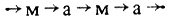
путем выделения второй буквы, представляет собой конструкцию

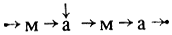
Приведем перечень и описание натуральных операций, объединяя их в группы в зависимости от вида исходного данного и результата.

I. Операции вида "слово → слово":

1. Аннигиляция. Однобуквенное слово преобразуется в пустое слово. На практике этой операции соответствует стирание однобуквенного слова.

2. Генерация однобуквенного словах. Пустое слово преобразуется в одно-буквенное слово JC (при указании этой операции буква, входящая в х, должна быть задана). На практике этой операции соответствует написание одно-буквенного слова на чистом листе бумаги.

3. Сцепление двух слов. Иногда эту операцию называют конкатенацией. Если даны два непустых слова, то эта операция заключается в замене заканчивающей связи первого слова и начинающей связи второго одной продолжающей связью. Исходным данным этой операции является упорядоченная пара непустых слов, а ее результатом - одно слово. С операциями над упорядоченными парами операндов каждый из нас знаком. Например, такой является в арифметике операция вычитания. Операция, выполняемая над упорядоченной парой операндов, называется двухместной, бинарной или операцией второго ранга. Все прочие натуральные операции выполняются над одним операндом. Такие операции называются одноместными, унарными или операциями первого ранга.

Пример. В результате сцепления слов

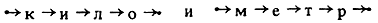
получится результат

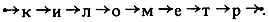
II. Операции вида "слово ↔ квазислово":

4.Нахождение начала слова. Непустое слово преобразуется в квазислово с выделенной первой буквой.

Пример. Здесь и дальше связи следования в словах и квазисловах опускаются. Слово

после нахождения начала преобразуется в квазислово

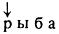
5. Отключение. Рассматриваемое квазислово путем отбрасывания выделяющей связи преобразуется в слово.

Пример. Квазислово

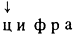
с помощью операции отключения преобразуется в слово

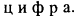
III. Операции вида "квазислово → квазислово":

6. Продвижение вправо. В преобразуемом квазислове выделяющая связь переносится на одну букву вправо.

Пример. Квазислово

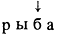
при продвижении вправо преобразуется в квазислово

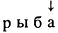
К квазислову

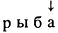
эта операция неприменима (некуда перенести выделяющую связь).

7. Продвижение влево. В преобразуемом квазислове выделяющая связь переносится на одну букву влево.

Пример. Квазислово

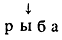
при продвижении влево преобразуется в квазислово

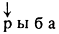
а к последнему квазислову ее применить нельзя (некуда перенести выделяющую связь).

8. Продолжение квазислова буквой х. Операция может быть применена только к квазисловам, в которых выделена последняя буква. Заключается она в том, что после выделенной буквы приписывается буква х. Для каждого такого преобразования должна быть задана конкретная буква, являющаяся значением х.

Пример. Продолжение квазислова

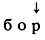
буквой "т" дает квазислово

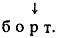
9. Отбрасывание конца. Все буквы, следующие за выделенной буквой преобразуемого квазислова, отбрасываются.

10. Замена буквой х (где x - произвольная конкретная буква). Выделенную букву преобразуемого квазислова заменяют буквой х, которая становится выделенной.

Пример. Квазислово

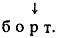
после замены буквой л преобразуется в квазислово

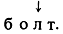
IV. Операции вида "конструкция ↔ слово":

11. Линеаризация. Произвольная конструкция преобразуется в слово специального вида (эта операция подробно описана в § 2.6).

12. Делинеаризация. Операция, обратная линеаризации. С ее помощью слова специального вида преобразуются в конструкции (см. § 2.6).

V. Логические натуральные операции:

13. Проверка непустоты. Соответствующее ей условие гласит: "Данное слово непусто".

14. Проверка начала. Соответствующее условие гласит: "В данном квазислове выделена первая буква".

15. Проверка конца. Проверяемое условие гласит: "В данном квазислове выделена последняя буква".

16. Проверка одинаковости букв. Условие гласит: "В данном квазислове выделенная буква одинакова с буквой х." В качестве х может быть задана любая буква.

Дадим общее определение операции. Операцией называется или 1) натуральная операция или 2) отображение, соответствующее определенному (уже разработанному) алгоритму, объявленное операцией.

Для того чтобы понять это определение, нужно ознакомиться с точным смыслом слова "алгоритм". Мы это узнаем в гл. 4. Пока что ограничимся неточным смыслом этого слова:, алгоритм - это многошаговое преобразование символьной конструкции или многошаговое логическое действие. Из гл. 4 нам станет ясно, что все операции, какие только возможны, конструируются из натуральных операций путем построения алгоритмов и объявления новых операций.