2.4. Связи и отношения

Современная абстрактная алгебра рассматривает связи как отношение между связываемыми ими элементами. Алгебра потому и называется абстрактной, что, изучая различные объекты, оставляет в стороне все их свойства, которые в этой науке считаются несущественными. Понятие отношения в абстрактной алгебре выглядит так. Предположим, что М - некоторое множество. Образуем всевозможные наборы по и элементов этого множества. В каждом наборе считается, что каждый из вошедших в него элементов стоит на определенном месте. Например, если множество состоит из букв "а", "б", "в", "г", "д", то при n = 3 из элементов этого множества можно образовать наборы (а, а, а), (а, а, б),... , (а, б, в),..., (д, д, д).

Но вернемся к общему случаю. Множество всех наборов по п элементов обозначают Мⁿ. Его элементами являются указанные наборы. Предположим теперь, что Φ - некоторое подмножество множества Мⁿ. Тогда о членах каждого набора n элементов множества М, если набор принадлежит Φ, говорят, что они находятся в отношении Φ. Например, если (x₁, x₂, ..., x_n) ∈Φ, то x₁, x₂, ..., x_n находятся в отношении Φ. При этом пишут Φ (x₁, x₂, ..., x_n). Отношение Φ называют n-местным.

Для того чтобы ввести понятие одноместного отношения, полагают, что М' = М. Элементами М являются "наборы" вида (а₁), (а₂), ..., где а₁, а₂, ... - элементы множества М. Другими словами, каждый набор, входящий в М , является элементом множества М. Любое подмножество множества М', а значит и множества М, является одноместным отношением, заданным на М.

Предположим, что φ - такое подмножество. Если некоторый х - элемент множеств; М удовлетворяет этому отношению, т. е. если х ∈ φ, то пишут φ(х).

Одноместные отношения называют унарными, двухместные - бинарными, трехместные - тернарными.

Понятия множества и отношения в настоящее время широко известны, и люди, занимающиеся наукой, любят применять абстрактную алгебру и, в частности, эти понятия. Они считают это признаком солидности. У таких любителей абстрактной алгебры может возникнуть вопрос "почему мы ею не пользуемся?" Ответ прост: абстрактная алгебра для описания символьных конструкций неудобна, неплодотворна. Покажем это на простейшем примере.

В качестве символьной конструкции рассмотрим слово

Указывая явно все связи между буквами, получаем

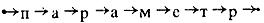
Это и есть самое полное описание данной символьной конструкции. Опишем ее теперь средствами абстрактной алгебры. Для этого представим ее в виде множества, на котором заданы некоторые отношения. Все элементы множества должны быть различны; чтобы этого добиться, нужно или снабдить одинаковые буквы пометками, либо ввести унарные отношения, которые говорили бы о том, какую букву обозначает элемент множества. При этом нужно помнить, что порядка среди элементов множества нет и его наглядно можно представить себе так:

На этом множестве должны быть заданы два одноместных отношения, позволяющих найти начало и конец слова, и одно бинарное отношение, показывающее, как буквы следуют друг за другом. Эти отношения будут иметь вид:

Кроме того, должно быть задано отношение равенства букв

Итак, слово "параметр" имеет алгебраическую структуру, т. е. является совокупностью вида (М, Н, К, С, Р). Простота последней записи иллюзорна. Ведь для ее понимания нужно знать и все предыдущие записи.

Мы рассмотрели первую из вышеуказанных возможностей; рассмотрим вторую. Пусть теперь слово представлено в виде множества

в котором индексы служат лишь для установления различия элементов, а вовсе не для указания их взаимного расположения. В последнем случае в замаскированном виде было бы задано отношение следования, а я хочу указать все отношения явно. По-прежнему должны быть заданы отношения начала, конца и следования:

Кроме того, нужно было бы задать шесть унарных отношений, задающих вид букв. Обозначим для удобства эти отношения теми буквами, вид которых они задают:

Теперь слово "параметр" будет передано в виде алгебраической структуры (М', H', K', C', а, е, м, п, р, т).

Другие способы описания слов средствами абстрактной алгебры я приводить не стану. Они аналогичны рассмотренным. Неудобство всех этих способов не ограничивается их сложностью, которая читателю, надеюсь, ясна. Оказывается, что даже локальное изменение рассматриваемого слова вызывает очень значительные изменения в его алгебраическом описании. Это связано с тем, что все отношения заданы на основном множестве. Например, в последнем случае, отбрасывая первую букву, т. е. "т", мы не только исключим отношение "п" и, понятно, изменим множество М', а также отношение H', что естественно, но и изменим отношение следования С', хотя фактически оно осталось тем же самым, только проверять его для буквы "п" не нужно.

Из приведенного нами сравнения описания одних и тех же объектов средствами символьных конструкций и средствами абстрактной алгебры вовсе не следует, что абстрактная алгебра плоха. Просто в данном случае она неудобна. Менее абстрактный аппарат символьных конструкций лучше и проще передает свойства изучаемых нами объектов - носителей информации.