2.3. Алфавиты. Классы символьных конструкций

Для того чтобы ограничить число видов применяемых букв, обычно поступают следующим образом. Выбирают некоторое слово, все буквы которого попарно различны, и уславливаются никаких букв, кроме тех, которые одинаковы с буквами взятого слова, не применять. При этом указанное выше слово называют алфавитом (букв). Всякую букву, одинаковую с одной из букв алфавита, называют буквой в этом алфавите. Например, если

является алфавитом, то "б" - буква в А, а "р" - не является буквой в А. Слово, образованное из букв в А, называется словом в А.

Если бы мы ограничились конструкциями, являющимися словами, то описанный прием был бы для нас вполне достаточен, так как число видов связей следования ограничено (их три). Очень часто так и делают. Но для нашей цели слова как символьные конструкции слишком бедны. С их помощью без специальных ухищрений нельзя даже описать предложения естественного языка. Правда, ухищрения эти довольно примитивны. Нужно все буквы (прописные и строчные), а также знаки препинания и пробелы считать буквами. Тогда любой текст можно считать словом. Но в более сложных случаях такой прием уже недостаточен. Для каждого нового вида конструкций, чтобы их изобразить словами, приходится изобретать новый прием. Итак, нам нужно найти способ ограничивать число применяемых видов связей, но не ограничивать сложность конструкций.

Для этого можно рассматривать связи как буквы и задать их алфавит. Но это невозможно сделать в той области, в которой они являются связями. Однако ничего страшного в этом нет. Алфавит связей, как впрочем и алфавит букв, относится не к упомянутой области, а к области, в которой мы упомянутую область описываем, по существу, к области теории.

Итак, для ограничения числа видов применяемых букв и применяемых связей нужно задать два алфавита: букв и связей. Предполагается, что группировочная буква и группировочная связь в эти алфавиты не входит. Поэтому, если в рассматриваемом классе конструкций используются и оболочки, то задают еще однобуквенный алфавит оболочек. Если А - алфавит букв, В - алфавит связей, а ∑ - алфавит оболочек, то запись (А, В) означает класс конструкций, в котором используются буквы в А и связи в В. Запись (А, В, ∑) означает класс конструкций, в которых,кроме того,используются оболочки.

Если в рассматриваемой области (как, например, при традиционном представлении слов) связи изображаются не символами, а как-либо иначе, то при записи алфавита связей их можно как-нибудь обозначить, но обязательно иначе, чем буквы.

Алфавит характеризуется не только своим буквенным составом, но и порядком следования букв. Этот порядок называют алфавитным, или лексикографическим.

Алфавиты можно объединять и пересекать. Если А и С - два алфавита, то их главное пересечение получают так: просматривают алфавит А и выписывают только те его буквы, которые являются буквами в С. Получаемый при этом алфавит обозначают А∩С. В последнем алфавите можно переставлять буквы. При этом будут получаться другие (но уже не главные) пересечения алфавитов А и С. Главное объединение алфавитов А и С получим, приписывая к алфавиту А те буквы алфавита С, которые не являются буквами в А, сохраняя их порядок. Переставляя буквы в этом новом алфавите, получают другие (уже не главные) объединения алфавитов А и С. Главное объединение А и С обозначают A∪C.

Предположим, что

Тогда

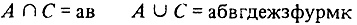
Заметим, что, пересекая два алфавита, мы можем получить результат, не содержащий ни одной буквы, т. е. пустой алфавит. Поэтому целесообразно Допустить существование пустого алфавита. Иначе при операциях над алфавитами результата могло бы не быть и такая возможность заставляла бы нас постоянно контролировать, не исчезает ли результат пересечения алфавитов. Это постоянно отвлекало бы внимание. Если А - пустой алфавит, то пишут А = ∅.