2.2. Точное определение символьной конструкции [1983 Криницкий Н.А.

Робот - устройство настолько сложное, что для отображения в нем картины внешней среды или картины действий эффекторов могут потребоваться очень сложные символьные конструкции. В связи с этим целесообразно привести полное математическое определение символьной конструкции, не ограничиваясь частными случаями или примерами. Для большей простоты мы разделим это определение на части. Предварительно скажем несколько слов об определении вообще.

Понятия математики можно разделить на две группы: первоначальные, или неопределяемые; производные, или определяемые. Первоначальные понятия должны быть очень подробно описаны и разъяснены. В современных дедуктивных математических дисциплинах первоначальные понятия должны быть выражены в аксиомах теории. У нас примерами неопределяемых понятий могут служить понятия буквы, связи, ветви связи. Производные понятия должны быть выражены через другие понятия, которые являются либо первоначальными, либо уже определены. Примером такого понятия служит оболочка.

Каким же образом определяют новые понятия? Общеизвестным видом является так называемое прямое определение. Например, можно сказать: "Пони - это порода лошади, рост которой не превосходит 100 см". Я не берусь утверждать, что мое определение совпадает с применяемым в коневодстве, но это - определение. Понятие "пони" определяется в нем через уже известные (или предполагаемые известными) понятия "порода лошади", "рост", "100", "см". Второй пример возьмем из геометрии. "Две прямые, лежащие в некоторой плоскости, называются параллельными, если они либо совпадают, либо не пересекаются". Здесь понятие "параллельность прямых" выражено через понятия "плоскость", "прямая", "лежать", совпадение", "пересечение".

Иногда допускают ошибку в прямом определении, заключающуюся в том, что в качестве одного из уже известных понятий берут понятие, которое само выражено через определяемое. Прямое определение при этом "замыкается", превращаясь в так называемый порочный круг. В математике порочные круги считаются недопустимыми. Порочный круг получился бы, если бы мы сказали: "Верблюд, имеющий два горба, называется двугорбым верблюдом. При этом верблюдами называются безгорбые верблюды, одногорбые верблюды и двугорбые верблюды". Это определение, по существу, содержит два более простых определения, которые вместе образуют порочный круг. Из такого определения нельзя узнать, ни что такое верблюд, ни что такое двугорбый верблюд.

Если вдуматься в логическую структуру приведенных определений, то можно заметить, что каждое определение называет новое понятие, приводит уже известные понятия и с помощью остальных своих слов формирует содержание нового понятия через уже известные. Можно представить себе, что каждое определение содержит оператор^*, перерабатывающий известные понятия в определяемое. В наших примерах такие операторы либо выделяли часть объема одного из известных понятий с помощью других понятий, либо объединяли объемы нескольких понятий. Например, в определении параллельных прямых из класса всех пар прямых плоскости, в которые входит данная прямая, сперва выделялись два подкласса: сливающихся прямых и непересекающихся прямых ("за бортом" оставались все пары пересекающихся, но не сливающихся прямых), а затем эти два подкласса объединялись. Таким образом, операторы определений не расширяли объем понятий.

Нужно отметить, что возможны операторы, которые расширяют объем понятий. Например, оператор определения "Строкой букв называется результат, который получится, если к строке букв приписать еще одну букву" является расширяющим. Правда, последнее определение - порочный круг, так что это расширение понятия все же ничего не дает. Но оказывается, что если такое циклическое определение дополнить удачно выбранным прямым определением, то получится вполне продуктивное определение. Например, можно было бы сказать: "Строкой букв называется 1) отдельная буква, а также 2) строка букв, к которой приписана еще одна буква". Это уже не порочный круг. Прямая часть определения позволяет задать некоторый начальный объем понятия "строка букв" (она задает все однобуквенные строки букв), а циклическая часть с помощью многократных повторений расширяет этот объем (включает в него сначала все двухбуквенные строки, потом все трехбуквенные и т. д.).

Определения такого вида, имеющие прямую часть и циклическую часть с расширяющим оператором, называются рекурсивными, или, точнее, определениями по индукции.

Сделав вышеприведенные разъяснения о структуре определений, мы можем теперь приступить к уточнению понятия символьной конструкции.

Определение 1. Конструктивным элементом называется или отдельная буква, или несколько конструктивных элементов, заключенных в оболочку, или произвольная конструкция, заключенная в оболочку.

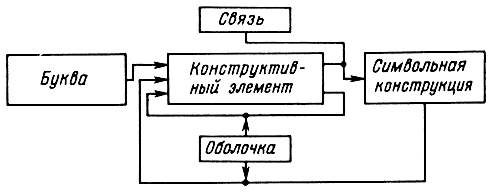
Рис. 2.4. Схема сложного рекурсивного определения понятия символьной конструкции

Это определение рекурсивно. Его прямая часть объявляет конструктивными элементами отдельные буквы. Циклических частей у него две: одна "короткая", объявляющая конструктивным элементом то, что получится, если несколько (отдельных) конструктивных элементов заключить в оболочку (рис. 2.4), а вторая - "длинная", содержащая в своем составе еще не приведенное определение символьной конструкции.

Определение 2. Связь называется насыщенной, если число связанных ею конструктивных элементов равно ее рангу.

Определение 3. Два конструктивных элемента, каждый из которых не внутренний для другого, называются непосредственно связанными, если существует связь, которая одной ветвью взаимодействует с одним из них (или с внутренним для него конструктивным элементом), а другой ветвью - с другим (или с внутренним для него конструктивным элементом).

Определение 4. Два конструктивных элемента называются связанными в одном из двух случаев:

Определение 4 является рекурсивным. Первая его часть говорит, что элементы связаны, если они являются непосредственно связанными, а вторая часть, циклическая, - что, кроме того, элементы связаны, если они являются первым и последним в цепочке непосредственно связанных элементов.

Определение 5. Конструкцией (точнее символьной конструкцией) называется или пустое множество, или отдельный конструктивный элемент, или совокупность нескольких конструктивных элементов, которой соответствует некоторое количество связей,причем каждая из указанных связей насыщена конструктивными элементами из названной совокупности и каждые два конструктивных элемента из названной совокупности связаны связями из числа указанных.

Теперь мы имеем полное и строгое определение символьной конструкции. Ранее описанные слова и последовательности слов являются частными видами конструкций.

В определении 5 мы указали один частный случай символьной конструкции: пустое множество. С этим случаем мы уже встречались, когда в § 2.1 говорили о пустых словах. Тем не менее сделаем некоторое разъяснение понятия "пустое множество". В математике множеством называется абстрактный предмет, являющийся совокупностью (коллекцией, собранием) других предметов, называемых элементами множества. Отношение между элементом множества и множеством обозначают символом ∈, так что запись а ∈ А означает "я является элементом множества А". Множества равны (одинаковы) , если они состоят из одних и тех же элементов. Примерами множеств являются стадо быков, куча камней, содержимое мешка гороха и т. п.

Если некоторые элементы множества А являются элементами множества В и других элементов множество В не содержит, то В называется подмножеством или частью множества А. При этом пишут В ⊆ А. Знак ⊆ обозначает отношение, существующее между частью и всем множеством. Для удобства вводят понятия одноэлементного множества и пустого множества. Первое состоит ровно из одного элемента, а второе не содержит ни одного элемента. Но пустое и одноэлементное множества не являются просто математическими соглашениями. Например, отбрасывая от множества по одному его элементу, мы после такой операции получаем новое множество. В конце концов, может быть, мы получим одноэлементное множество, а на следующем шагу и пустое. При этом нужно иметь в виду, что одноэлементное множество - это не то же, что его элемент, а про пустое множество нельзя говорить, что это "ничто". Пустое множество считается частью любого множества.

Следует обратить внимание на такую тонкость. Все элементы любого множества между собой различны и каждый из них хотя бы чем-нибудь отличается от любого другого элемента, принадлежащего тому же множеству. Это кажется удивительным только на первый взгляд. Ведь и в природе все предметы между-собой различны. Даже близнецы отличаются друг от друга хотя бы тем, что занимают разное место в пространстве. "Одинаковые" предметы тоже различны, они только в каком-то смысле похожи друг на друга.

На рис. 2.5 показаны примеры различных символьных конструкций.

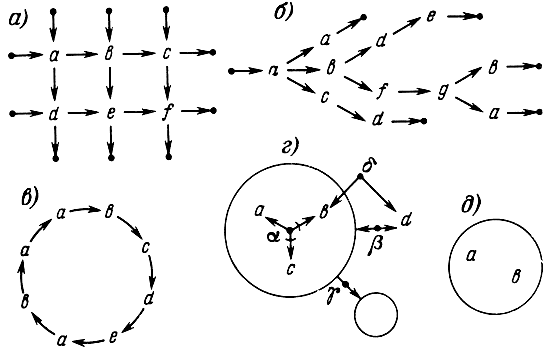
Рис 2.5. Простейшие символьные конструкции: а - матрица; б - дерево; в - кольцо; г - конструкция, содержащая две оболочки, одна из которых пустая, а другая неразделяющая (связь δ проникает сквозь нее); д - конструкция, содержащая в оболочке две несвязанные между мобой буквы

Если в некоторой символьной конструкции мы можем указать оболочку, такую, что ни одна связь не связывает конструктивные элементы, заключенные внутри нее, с конструктивными элементами, находящимися вне ее, то эту оболочку называют разделяющей. В противном случае (при наличии связей, проникающих сквозь оболочку) ее называют неразделяющей.

Из определения конструкции мы знаем, что внутри оболочки может заключаться либо некоторая (более простая) конструкция, либо несколько несвязанных между собой конструктивных элементов.

Если в составе конструкции К содержится разделяющая оболочка, заключающая в себе (группирующая) конструкцию К', то К' называется подконструкцией конструкции К. При этом пишут К'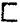

К, где знак

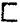читается "является подконструкцией" и обозначает отношение, существующее между подконструкцией и конструкцией. Мы видим из определения, что сама конструкция К своей подконструкцией не является. Конструктивный элемент может быть подконструкцией, если он один сгруппирован разделяющей оболочкой.