2.1. Буквы, связи, оболочки

Символ, который в данной области применения никогда не изменяется и никогда не подвергается делению на составные части, называется буквой. Реальные буквы, конечно, лишь приблизительно удовлетворяют этим условиям, но совершенно необходимо, чтобы имеющие место отступления были настолько малы, чтобы ими можно было пренебречь.

Считается, что каждую букву всегда опознают как букву, а не как сочетание букв или что-либо иное, и, кроме того, если даны две буквы, то всегда ясно: одинаковы они или различны. Это следует понимать так: элементы робота всегда различают, одинаковы или различны буквы.

При построении символьных конструкций буквы являются наиболее простыми конструктивными элементами.

Введенное нами понятие буквы - математическое. Оно абстрактно, так как не учитывает физической природы и даже геометрической формы букв. Нужно отметить, что оно не совпадает с понятием буквы, знакомым нам в обиходе. Приведем примеры.

Буквы русского алфавита являются буквами в нашем смысле, но знаки препинания с нашей точки зрения - тоже буквы. Десятичные цифры (часто называемые арабскими) являются буквами. Знак 7 и имеющий тот же смысл знак VII очень отличаются друг от друга: первый является буквой, а второй состоит из трех букв. В некоторых ЭВМ числа представляются в так называемой двоично-десятичной системе счисления. В ней каждая арабская цифра кодируется четверкой двоичных цифр (двоичных цифр две: 0 и 1). Так, °000 представляет собой арабскую цифру 0, а 0001 и 1001 - соответственно и 9. В области применения, которую можно назвать "двоично-десятичная арифметика", буквами являются указанные сочетания нулей и единиц. В области денежного обмена металлические монеты и бумажные купюры можно считать буквами. Каждая из них неделима и неизменяема. Мы видим, что понятие буквы тесно связано с областью применения. Переходя из той области, в которой данные знаки являются буквами, в другую область применения, мы уже будем, возможно, анализировать их составные части, преобразовывать их, но при этом следует не забывать, что в новой области они уже не буквы.

Невозможно указать абсолютные требования, которым должны удовлетворять символы для того, чтобы быть буквами, потому что таких требований нет. В § 2.2 я опишу один из приемов, с помощью которого можно задать требования, при выполнении которых буквы относятся к определенной области.

Второе важное понятие - связь. В отличие от букв связи не во всех областях применения задаются в виде символов, хотя в каждой из таких областей они тоже являются неделимыми и неизменными. Каждая связь, когда с ней приходится иметь дело, всегда распознается как связь. Любые две связи всегда воспринимаются как одинаковые или как различные, и это восприятие их в данной области применения неизменно. Но ни в какой области применения используемые там связи не выступают в роли конструктивных элементов! Таким образом, уже теперь мы видим различие между связями и буквами. Буквы в своих областях применения являются символами и конструктивными элементами. Связи не всегда являются символами и никогда не бывают конструктивными элементами. Они - тот "цемент", который "скрепляет" между собой буквы при образовании сложных конструкций.

Кроме описанных, связи обладают еще некоторыми свойствами, очень важными для нас. Каждая связь может связывать ("скреплять между собой") строго определенное число конструктивных элементов, называемое рангом связи. Для большей наглядности можно представлять себе, что взаимодействие связи и конструктивного элемента осуществляется посредством так называемой ветви связи. При этом число ветвей связи равно ее рангу. Наше математическое определение связи и ее ветвей абстрагируется от того конкретного (может быть, физического) способа, которым связь взаимодействует с конструктивным элементом, так что ветвь - это мысленная схема. На рисунках удобно связь изображать каким-либо значком, от которого в разные стороны идут отрезки линий, обозначающие ветви.

Считается, что вся совокупность ветвей связи разбита на группы, причем две ветви, принадлежащие одной и той же группе, называются одинаковыми (как говорят, имеющими одинаковый жанр), а принадлежащие разным группам - различными. Удобно пронумеровать группы ветвей связи с помощью неравных между собой целых положительных чисел, но не обязательно подряд. Это позволяет в качестве жанра ветви указывать номер группы, которой она принадлежит.

Характеристикой связи называется последовательность вида

в которой s - имя связи, а n_ij, - число ветвей жанра i_j. Символ j представляет собой так называемый "бегущий индекс", принимающий значения 1,2, ... Число к групп ветвей называется жанром связи.

Очень важно, чтобы в одной и той же области применения не использовались связи, имеющие одно и то же имя и неодинаковую последовательность чисел в остальной части характеристики (это приводит к путанице).

Чаще всего приходится встречаться со связями следования, которые бывают трех видов: начинающие (первого ранга), продолжающие (второго ранга и второго жанра) и заканчивающие (первого ранга). Эти связи можно проследить, анализируя слова, из которых составлены тексты, например на русском языке. Обозначим связи следования соответственно значкам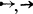и и 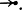Рассмотрим слово

В нем связи следования переданы не с помощью введенных нами значков, а с помощью особого расположения букв. Если бы мы явно указали связи, то получилось бы

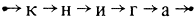
Начинающая связь связывает первую букву слова своей единственной ветвью (удобно считать, что жанр этой ветви 2). Каждая продолжающая связь связывает пару букв (одну - ветвью первого жанра, а другую, последующую, ветвью второго жанра). Заканчивающая связь связывает последнюю букву слова своей единственной ветвью, имеющей жанр 1.

Хотя в области книгопечатания связи следования в словах не указаны, но в их наличии (в том, что они подразумеваются) нас убеждает тот факт, что мы, не анализируя слова, находим его начало и конец, а взяв какую-либо букву слова (кроме последней), без труда находим следующую за ней. То обстоятельство, что связи следования в словах русского текста передаются именно особым расположением букв можно подтвердить, анализируя какое-либо слово, начертание букв которого не позволяет его ориентировать на листе. Например, слово "фон", если его напечатать "вверх ногами" превратится в "ноф", в котором все связи уже иначе связывают буквы.

Словом называется образованная из букв с помощью связей следования простейшая конструкция, в которой присутствует ровно одна начинающая ровно одна заканчивающая связь (и могут присутствовать несколько продолжающих связей). При этом каждая буква слова связана ровно двумя связями, из которых одна взаимодействует с ней ветвью второго жанра, а другая - ветвью первого жанра. В математике кроме того допускают слова, не содержащие ни одной буквы, а следовательно, и ни одной связи. Такие слова называют пустыми. Если хотят подчеркнуть, что слово содержит буквы (хотя бы одну), то его называют непустым.

Мы видим, что математическое понятие слова отличается от обиходного. Слово в математическом смысле - это особая символьная конструкция, а в обиходном смысле - элемент естественного языка, либо наделенный смыслом (знаменательное слово, например "стол", "стоит"), либо выполняющий какие-нибудь функции в предложении (незнаменательное слово, например "и", "как"). При этом, конечно, и в обиходном смысле слово является конструкцией из символов.

Приведем еще примеры связей. Нам нередко приходилось читать, что полицейский, задержав преступника, приковывает его к себе. При этом совершенно безразлично, какой "ветвью" он присоединит наручники к себе, а какой к преступнику. Наручники представляют собой связь, имеющую две одинаковые ветви (связь второго ранга и первого жанра). Иное дело, если бы мы имели наручники, которыми человека можно сковать со слоном. Здесь была бы связь второго ранга и второго жанра, ее ветви были бы различны. Связь третьего ранга и третьего жанра существует в семье, состоящей из мужа (отца), жены (матери) и ребенка. Эта связь уже не является графической, как в текстах, или физической. Она является моральной, юридической, социально-экономической, эмоциональной. В этой же семье существует и еще одна связь второго ранга и второго жанра между отцом и матерью как супругами.

Но конструктивные элементы могут быть более сложными, чем отдельные буквы. Рассмотрим например фразу

В ней два слова и неверно было бы утверждать, что слово "начата" следует за буквой "а" или за пробелом. Это слово следует за словом "книга", и оба слова при этом играют роль конструктивных элементов. Вводя связи следования нового вида, мы могла бы написать

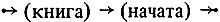
где скобки показывают, что каждое слово при построении фразы используется как целое, как бы заключено в "прозрачную" оболочку.

В обычном тексте связь, начинающая фразу, передается тем, что первая буква первого слова является прописной, продолжающая связь передается пробелом, а заканчивающая фразу связь выражена точкой (т. е. графическим знаком). В более сложных текстах используется еще ряд связей и в оболочки могут быть заключены не только слова, но и целые фразы (при этом оболочки оказываются вложенными друг в друга). В последнем примере мы приходим к новому понятию, к понятию оболочки. Однако, оказывается, что оболочку можно представить с помощью букв и связей.

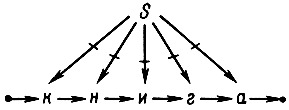
Рис. 2.1. Сгруппированная конструкция

Введем специальную букву, которую назовем группировочной и для иных целей использовать не будем, и особый вид связей - группировочных, имеющих второй ранг и второй жанр. Группировка конструктивных элементов будет заключаться в том, что мы будем их связывать группировочными связями с группировочной буквой. При этом будем следить за тем, чтобы группируемые конструктивные элементы взаимодействовали с ветвями второго жанра группировочных связей, а группировочная буква - с их ветвями первого жанра (рис. 2.1).

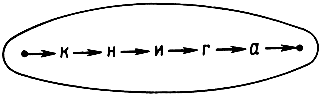
Рис. 2.2. Конструкция, заключенная в оболочку

Оболочкой называется совокупность группировочной буквы и соответствующего числа взаимодействующих с ней группировочных связей. На схемах оболочку будем часто изображать в виде замкнутой линии, окружающей заключенные в нее конструктивные элементы (рис. 2.2).

Если связь (ранга r) связывает конструктивные элементы, которые все заключены в некоторую оболочку, то будем считать, что она тоже находится внутри этой оболочки. Если все конструктивные элементы, связанные некоторой связью, находятся вне оболочки, то и связь считается находящейся вне оболочки. Наконец, если часть конструктивных элементов, связанных связью, находится внутри оболочки, а другая часть вне нее, то связь считается пронизывающей оболочку. Все эти детали мы описываем так подробно потому, что, хотя на схемах оболочка изображается непрерывной замкнутой линией, в действительности она непрерывной не является.

Рис. 2.3. Фактическая связь конструкций, заключенных в оболочки

Наконец,отметим, что если конструктивным элементом является нечто, заключенное в оболочку, то фактически соответствующая ветвь связи, взаимодействующая с этим конструктивным элементом, взаимодействует с группировочной буквой упомянутой оболочки (рис. 2.3).

Таким образом, символьные конструкции в своем составе могут иметь элементы трех видов: буквы, связи, оболочки.