4.6. Терминология и правила записи

Для первичных алгоритмов - правило выполнения, а для "=n-арных - алгоритм выполнения определяют отвечающие им процессы преобразования исходных данных в искомые результаты. Эти процессы называют алгоритмическими. Каждой паре "алгоритм - операнд" отвечает алгоритмический процесс. При этом возможен один из трех случаев:

1. алгоритмический процесс заканчивается получением искомого результата;
2. алгоритмический процесс безрезультатно обрывается;
3. алгоритмический процесс никогда не заканчивается.

Все эти случаи мы можем наблюдать уже на первичных алгоритмах. Например, составленный на с. 66 алгоритм нахождения конца слова приводит к результативному окончанию процесса для любого операнда, являющегося непустым словом. Этот же алгоритм безрезультатно остановится на первом же приказе, если его применить к квазислову. Это связано с тем, что логическая операция "проверка непустоты" имеет смысл только для слов, а не для квазислов. Наконец, тот же алгоритм порождает процесс, который никогда не закончится, если его применить к пустому слову.

В первом из вышеперечисленных случаев говорят, что алгоритм применим к своему исходному данному; во втором и третьем случаях - что алгоритм неприменим к нему. Применимость или неприменимость алгоритма рассматривается только по отношению к предложениям языка его исходных данных.

Два алгоритма, имеющие один и тот же язык исходных данных, называются функционально эквивалентными, если одни и те же исходные данные они преобразуют в одни и те же результаты. Ясно, что если один из двух функционально эквивалентных алгоритмов неприменим к какому-нибудь операнду, то и второй тоже неприменим к этому операнду.

Функционально эквивалентные алгоритмы могут, однако, для одного и того же исходного данного порождать различные алгоритмические процессы. Из этого вытекает интересное следствие. Предположим, что функционально эквивалентны два алгоритма выполнения. Тогда очевидно, что порождаемые ими семейства алгоритмов между собой совпадают в том смысле, что одинаковые записи алгоритмов этих семейств являются записями функционально эквивалентных алгоритмов. Однако порождаемые ими процессы преобразования могут быть различны.

Таким образом, по записи алгоритма нельзя судить о том, какой алгоритмический процесс он порождает. Это очень важный факт, объясняющий, почему нельзя строить теорию алгоритмов, отправляясь от алгоритмического процесса.

Мы уже знаем и уже пользовались этим обстоятельством, что каждый алгоритм осуществляет некоторое отображение или, как говорят, индуцирует некоторую функцию.

С точки зрения математической лингвистики алгоритм - это наделенное смыслом предложение формального языка. С точки зрения абстрактной алгебры он - совокупность элемента множества символьных конструкций и функции, соответствующей алгоритму выполнения.

Наша точка зрения - это точка зрения математической лингвистики с тем ее уточнением, что семантику алгоритмическому языку придает именно алгоритм выполнения.

Так как записи алгоритмов могут быть операндами для других алгоритмов, то следует различать сам алгоритм, его запись и индуцируемую им функцию. Условимся алгоритмы обозначать прописными латинскими буквами, их записи - теми же буквами с чертой над ними, индуцируемые ими функции - теми же буквами с волной.

Эти предосторожности в обозначениях позволят нам пользоваться обычной символикой, разработанной в математике для записи формул, содержащих функциональные знаки. Для того чтобы не делать различия между операндами и записями алгоритмов, если они оказываются операндами, условимся предложения языков исходных данных впредь считать записями операндов, что вполне логично, так как при решении задач операндами являются не сами записи, а записи, наделенные смыслом. Записи операндов также будем обозначать буквами с чертой сверху.

При соблюдении указанных правил записи формул циклическую часть определения алгоритма "-го ранга можно записать в следующем виде.

Если 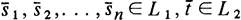и W - алгоритм, определяющий функцию 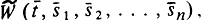то t является алгоритмом, и, коль скор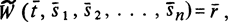о, то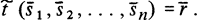

При написании этих формул связи z и z' отражать в записи не нужно, потому что они фиксированы для всех возможных значений аргументов и, следовательно, в неявном виде учитываются в символах 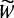и .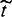

Если при построении двух семейств n-арных алгоритмов для образования промежуточных формальных языков были в одном случае употреблены связи z и z', а в другом - связи ς и ς', и если, заменяя z на ς и z' на ς' (или обратно), мы превращаем одно семейство алгоритмов в другое, то эти семейства называются одинаковыми с точностью до технических деталей.

В заключение данного параграфа приведем без доказательства очень важную теорему: для любого семейства первичных алгоритмов на достаточно высоком уровне семейств алгоритмов существует алгоритм выполнения, эквивалентный правилу их выполнения.

Эта теорема хотя и не снимает необходимости в правилах выполнения при определении понятия первичных алгоритмов, но делает их вполне равноправными со всеми другими алгоритмами и дает возможность не доказывать отдельно теоремы для первичных и для n-арных алгоритмов. Кроме того, она позволяет первичные алгоритмы отнести к 1-арным алгоритмам и впредь говорить об "арности" алгоритмов лишь тогда, когда она имеет существенное значение.