4.7. Операторные алгоритмы

В функциональном анализе, одном из основных разделов современной математики, операторами называют функции, значения которых, а также значения аргументов которых могут быть объектами нечисловой природы. В силу этого определения функции, индуцируемые алгоритмами, являются операторами (так как значения их самих и их аргументов - символьные конструкции). Дальнейшее изложение я буду вести применительно к алгоритмам, используя правила записи формул, введенные выше (на с. 70).

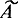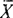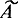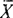Пусть - некоторый оператор, а - его исходное данное (операнд). Результат применения оператора к обычно обозначают 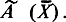Если 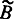- второй оператор и результат выполнения первого может быть его операндом, то 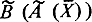по определению оператора - тоже оператор. Бифункциональном анализе для него введено специальное обозначение 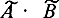и название - произведение оператора 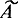на оператор .

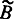Пусть теперь 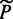- некоторое условие, которому может удовлетворять или не удовлетворять (в зависимости от значения 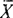) результат выполнения оператора 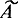. Очевидно, если выполнить 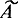, затем проверить условие 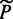, а далее применить оператор 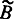, если условие выполнено, или оператор 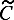, если оно не выполнено, то такая композиция операторов и условия тоже будет оператором. Запишем ее так:

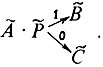
Сами операторы 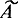, 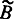и 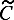могут в свою очередь быть произведениями или композициями, и тогда операторное выражение усложняется. В некоторых случаях после проверки условия, при одном из ее исходов нужно повторить выполнение оператора, результат которого проверялся; при этом возможны операторные выражения вида

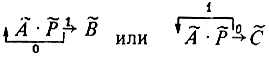
Еще в 1953 г. А. А. Ляпунов, основоположник советской школы программирования, заметил, что большое число методов решения задач (практически все) можно схематически описать с помощью операторных выражений указанного выше типа. Если бы оказалось, что операторы соответствуют практически удобным алгоритмам и существует простой прием, позволяющий после выполнения одного из алгоритмов переходить к выполнению другого, используя результат первого как операнд второго, то операторные выражения стали бы важным средством для облегчения работ по составлению сложных алгоритмов. А. А. Ляпунов заметил, что программы для ЭВМ являются именно такими алгоритмами. Читатель увидит несколько позже, что программы ЭВМ образуют семейства алгоритмов, для которых сами ЭВМ являются физическими реализациями алгоритмов выполнения.

Все это привело А. А. Ляпунова к идее логической схемы алгоритма, получающейся из операторного выражения, если в нем функции заменить символами, обозначающими имена алгоритмов, а знаки умножения операторов и стрелки толковать как знаки перехода от одних алгоритмов к другим. Логическая схема алгоритма передает одновременно и структуру алгоритма и его "смысл" (если известен смысл каждого оператора). При построении логических схем оказалось целесообразным обозначать конец выполнения алгоритма и его "вход", т. е. "место", с которого начинается процесс его выполнения. Для этого были введены стандартные символы И_О и Я, получившие названия операторов начала и конца. Алгоритмы, включенные в логическую схему, стали называть ее операторами. Метод программирования, основанный на идее логической схемы, получил название операторного метода. Семейства алгоритмов, допускающих описания алгоритмов в виде логических схем, отражающих не только их содержание, но и структуру, называют семействами операторных алгоритмов.

Любое семейство первичных алгоритмов, объединенное его алгоритмом (или правилом) выполнения, является, семейством операторных алгоритмов. Покажем это.

Выполнение первичного алгоритма всегда начинается с приказа, стоящего в его записи на первом месте. Этот приказ будем называть входом первичного алгоритма. После выполнения операции, названной в безусловном приказе, производится переход к первому, если идти от начала записи алгоритма, приказу, имеющему метку, одинаковую с отсылкой только что выполненного приказа. Заметим, что в записи первичного алгоритма может быть несколько приказов с одинаковыми метками, но, как следует из правила выполнения, выполняться может только тот из них, который расположен ближе к началу записи. (Это замечание не имеет, правда, непосредственного же к началу записи. (Это замечание не имеет, правда, непосредственного отношения к вопросу, который мы в данный момент исследуем, но несколько ниже оно нам потребуется).

После выполнения логической операции, на которой указан в условном приказе, выбирается одна из двух отсылок, а затем переход производится так же, как и в случае безусловного приказа. Мы видим, что операции-преобразования можно рассматривать как операторы, а логические операции как условия. Пары "отсылка - метка", если они одинаковы, можно рассматривать как переходы (с учетом выше сделанного замечания о способе перехода). При этом отсылки типа <стоп > являются операторами конца, а перед входом алгоритма подразумевается оператор начала. Таким образом, каждый первичный алгоритм можно рассматривать как операторное выражение и представлять в виде логической схемы. Для примера алгоритм проверки, является ли операнд словом или квазисловом, который приведен на с. 67, изображен в виде логической схемы на рис. 4.1.

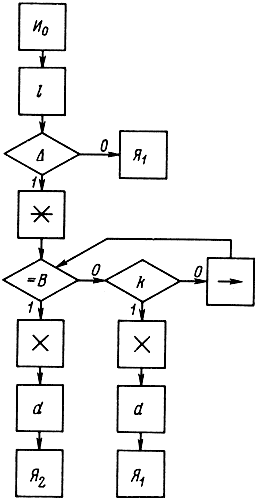
Рис. 4.1. Логическая схема первичного алгоритма: Квадратами изображены операторы, ромбами - условия, стрелками - переходы. Цифра 0 означает переход в случае невыполнения условия, а цифра 1 - в случае его выполнения

Операции являются наиболее элементарными (наиболее "мелкими") операторами и условиями, возможными для данного семейства первичных алгоритмов. Своими рассуждениями мы, по существу, доказали теорему о том, что любой первичный алгоритм можно представить в виде логической схемы. Но этого мало. Нужно еще доказать, что, имея несколько алгоритмов и условий, всегда можно из них образовать произведения операторов и композиции.

Заметим прежде всего, что если все одинаковые между собой отсылки и метки, присутствующие в записи первичного алгоритма, заменить одинаковыми словами (т. е. одним и тем же словом), удовлетворяющим метаформуле, в левой части которой стоит метасимвол <метка>, и отличающимися от всех других меток и отсылок записи алгоритма, то получится запись нового первичного алгоритма того же семейства, эквивалентного исходному. Это следует из правила выполнения. Например, если в записи алгоритма, различающего, является ли операнд словом или квазисловом (с. 67), все отсылки и метку, имеющие вид "4", заменить допустимым словом "100", то получится

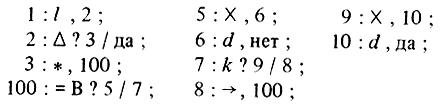
Это - запись алгоритма, эквивалентного исходному и даже имеющего с ним одну и ту же логическую схему.

Теперь легко сообразить, как после выполнения какого-нибудь алгоритма обеспечить выполнение другого, если они принадлежат одному и тому же семейству и записи обоих заданы. Нужно все отсылки и метки второго с помощью допустимых замен сделать отличающимися от отсылок и меток первого (это не относится к отсылкам типа <стоп>). Затем необходимо вместо соответствующего выхода из первого алгоритма (т. е. вместо всех одинаковых между собой отсылок типа <стоп>) поставить отсылки, равные метке первого приказа второй записи. Иногда, но это уже зависит от содержания задачи, производят замену отсылок типа <стоп> другими отсылками этого же типа.

Пример 4.1. Если бы нам нужно было, распознав, является ли операнд словом или квазисловом, в первом случае оставить операнд неизменным, а во втором - приписать к его концу букву а и сделать словом, то можно было бы воспользоваться вышеприведенным алгоритмом распознавания, который играл бы роль условия, и алгоритмом

1. k ? 2 / 4 ;
2. ↑ a, 3 ;
3. ×, стоп ;
4. →, 1 ;

Обозначая условие через Р, а последний алгоритм через А, мы можем запись искомого алгоритма строить по логической схеме

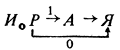
Для этого:

1. в записи последнего алгоритма произведем изменение отсылок и меток, увеличивая (если рассматривать их как целые числа) на 10;
2. отсылку "нет" условия заменим отсылкой "11"; этим мы свяжем два алгоритма в один;
3. отсылку "да" условия заменим отсылкой "стоп". Запись искомого алгоритма будет иметь вид:
   
   

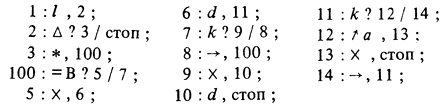
Понятие "операторные алгоритмы" охватывает бесконечное множество семейств алгоритмов, но известны семейства алгоритмов, которые не являются операторными. Например, не являются операторными известные нормальные алгоритмы А. А. Маркова [10].