8.2. Классификация коллективов роботов

В основу всякой классификации обычно кладут какой-либо признак или совокупность признаков, которыми может обладать или не обладать объект из классифицируемого класса объектов. Признак может быть двоичным (отсутствует - присутствует) или многозначным. В некоторых случаях классы, полученные по одному какому-то признаку, дальше разбивают на подклассы по другому признаку. При этом, если каждый класс изобразить точкой (или прямоугольником, в котором записано название класса), которую назовем вершиной, и между ними провести отрезки, ведущие от каждого класса к его подклассам, то возникает разветвляющаяся структура, называемая одноаспектным классификатором. С математической точки зрения такая структура представляет собой ориентированный граф, имеющий форму дерева (для наглядности добавим - обращенного ветвями вниз). Основанием этого дерева является совокупность всех классифицируемых объектов.

Если произведено несколько одноаспектных классификаций и все одноаспектные классификаторы объединены и при этом одноименные вершины (если такие имеются) совмещены, то получается так называемый многоаспектный классификатор. Входящие в его состав отрезки во избежание неясности следует пометить именем или номером аспекта.

Классифицируя коллективы роботов, мы должны исходить из таких признаков (свойств), которые не являются свойствами роботов, характеризуя именно коллективы их. Таких свойств мы знаем два: 1) характер связей между роботами - членами коллектива и 2) структура коллектива.

Условимся не считать запрос, пересылаемый из одного робота в другой, управляющей информацией, хотя вполне допустимо считать, что запрос - это приказ о выдаче ответа или другого приказа. Кроме того, введем понятие подколлектива. Под коллективом мы будем считать совокупность роботов, входящих в состав некоторого коллектива роботов, и являющуюся коллективом. При этом уточним один вопрос, касающийся коллектива роботов и не освещенный нами до сих пор.

Спрашивается, могут ли элементы коллектива роботов быть связанными с другими роботами, не принадлежащими данному коллективу? В отношении пассивных связей ответ на этот вопрос ясен: могут, потому что всякий робот находится в собственной внешней среде, независимо от того, что влияет на нее. Что же касается активных связей, то проблема сложнее. Если допустить и активные связи, то не получится ли, что любая часть коллектива роботов является педколлективом? С другой стороны, требование отсутствия внешних активных связей явно нецелесообразно, потому что оно привело бы к запрещению связей между коллективами. Но это противоречило бы нашим представлениям о роботах и их коллективах и не позволило бы также отдельный робот считать частным случаем коллектива (одноэлементным коллективом). Ясно, что мы не можем пойти на исключение возможности активных внешних связей. Однако никаких трудностей это не повлечет, так как основной признак коллектива - наличие коллективной функции - всегда позволит нам подколлектив отличить от всякой иной части коллектива.

После сделанных выше замечаний мы можем привести классификацию коллективов роботов по видам связей, которые в них существуют (рис. 8.1).

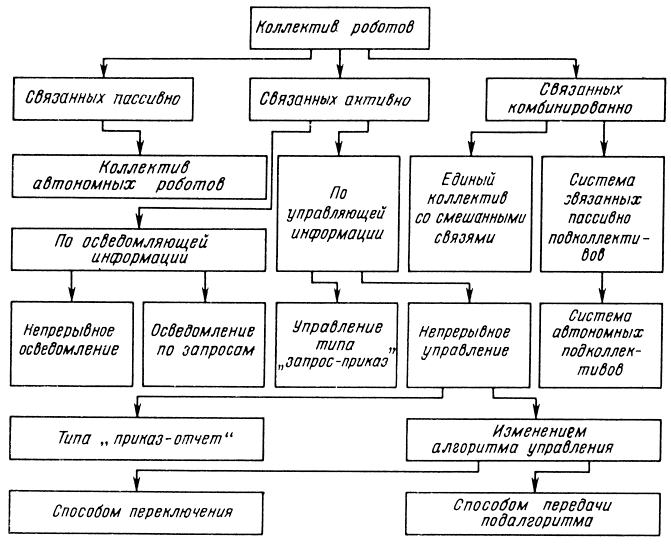
Рис. 8.1. Классификация коллективов роботов по видам связи между роботами

Недостатком этой классификации является то, что некоторые коллективы роботов могут попасть сразу в несколько классов. Например, если некоторые роботы активно связаны по осведомлению, а другие в том же коллективе активно связаны по управлению. Правда, в таком случае можно считать, что данный коллектив не попадает ни в один класс. Признаюсь, что ради экономии места и терпения читателя я просто опустил в классификаторе ряд "комбинированных" подклассов.

Автономные педколлективы, сами будучи коллективами, должны попасть в один из разделов классификаторов.

Скажем теперь несколько слов о втором возможном аспекте классификации коллективом роботов, связанном с их структурой. Структуру коллектива роботов нам поможет описать теория графов. Придется привести более подробные сведения из этой теории.

Справка из теории графов. Множество точек (назовем их вершинами) и множество ориентированных отрезков линий (назовем их дугами), соединяющих некоторые из этих точек, исходящих из них или входящих в них, называются в своей совокупности ориентированным графом. Две дуги, имеющие одно и то же начало и один и тот же конец, считаются одной и той же дугой и потому на схеме графа дважды не изображаются. Дуги, не имеющие начала, называются входами в граф, а не имеющие конца - выходами из графа. Если начало дуги и ее конец совпадают, то дуга называется петлей.

Если дуги какого-нибудь ориентированного графа пометить какими-либо значками, а затем провести новые дуги и тоже пометить их, следя за тем, чтобы дуги, имеющие одинаковые начала и одинаковые концы, отличались двоими пометками (такую операцию можно проделать многократно), то получится так называемый ориентированный размеченный мультиграф.

В дальнейшем слова "ориентированный" и "размеченный" мы будем опускать, так как неориентированные и неразмеченные графы и мультиграфы у "нас не будут встречаться.

Графы и мультиграфы называются связными, если из какой-либо их вершины можно прийти в любую другую вершину, двигаясь по дугам (без учета их направлений и пометок). В противном случае они называются несвязными.

Структуру коллектива роботов мы будем изображать в виде мультиграфа, вершины которого соответствуют роботам, являющимся членами коллектива, а дуги - связям между ними. В данной книге мы ограничимся тремя видами связей, а следовательно и тремя видами пометок на ребрах. Для того чтобы сделать структурные схемы коллективов более наглядными, вместо того, чтобы помечать дуги, будем изображать их пунктиром (пассивные связи) , тонкими линиями (связи по осведомляющей информации) и толстыми линиями (активные связи управления). При необходимости можно учитывать большее число видов связей; тогда мультиграф будет сложнее.

Классификацию структур коллективов роботов можно осуществить как классификацию соответствующих им мультиграфов.

Рис. 8.2. Структура одноэлементного коллектива роботов (одиночного робота)

Рассмотрим некоторые структуры коллективов роботов. На рис. 8.2 приведена структура одноэлементного коллектива, который состоит из одного робота. На этой схеме имеется один вход в мультиграф (воздействие на него внешней среды), один выход (воздействие робота на внешнюю среду) и одна петля (обратная связь). Если имеется робот, управляемый человеком-оператором, то его схема как одноэлементного коллектива будет иметь вид, показанный на рис. 8.3.

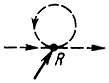
Рис. 8.3. Структура одноэлементного коллектива роботов, управляемого человеком

На рис. 8.4 приведена структура двухэлементного коллектива роботов, описанного в примере 8.2.

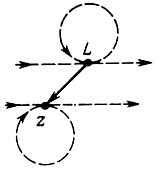
Рис. 8.4. Структура двухэлементного коллектива роботов, описанного в примере 8.2

Рассмотрим некоторые частные случаи коллективов роботов, которые мне кажутся интересными.