4. Логические алгоритмы планирования

Содержание задачи планирования поведения робота поясним на примере того, как эту задачу решает человек. Первое, с чем мы сталкиваемся ежедневно, - это задача утреннего одевания. Мы должны выбрать план действий, который позволит нам одеться, причем так, чтобы выполнялись естественные общепринятые ограничения (рубашку надевать необходимо, но не поверх пиджака, и т. п.). При этом время - наш основной ресурс, и выбранный план должен быть наилучшим в том смысле, в каком каждый понимает расход своего утреннего времени.

Если отбросить некоторые "несущественные" детали, план одевания должен оперировать такими предметами, как туфли, носки, брюки, рубашка, галстук, пиджак и пальто. План действий представляет собой любой порядок, в котором можно надеть эти предметы. Всего в этом случае существует 7! = 5040 различных вариантов плана. Многие из них недопустимы, так как либо не удовлетворяют общепринятым ограничениям (рубашка поверх пиджака, носки поверх ботинок), либо непрактичны (галстук под рубашкой). Но даже после того, как эти недопустимые решения будут отброшены, все равно придется исследовать некоторое количество допустимых планов. Как же выбрать окончательный (желательно, оптимальный) план? Прежде всего заметим, что в рассматриваемой задаче имеется некоторая мера эффективности, некий критерий, позволяющий нам сравнивать эффективность допустимых планов. Если мы можем каким-то образом сравнить значение этого критерия для различных планов, то мы сможем тем самым выбрать из них оптимальный. В данной конкретной задаче естественно минимизировать время, необходимое для того, чтобы одеться. Это и есть та мера эффективности, с помощью которой можно сравнивать допустимые планы. Тогда в качестве оптимального плана, позволяющего одеться, не нарушая общепринятых ограничений, можно выбрать следующий план: носки, рубашка, брюки, галстук, туфли, пиджак, пальто. Ясно, что при другом критерии эффективности поведения оптимальным может оказаться иной план.

Характерной особенностью задач планирования является наличие многих допустимых решений. После того, как эти решения найдены, возникает следующая задача: выбрать среди них по крайней мере один оптимальный (в смысле определенного критерия) план.

В рассмотренном нами простейшем примере решения принимались без специальных обоснований, просто на основе опыта и здравого смысла. Оптимизация таких решений происходит как бы сама собой, в процессе жизненной практики. Если порой выбранный план поведения окажется не самым удачным, так что же? На ошибках учатся^*.

^* (Нередки, правда, ситуации (соответствующие, например, планированию мероприятий, осуществляемых в первый раз), когда использовать эвристические решения, основанные на опыте и здравом смысле, просто невозможно. В подобного рода ситуациях "опыт" молчит, а "здравый смысл" легко может обмануть, если не будет опираться на математический расчет.)

Но бывают решения несравненно более сложные, а главное ответственные - от них очень многое зависит. Конечно, при планировании поведения в подобного рода ситуациях можно действовать интуитивно, опираясь опять-таки на опыт и здравый смысл. Но гораздо более разумными могут оказаться решения, подкрепленные количественными, математическими расчетами соответствующего плана действий. Эти предварительные расчеты помогут избежать длительного и накладного поиска решения "на ощупь".

"Семь раз примерь, один раз отрежь", - говорит известная поговорка. Планирование поведения как раз и представляет собой своеобразное математическое "примеривание" к потребному будущему, позволяющее заранее оценить последствия каждого решения, заранее отбросить недопустимые планы и рекомендовать наиболее удачные. Эти последние позволят установить, достаточна ли имеющаяся у нас информация для правильного выбора решения, и если нет - какую информацию нужно дополнительно получать и обрабатывать. Все это позволяет при реализации плана экономить время, энергию и материальные средства.

Необходимость в планировании поведения возникает у робота при выполнении им сложных заданий в условиях большой априорной неопределенности (например, сборка сложного изделия по чертежу, поиск и транспортировка нужного объекта на неизвестной местности с препятствиями и т. п.). Задача автоматического планирования поведения, решаемая на втором уровне иерархии системы управления робота, может быть переформулирована на языке исчисления предикатов как задача логического вывода (автоматического доказательства теорем). При таком подходе априорные сведения о свойствах и функциональных возможностях робота и окружающей его среды необходимо прежде всего представить в виде правильно построенных формул (ППФ). Совокупность таких ППФ мы будем называть априорными аксиомами и разобьем их на четыре класса:

1) сенсорные аксиомы (СА);

2) моторные аксиомы (МА);

3) аксиомы среды (АС);

4) аксиомы начальных условий (АНУ).

Сенсорные аксиомы описывают функциональные возможности информационно-измерительной системы робота, а моторные аксиомы - функциональные возможности исполнительных механизмов робота. Аксиомы среды определяют состояние и эволюцию среды, а аксиомы начальных условий описывают начальные состояния робота и среды. В табл. 3 и 4 приведены типичные для задачи планирования поведения робота на местности с препятствиями термы, функции, предикаты и априорные аксиомы вместе с их интерпретацией на обычном (русском) языке.

Таблица 3

Таблица 4

Наряду с априорными аксиомами введем аксиомы обучения (АО), автоматически формируемые по мере накопления роботом опыта и знаний в процессе выполнения тех или иных заданий. Задания роботу, формулируемые человеком, будем трактовать как заключения теорем, посылками которых служат априорные аксиомы и аксиомы обучения. Заметим, что выбор аксиом и теорем диктуется окружающим робота миром, который он воспринимает своими органами чувств и на который воздействует своими исполнительными механизмами, а также структурно-функциональными особенностями робота и целями (задачами) его функционирования.

Для автоматического доказательства теорем-заданий и извлечения ответа на языке робота целесообразно применить адаптивную систему логического вывода, описанную выше. Такая система в результате доказательства теоремы-задания (или теоремы-вопроса) укажет, какие действия и в какой последовательности нужно роботу совершить для выполнения задания, т. е. выдаст искомый план поведения робота.

Продемонстрируем работу адаптивной системы логического вывода в задаче планирования поведения робота на примере. Пусть робот находится в цехе с оборудованием (трактуемом как препятствия), где имеются склад заготовок С₁ и склад готовых изделий С₂ (см. рис. 11). Вначале робот находится в точке О и перед ним ставится задача: перевезти определенный объект (который еще нужно распознать) со склада С₁ на склад С₂ (местоположение складов известно) и после этого покинуть цех через выход. Предполагается, что выход задан набором признаков (его координаты роботу неизвестны), а сенсорная система может измерять значения признаков и координаты видимых ею точек, причем она не может "видеть" сквозь препятствия. Кроме перечисленного и исходной системы аксиом, представленной в табл. 4, роботу ничего неизвестно.

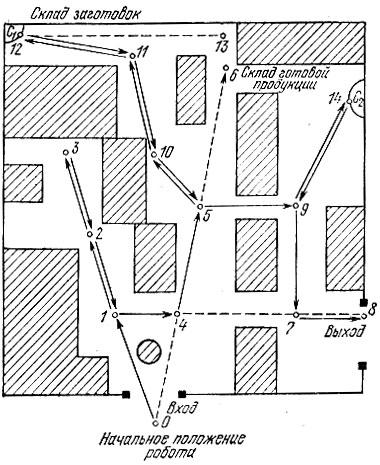
Рис. 11. Планирование поведения робота в незнакомом помещении

Поскольку решение этой задачи требует дополнительной информации об обстановке в цехе, робот вначале опрашивает сенсорную систему. При этом отыскиваются все видимые границы препятствий и около них фиксируются некоторые точки 1÷6, к которым робот может проехать по прямой. В результате автоматически строятся аксиомы среды: G(0, 1), G(1, 2), G(2, 3), G(0, 4), G(4, 5), G(5, 6). По этим данным, а также по аксиоме начальных условий Pos(s₀, О, C₁) робот пытается доказать теорему-задание ∃s Pos(s, fin, fin) (где s-переменная, описывающая ситуацию). Однако, поскольку знаний о среде, заключенных в построенных АС, явно недостаточно (теорема не выводима из АС), ответ, т. е. искомый план поведения, не будет получен. В процессе логического вывода робот убеждается, что маршруты через точки 0, 1, 2, 3 и 0, 4, 5, 6 к выполнению задания не приводят. Далее, используя критерий близости к складу С₁, робот принимает решение переместиться в точку 3. Последовательность действий на этом этапе определяется термом ситуации в резольвенте f(2, 3, f(1, 2, f(0, 1, s₀))), который расшифровывается в обратном порядке и в соответствии с определением функции f означает: переехать из точки 0 в точку 1, затем в точки 2 и 3. Передвигаясь согласно выбранному маршруту, робот останавливается в каждой из них и пополняет свои знания о среде посредством опроса сенсорной системы. Так возникают новые аксиомы среды (AC): G(1, 4), G(4, 7), G(7, 8), ¯|Pos(s, 8, y) ∨ Pos(s, fin, y) (последняя аксиома среды означает, что точка 8 находится у выхода).

Приехав в точку 3, робот не формирует ни одной новой АС, а поэтому и новой резольвенты. Он в тупике. "Осознав" это, робот вынужден развернуться и исправить те действия, которые привели его в "тупиковую" точку 3, в обратном порядке, пока не появится первая возможность образования новой резольвенты. В результате он выбирает маршрут через точки 1, 4, 5, используя ранее построенные аксиомы обучения (АО) (к числу которых относятся АС и СА, формируемые в процессе функционирования робота). Так, формируя и корректируя локальные планы поведения на основе целенаправленной переработки новой информации, робот, в конце концов, решает поставленную задачу: отыскивает (распознает) нужный объект на складе C₁, погружает (с помощью манипулятора) его на тележку, подвозит к складу С₂, сгружает объект и покидает цех через выход. При этом адаптивная система логического вывода строит 47 резольвент. Окончательный маршрут робота, реализующий выработанный план поведения, изображен на рис. 11 сплошными линиями со стрелками.

Рассмотренный пример планирования поведения робота в условиях большой априорной (начальной) неопределенности замечателен тем, что он ясно демонстрирует, что обычная (неадаптивная) система логического вывода принципиально не способна решать такого рода задачи без использования элементов обучения и адаптации. Важно отметить, что автоматическое формирование АО и адаптивная подстройка стратегии, использующей АО, не только делает задачу разрешимой, но и существенно сокращает (за счет отсечения многих тупиковых ветвей на дереве вывода) число шагов в процессе поиска плана поведения как при полной, так и при частичной информированности об условиях функционирования робота.