5. Алгоритмы распознавания ситуаций

Задача описания, распознавания и анализа ситуаций, решаемая на третьем уровне иерархии, является одной из центральных проблем построения интеллекта роботов. Для формализации и автоматизации решения этой задачи, как мы увидим ниже, опять-таки удобно использовать язык исчисления предикатов и адаптивную систему логического вывода. Поскольку для робота наиболее важное значение имеет зрительная информация, мы сосредоточим внимание на методах описания, распознавания и анализа трехмерных сцен по их изображениям. Что же касается задач переработки речевой, тактильной и другой сенсорной информации, то они могут решаться по существу теми же методами.

Трудности, возникающие при решении задачи распознавания отдельных предметов на сложной сцене, связаны с наличием "порочного круга": для того чтобы распознать некоторый предмет на сцене, нужно прежде всего его "выделить", а для того чтобы "выделить" этот предмет, нужно его распознать. Это приводит к тому, что классические методы распознавания "перцептронного" или статистического типа, кратко охарактеризованные в предыдущей главе, в этой задаче практически не применимы. На первый взгляд кажется, что выход из указанного "порочного круга" только один - полный перебор элементов изображения предмета и сцены. Однако более глубокий анализ этой задачи позволяет ее сформулировать и решить как задачу логического вывода.

Идея предлагаемого решения основана, во-первых, на том, что применяется предварительное обучение робота путем показа ему отдельных предметов из различных классов и сообщения ему не только названия предмета, но и, возможно, его описания. Это обучение ведется человеком в диалоговое режиме, позволяющем оперативно выявлять и исправлять ошибки робота. Во-вторых, специфика задачи ярко проявляется в большой вариативности изображений реальных предметов и сцен, которая имеет двоякую природу. С одной стороны, она порождается естественной вариативностью характеристик самих предметов, с другой стороны, - перемещением предметов в пространстве. Вариативность второго рода можно трактовать как результат действия некоторых известных преобразований изображения. Априорное знание этих преобразований позволяет построить алгоритм распознавания t инвариантный по отношению к этим преобразованиям. Благодаря этому удается не только "избавиться" от вариативности второго рода, но и существенно облегчить задачу переработки зрительной информации.

Сама эта задача подразделяется на следующие подзадачи: описание классов (формирование понятий о классах объектов), распознавание изображения данного предмета, анализ изображения сцены (распознавание всех предметов на сцене). Результаты решения перечисленных подзадач могут использоваться для моделирования внешней среды (на четвертом уровне иерархии) путем преобразования изображений предметов и сцен в их пространственное представление, а также для описания сцен на естественном языке или, наоборот, для синтеза изображения сцены по ее описанию.

Рассмотрим сначала задачу описания классов (формирования понятий). Эта задача решается в режиме обучения. Роботу последовательно предъявляют предметы из . различных классов (и, возможно, в различных ракурсах) с указанием, к какому классу каждый такой предмет принадлежит. Эти предметы (а также их изображения) называют эталонными, а совокупность классифицированных предметов - обучающей выборкой. По этим данным робот должен автоматически сформировать описание классов в терминах тех свойств предметов, которые непосредственно измеряются сенсорной системой. Примерами этих свойств, которые мы будем называть первичными признаками, являются следующие: "красное", "ближе", "правее", "выше", "две точки соединены отрезком", "два отрезка параллельны", "зоны одинаковой яркости" и т. п. Таким образом, изображения предметов и сцен задаются полным набором своих первичных признаков.

Каждому признаку поставим в соответствие предикат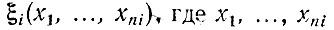  

- элементы изображения ω, определяющие наличие на нем i-го признака. Тогда каждому эталону ω_k (предмету из обучающей выборки) соответствует набор значений предикатов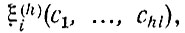  

истинных на изображении данного предмета ω_k. Здесь c_j - предметные константы, означающие фиксированные части изображения. Описанием изображения эталона ω_k будем называть конъюнкцию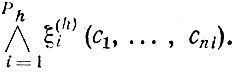  

Поскольку к одному и тому же классу могут принадлежать несколько эталонов (например, предмет из этого класса, показанный в разных ракурсах), то описанием всех эталонных изображений, принадлежащих данному классу Ω_k, является дизъюнкция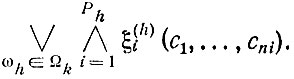  

Если теперь в этой дизъюнкции все предметные константы c заменить на соответствующие предметные переменные x_j, то получим ППФ, которую естественно назвать описанием класса Ω_k. Введем предикат σ(k), означающий принадлежность изображения классу Ω_k. Тогда каждый класс Ω_k описывается аксиомой класса (АК) вида

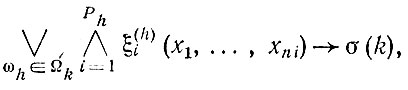
которая по существу является логическим определением класса (или соответствующего ему понятия). Из вышеизложенного ясно, что АК вида (5.1) могут строиться роботом автоматически в режиме обучения по мере последовательного предъявления ему эталонов.

Практически важно, чтобы система АК обладала свойствами полноты, независимости и инвариантности в естественных смыслах. Дадим развернутое определение этих свойств.

Систему АК будем называть полной на множестве изображений {ω}, если для всякого изображения со из этого множества найдется АК, принимающая на нем значение "истинно". Следует отметить, однако, что полнота системы АК не исключает того, что для некоторого изображения могут найтись две АК, принимающие на нем значение "истинно".

В некоторых случаях требуется, чтобы ни одно исследуемое изображение не было отнесено одновременно к нескольким классам (например, если априори известно, что распознаваемые классы изображений не пересекаются). Это требование должно быть отражено в АК. Систему АК будем называть непротиворечивой, если существует только одна АК, истинная на любом данном изображении. Из приведенного определения следует, что непротиворечивая система АК исключает возможность пересечения классов, описываемых этой системой аксиом. Очевидно, что непротиворечивость системы АК всегда можно эффективно проверить.

Вариативность изображений, порождаемая пространственными преобразованиями воспринимаемых предметов, а также действием разного рода помех и искажений, требует, чтобы система обладала определенной инвариантностью и помехозащищенностью. Например, всевозможные изображения стола, отличающиеся от эталонного (по которому строится соответствующая АК) сдвигом, поворотом, масштабом, а также некоторыми незначительными искажениями или помехами (лишние линии, незначительные изменения пропорций и т. п.), должны описываться одной и той же АК "стол", т. е. должны классифицироваться как эквивалентные. Систему АК будем называть инвариантной по отношению к заданной группе преобразований, если каждая входящая в нее аксиома принимает одно и то же значение на изображениях, отличающихся преобразованиями из этой группы. Таким образом, инвариантность системы АК позволяет "снять" охарактеризованную выше вариантность изображений и тем самым облегчить распознавание сцен по их изображениям.

Задачи распознавания и анализа изображений могут быть переформулированы как задачи логического вывода. Эти задачи решаются в режиме распознавания. Роботу предъявляются сцена, изображение ω˜ которой может содержать одно или несколько изображений предметов. Эти изображения отличаются от эталонов некоторыми преобразованиями и даже могут частично перекрываться. Описание изображения сцены S(ω˜) представляет собой конъюнкцию всех первичных предикатов, истинных на данном изображении ω˜. В этих условиях задача отыскания на изображении ω˜ изображения из определенного класса Ω_k, т. е. задача распознавания, сводится к нахождению доказательства теоремы S(ω˜) → σ(k). Саму эту теорему можно трактовать как вопрос: имеется ли на данном изображении ω˜ предмет из k-го класса? Ясно, что в процессе ответа на этот вопрос описание S(ω˜) может быть использовано не полностью. Поэтому измерение тех или иных первичных признаков и предикатов должно производиться по мере необходимости в процессе логического вывода.

Задача анализа изображения сцены заключается в распознавании на ней всех изображений предметов из различных классов. Формально эта задача сводится к последовательному доказательству теорем S_i(ω˜) → ∃kσ(k), i = 1, ..., N - 1, где S₁(ω˜) = S(ω˜), a S_i+1(ω˜)получается из S_i(ω˜) вычеркиванием всех предикатов, участвовавших в выводе i-й теоремы. Содержательно это означает, что, как только выделяется очередное изображение предмета из некоторого класса, оно при дальнейшем анализе не рассматривается. Полный анализ изображения сцены заканчивается распознаванием (и тем самым выделением) всех видимых изображений предметов, составляющих сцену.

В режиме обучения и распознавания на различных изображениях может встречаться один и тот же набор первичных признаков, характеризующих, например, фрагмент изображения. В таких случаях естественно ввести вторичные признаки, каждый из которых представляет собой некоторую совокупность из первичных признаков, а также вторичные предикаты, определяющие соответствующие фрагменты изображения как новые понятия. Аксиомами обучения (АО) будем называть ППФ вида

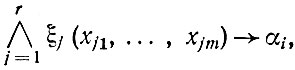
где ξ_j(х_j1, ..., х_jm), j = 1, ..., r - первичные предикаты, дающие полное описание вторичного предиката α₁, т. е. определяющие некоторый фрагмент изображения как новое понятие. Использование АО позволяет не только более экономно представить АК, но и повысить эффективность системы логического вывода в процессе распознавания и анализа.

Как мы уже отмечали, универсальным средством логического вывода в исчислении предикатов является метод резолюций. Поэтому любой конкретный алгоритм распознавания или анализа определяется стратегией метода резолюций. Важно отметить, что для распознавания на изображении сцены нужного предмета не обязательно строить доказательство теоремы S(ω˜) → σ(k) полностью, т. е. перебирать все элементы искомого простого изображения на изображении сцены ω˜. Вместо этого достаточно найти фрагмент искомого изображения, который содержится лишь в изображениях k-го класса и не содержится ни в одном изображении предметов из других классов. Именно это обстоятельство позволяет сильно ограничить число, шагов логического вывода, а также распознавать частично закрытые изображения предметов.

Качество работы алгоритмов распознавания и анализа естественно характеризовать числом обращений к информационно-измерительной (сенсорной) системе с целью определения нужных признаков. Заметим, что в нашей формализации это в точности совпадает с числом шагов логического вывода, т. е. с числом резольвент, формируемых в процессе распознавания и анализа. Стратегию логического вывода будем называть оптимальной, если число шагов доказательства (число резольвент) минимально.

Важно, отметить, что система логического вывода способна совершенствовать алгоритму распознавания и анализа за счет использования элементов обучения, а именно: АО и адаптивной подстройки стратегии. Адаптивная подстройка стратегии осуществляется путем ее перестройки (например, путем перестройки оптимального распознающего графа) по мере распознавания новых изображений и формирования аксиом обучения (АО). Использование АО сокращает логический вывод на длину ее описания, а процесс построения оптимального распознающего графа - на значение экспоненциальной функции от этой длины [11].

Проиллюстрируем описанный метод на примере решения задачи описания, распознавания и анализа обстановки в цехе. Предположим, что в результате предварительной фильтрации исходные изображения предметов и сцен превращаются в контурные изображения, составленные из отрезков. Введем необходимые для дальнейшего первичные признаки и предикаты, представленные в табл. 5. Вторичные признаки и предикаты (аксиомы обучения) представлены в табл. 6. В режиме обучения роботу предъявляются эталонные контурные изображения токарного и сверлильного станков, представленные на рис. 12. По этим данным он строит АК, общий вид которых приведен в табл. 7. Так в режиме обучения автоматически формируется описание классов.

Таблица 5

Таблица 6

Таблица 7

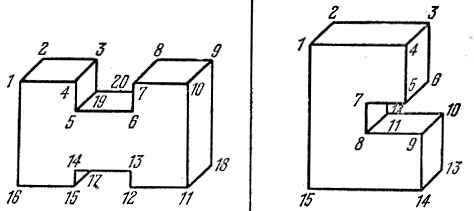
Рис. 12. Эталонные изображения (режим обучения)

В режиме распознавания роботу предъявляется изображение произвольной сцены - обстановки в цехе, попавшей в "поле зрения" робота. Для определенности пусть это будет изображение сцены, представленное на рис. 13. Описание этой сцены (на языке первичных и вторичных предикатов) имеет вид

1. ВПР (6, 5, 2, 1); 2. ГПР (5, 2, 3, 4); 3. ВТ (17, 4); 4. ГР (17, 16); 5. ВПР (16, 15, 14, 18); 6. ГР (19, 18); 7. ГПР (15, 14, 13, 12); 8. ВТ (И, 12); 9. ГР (10, 11); 10. ВТ (10, 9); 11. ГР (10, 20); 12. ГР (8, 9,); 13. ВТ (7, 8); 14. ГР (6, 7); 15. ВТ (30, 28); 16. ГР (29, 28); 17. ГР (29, 27); 18. ВТ (21, 27); 19. ГР (22, 21); 20. ВТ (23, 22); 21. ГР (23, 24); 22. ВТ (25, 24); 23. ГР (26, 25); 24. ВТ (26, 29); 25. ГР (26, 31).

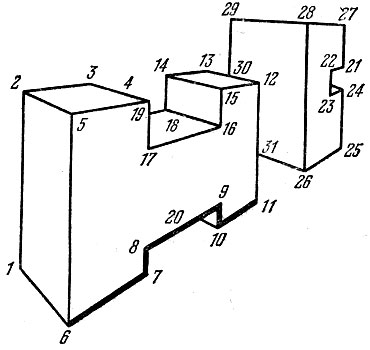
Рис. 13. Изображение сцены (режим распознавания)

Предположим, что мы спрашиваем робота (или он сам задается этим вопросом): "есть ли на изображении сцены токарный станок?". Для ответа на вопрос робот пытается доказать теорему

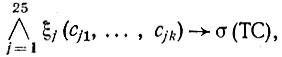
где ξ_j(c_j1, ... , c_jk), j = 1, ... , 25, - предикаты, входящие в приведенное выше описание изображения сцены. Доказательство этой теоремы с помощью стратегии лозы [9] потребовало в зависимости от порядка записи АК от 8 до 54 резольвент. Однако, как уже отмечалось, для распознавания токарного станка на изображении сцены полное доказательство соответствующей теоремы не обязательно, - возможно распознавание по фрагменту. Использование оптимальной стратегии в этом примере позволило сократить число резольвент до 5. При этом был автоматически выделен и существенно использовался в процессе логического вывода фрагмент изображения, обведенный на рис. 13 жирной линией. Интересно отметить, что решение той же задачи без использования АО приводит к существенному снижению эффективности системы логического вывода. В этом случае описание изображения сцены требует уже не 25, а 47 первичных предикатов. В процессе распознавания токарного станка с помощью стратегии лозы строится по меньшей мере 73 резольвенты.

Резюмируя содержание разделов 3-5, отметим, что язык исчисления предикатов и адаптивная система логического вывода позволяют эффективно решать не только задачу автоматического планирования поведения робота в условиях априорной неопределенности, но и задачи описания классов, распознавания и анализа ситуаций в окружающей робота среде.