7. Алгоритмы построения программных движений

Задача построения программных движений (ПД) робота решается на пятом уровне иерархии его системы управления. Особенность этой задачи заключается в том, что движение исполнительных механизмов робота задается законом изменения обобщенных координат, а происходит в реальной внешней среде. При этом допустимость тех или иных конфигураций исполнительных механизмов непосредственно наблюдается в реальной же среде и никаким простым способом не выражается "на языке" пространства обобщенных координат. Другой особенностью является наличие двигательной избыточности, присущей роботам с большим числом степеней свободы. Эта избыточность, однако, полезна. Она позволяет среди множества возможных ПД отобрать наиболее "экономные", оптимальные программные движения.

Рассмотрим кратко некоторые идеи и алгоритмы построения ПД. Эти алгоритмы служат для того, чтобы робот мог, еще не совершая каких-либо реальных движений, "мысленно" рассчитать, а если нужно - скорректировать программу своих целенаправленных движений.

В качестве примера рассмотрим задачу управления многозвенным манипулятором. Цель управления в этом случае заключается в отслеживании схватом некоторой "траектории, рассчитанной на более высоком уровне планирования поведения. Задача осложняется наличием разного рода препятствий и конструктивных ограничений. Программным движением называется такой закон изменения обобщенных координат, при котором достигается цель управления, удовлетворяются конструктивные ограничения и обеспечивается обход препятствий.

Идея "глобального" подхода к построению ПД заключается в следующем. Вначале на основе информации о траектории схвата с учетом конструктивных ограничений и препятствий формируется план движения - последовательность промежуточных конфигураций, ведущая к цели. Затем по "кускам" (например, в классе кусочно-полиномиальных функций) строится само ПД в соответствии с этим планом.

Большой интерес представляет также "локальный" подход, основанный на моделировании так называемого тропизма. Тропизм - это свойство, присущее простейшим живым организмам; оно заключается в направленных движениях организмов в результате действия односторонних раздражителей. Применительно к уровню построения ПД под таким "раздражителем" будем понимать информацию о взаимном расположении манипулятора и препятствий в реальном трехмерном пространстве, а под тропизмом - движения манипулятора, направленные на удаление от препятствий. Не приводя (ввиду громоздкости) явные формулы алгоритма построения ПД, имитирующего свойства тропизма, отметим только, что синтезируемые им целенаправленные движения реализуются за счет двигательной избыточности манипулятора, в то время как схват движется по заданной траектории.

Мы бегло охарактеризовали различные способы построения ПД манипулятора. А как строить ПД колесного или гусеничного шасси для робота, функционирующего на местности с препятствиями? Эта задача естественным образом распадается на две: прокладка безопасного маршрута и построение закона изменения обобщенных координат, удовлетворяющего конструктивным ограничениям и обеспечивающего движение по этому маршруту.

Рассмотрим один из подходов к построению оптимального маршрута на местности с препятствиями, основанный на методе динамического программирования. Для простоты предположим, что местность представляет собой плоскость, а препятствия задаются ломаными линиями. Пусть заданы координаты исходной точки (где находится робот) и целевой точки (куда он должен передвинуться). Задача заключается в построении маршрута (ломаной линии) из исходной точки в целевую, который не пересекает ломаных препятствий и имеет наименьшую длину. Такой маршрут будем называть оптимальным.

Прежде всего заметим, что если сформулированная задача не имеет тривиального решения (когда маршрутом является просто отрезок, соединяющий исходную и целевую точки), вершинами ломаной наименьшей длины должны быть вершины ломаных - препятствий. Поэтому в дальнейшем будем рассматривать только эти вершины. Введем функцию f_i, определяющую минимальную длину пути из некоторой точки i в целевую точку. Сразу же возникает вопрос - как найти эту функцию? Один из классических способов нахождения функции состоит в том, чтобы задать уравнения, определяющие эту функцию.

Приступая к поиску такого уравнения, зададимся вопросом: существует ли такое внутреннее свойство процесса поиска оптимального пути, которое можно использовать для получения уравнения? Ответ, к счастью, положительный. В самом деле, анализируя задачу, мы видим, что отправляясь из точки i, робот на первом шаге попадет в точку j, пока неясно, какую именно. Далее, мы замечаем, что, если робот ищет кратчайший путь от точки i до целевой точки, то в какую бы точку он ни попал, путь из точки j в целевую должен иметь наименьшую длину. Это почти очевидное свойство докажем от противного. Пусть путь из точки i в целевую точку является кратчайшим, тогда часть пути из точки j в целевую точку также должна иметь минимальную длину, так как, если бы эта часть пути не была кратчайшей, то ее можно было бы заменить более кратким путем и тем самым сократить общую длину пути, а это противоречит тому, что f_i по определению есть минимальная длина пути.

Таким образом, мы установили существенное внутреннее свойство процесса поиска оптимального маршрута: "хвост" (конец) процесса - это всегда кратчайший маршрут. Что все это дает для определения функции f_i? Обозначим через s_ij - длину пути между точками i и j (хотя все еще неизвестно, что это за точка j), а через f_j - наименьшую длину пути между точкой j и целевой точкой. Выбирая в качестве точки j такую точку, которая минимизирует сумму s_ij + f_j, получаем уравнение

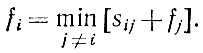
Это - основное уравнение динамического программирования. Оно обладает тем свойством, что задает две функции f_i и j(i). В самом деле, если мы нашли f_i, то значение j, на котором достигается минимум (5.3), как раз и указывает ту точку, в которую роботу нужно двигаться дальше. Важно отметить, что функция j(i) представляет собой по существу стратегию поиска оптимального маршрута, т. е. правило, которое позволяет роботу, находящемуся в произвольной точке i, определить, куда ему следует двигаться дальше.

Трудность решения уравнения (5.3) заключается в том, что неизвестная функция входит в обе части равенства. В такой ситуации приходится прибегать к классическому методу последовательных приближений в функциональном пространстве, используя рекуррентную формулу

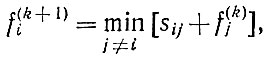
где f_i^(k) - k-e приближение искомой функции. Можно доказать сходимость алгоритма (5.4) для произвольной неотрицательной начальной функции f_i⁰ с единственным ограничением, что значение функции f в целевой точке равно нулю.

Решение уравнения (5.3) можно искать и в пространстве стратегий. Этот путь представляется более естественным: "мыслить" в терминах пространства стратегий роботу более удобно, чем в терминах искусственно выбранных функций f_i. К тому же понятие стратегии сохраняет смысл и в тех случаях, когда функция не может быть определена. Какую же приближенную стратегию можно выбрать в задаче прокладки оптимального маршрута? Одна из возможных стратегий такова: робот решает непосредственно двигаться из точки i в целевую точку. Тогда получается приближение f_i⁽⁰⁾ = s_iц, где s_iц - длина пути между точкой i и целевой точкой. Следующее приближение получится, если робот будет искать решение в классе двухзвенных ломаных. Дальнейшие приближения ищутся в классе трехзвенных, четырехзвенных и т. д. ломаных.

Одно из преимуществ выбора приближений в пространстве стратегий состоит в следующем: выбрав из общих соображений стратегию,.мы тут же получаем соответствующую функцию f_i^(k). Понятно, что f_i^(k) ≤ f_i. В заключение, не входя в детали, отметим только, что описанный метод последовательных приближений в пространстве стратегий действительно сходится к решению уравнения (5.3) и допускает чрезвычайно простую программную реализацию.

После того, как оптимальный безопасный маршрут построен, можно тем или иным методом (например, с помощью кусочно-полиноминальной аппроксимации) построить программное движение колесного или гусеничного шасси робота. Алгоритмическое решение этой последней задачи обычно не вызывает никаких принципиальных затруднений.