2. Постепенные отказы

Воспользуемся условием устойчивости системы привода, полученным в § 3 гл. 2, и определим вероятность того, что неравенство (99) соблюдается в заданный момент времени, несмотря на постепенные отказы элементов системы. Эта вероятность есть

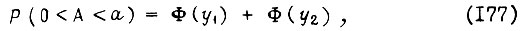
где через 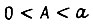записано неравенство (99):

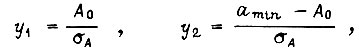
где 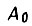- среднее значение A; 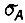- среднеквадратическое отклонение 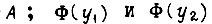определяем по таблицам функции Лапласа. В качестве 40 выбираем исходное значение A, полученное в результате синтеза динамики системы. Величину 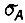находим из формулы

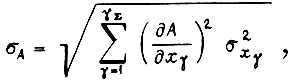
где 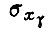- среднеквадратическое отклонение параметра 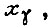от которого зависит A.

Из формул 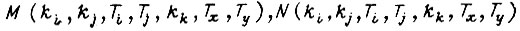с учетом 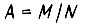получаем

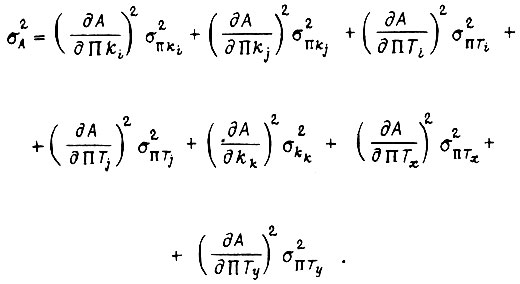
Пусть соблюдается условие 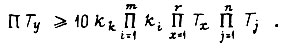Тогда при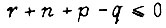

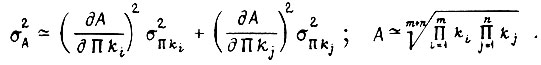
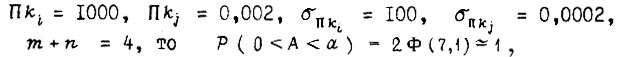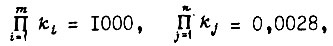
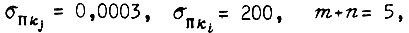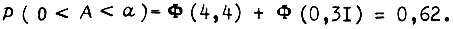Если т. е. система привода является очень надежной. Если то При 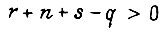и отношении 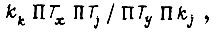равном 3,8 со среднеквадратическим отклонением 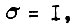получаем 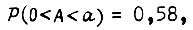если 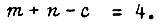При вычислении вероятности среднеквадратические отклонения отдельных параметров системы на практике могут быть заданы по известному правилу "3σ".

Вероятность смещения кривой переходного процесса системы 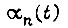при постепенных отказах определим, полагая, что передаточная функция апериодического звена

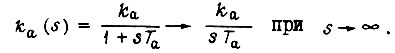
Подставив аппроксимированные функции звеньев в уравнение (95), получаем

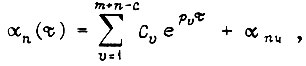
где 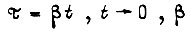- число раз, в которое изменился вовремя эксплуатации привода модуль комплексного числа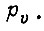

При 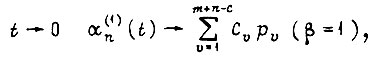т. е. 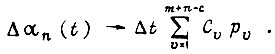Аналогично

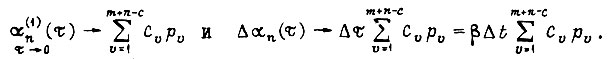
На отрезке 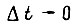отношение

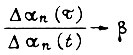
или

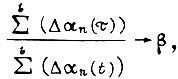
где b - любое целое число отрезков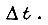

Вероятность изменения кривой 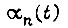не более чем в β раз по оси 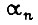или по оси t

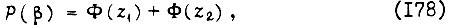
где 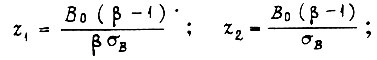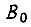- среднее значение модуля B комплексного числа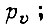 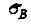- среднее значение модуля B комплексного числа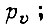 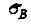- среднеквадратическое отклонение модуля .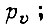

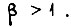Величина модуля :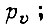

при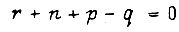

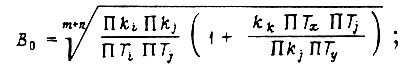
при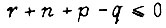

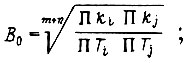
при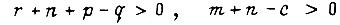

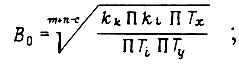
при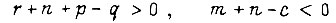

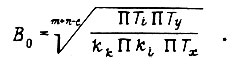
Пусть в одном из случаев 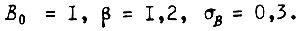Тогда из

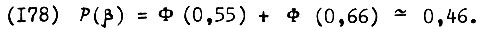
В системе электропривода, построенной по принципу подчиненного регулирования (для одной степени свободы робота), объект регулирования внутри каждого контура представим состоящим из двух апериодических звеньев: с большой постоянной времени 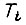и малой 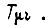Настройка контуров производится по "модульному критерию". Передаточная функция системы с пятью контурами имеет вид

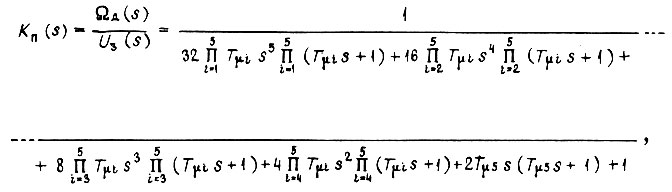
где i - номер контура; 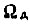- скорость вращения вала привода. При 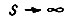передаточная функция

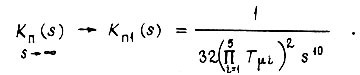
По виду 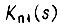для пяти контуров запишем 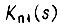системы с числом контуров, равным ρ:

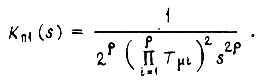
Оригинал 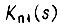есть

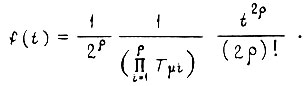
При настройке контура по "модульному критерию"

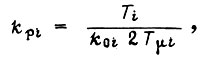
где 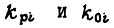- коэффициенты передачи регулятора и объекта.

Учитывая, что на произвольном отрезке 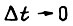приращение 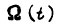равно приращению 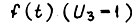только при нулевых начальных условиях на этом отрезке, и исходя из неразрывности производных 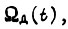запишем

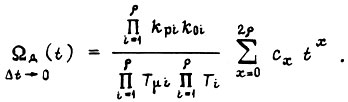
При

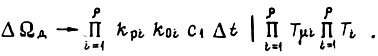
Предположим, что из-за постепенных отказов элементов системы коэффициент при Δt в формуле 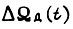изменяется в β раз. Тогда отношение 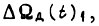соответствующее новым значениям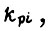 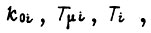к исходному 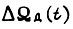на отрезке 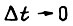есть

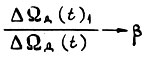
или

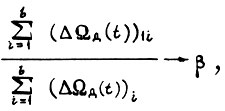
где b - любое целое число отрезков Δt.

Вероятность изменения кривой 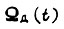не более чем в β раз по оси 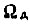и по оси t

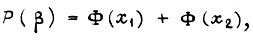
где 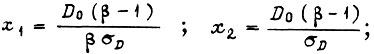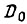- среднее значение величины

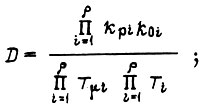
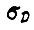
- среднеквадратическое отклонение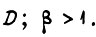

Вычисление 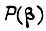производится аналогично вычислению 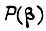(178). Вероятность 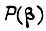тем больше, чем меньше 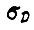, т. е. чем меньше среднеквадратические отклонения 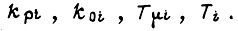При 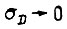вероятность 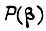стремится к единице.

Рассмотрим постепенные отказы силовой части привода с асинхронным электродвигателем, на статорную обмотку которого поступает от инвертора напряжение ступенчатой формы.

Одной из задач проектирования является обеспечивание надежного диапазона регулирования скорости вращения привода. При заданных моменте статической нагрузки и верхней граничной скорости диапазон определяется в большой степени неравномерностью вращения вала, вызванной ступенчатостью форм фазных напряжений на обмотке статора. Из дифференциального уравнения (74), описывающего электромеханический переходный процесс двигателя на отрезке 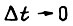, где практически можно принять постоянными 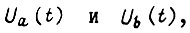имеем

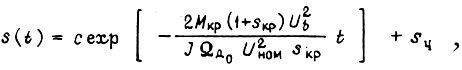
где 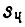- частное решение; J - момент инерции привода; 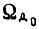- скорость идеального холостого хода на нижней границе диапазона регулирования Ω; c - постоянная.

Очевидно, при 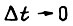можно записать

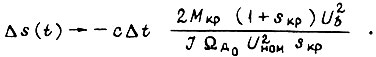
Предположим, что из-за постепенных изменений параметров системы величина 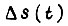изменилась в ее раз, т. е. 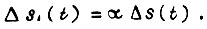При постоянстве 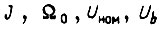это связано со смещением отношения

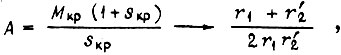
если частота инвертора стремится к нулю. Здесь 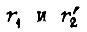- активные сопротивления фазы двигателя в статорной и роторной цепях. Вероятность изменения 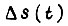не более чем в α раз находим по формуле

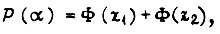
где

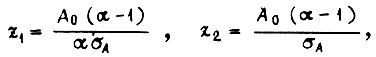
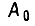
- среднее значение A; 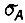- среднеквадратическое отклонение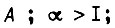

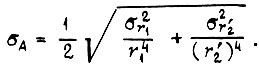
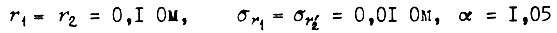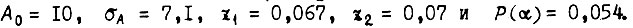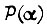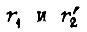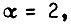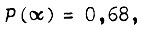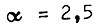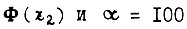При получаем Столь малая величина дает основание утверждать, что в данном примере система электропривода практически не имеет надежности в условиях изменения во времени . Если же то и в этом случае система более надежна. Взяв для для 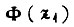характеризующей снижение колебаний s, получаем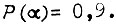

Итак, система привода является весьма надежной, если при ее эксплуатации увеличение 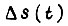в 2,5-3 раза по сравнению с исходным значением является удовлетворительным. Это изменение 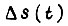соответствует такому же увеличению амплитуды-колебаний s, если синусоидальное колебание заменить треугольным, т. е. принять постоянную с, определяемую из начальных условий, одинаковой для всех отрезков времени .

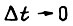Обеспечить желаемый диапазон регулирования скорости с учетом колебаний скольжения можно, увеличивая момент инерции привода J до величины, зависящей от α и полного перепада скольжения внутри колебания. Кроме того, для той же цели можно образовать обратные связи в системе по напряжению, току либо магнитному потоку асинхронного двигателя. Рассмотрим случай, когда реализована обратная связь по току статора двигателя, действие которой сводится к увеличению напряжения выпрямителя 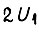с увеличением момента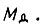

Действие обратной связи по току гармоники частоты к позволяет при 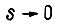получить вместо напряжения 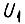напряжение

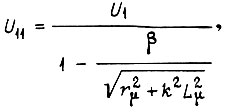
где 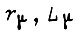- параметры контура намагничивания двигателя; β - коэффициент пропорциональности.

Вероятность 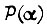смещения кривой 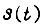теперь вычисляется при 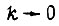из условия изменения в α раз величины

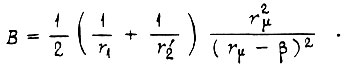
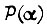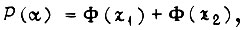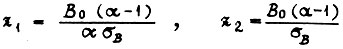Вероятность равна сумме где - среднее значение B,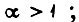 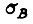- среднеквадратическое отклонение B.

Величину 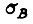определим по формуле

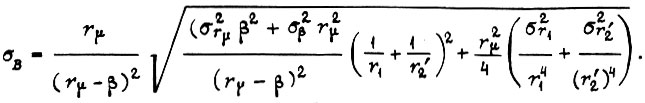
Вычисляя 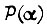, находим α, для которого 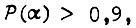что дает возможность оценить смещение амплитуды колебаний скольжения s для выбранных момента инерции привода J и коэффициента β. Амплитуда колебаний должна быть меньше или равной заданной.

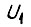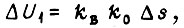В системе привода с автономным инвертором, замкнутой по скорости вращения вала, приращение напряжения есть где 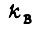- коэффициент передачи канала управления выпрямителем; 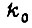- коэффициент обратной связи.

Приращение скольжения в переходном процессе на отрезке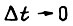

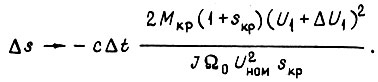
Для малых значений 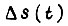приближенно

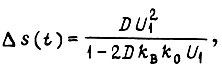
где 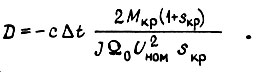Среднеквадратическое отклонение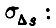

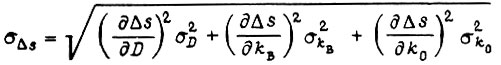
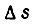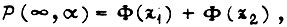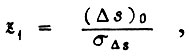
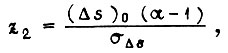
Вероятность смещения из-за постепенных изменений параметров схемы где 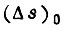- исходное значение .

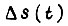В результате вычислений 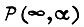фиксируется α, для которого 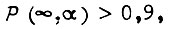и гарантируется с этой вероятностью диапазон регулирования скорости вращения привода для выбранных J,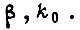

После того как обеспечена надежность системы по постепенным отказам, необходимо рассчитать коэффициент нагрузки элементов 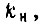исходя из целесообразной надежности по внезапным отказам.