
Глава 5. Вопросы надежности систем привода
1. Энергетическая оценка сравнительной надежности систем привода
Оценка надежности предполагает наличие статистических сведений. К оценке по внезапным отказам относятся λ-характеристики. Однако для ряда новых элементов и самых разнообразных режимов эксплуатации привода эти характеристики могут отсутствовать или быть малодостоверными. В этом случае целесообразно определение сравнительной надежности устройств. Нике рассматривается энергетический метод сравнения отдельных вариантов. Сравнение связано с выявлением различия в количестве элементов, в величине и типе нагрузок и в их продолжительности.
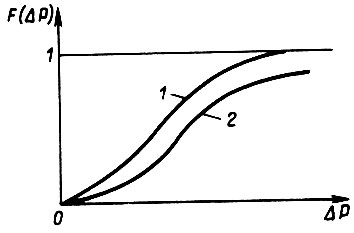
Рис. 80
Представим внезапный отказ элемента как результат его внутреннего износа от случайных воздействий. Мощность случайного источника, трансформированная в схему, может иметь проявление как электрическая, механическая и т. п. мощность. График функции распределения случайной величины трансформированной мощности показан на рис. 80 (кривая 1). Сделаем следующие допущения:
- случайные воздействия на отдельные элементы являются независимыми событиями;
- схема нерезервирована;
- схема невосстанавливаема.
Если 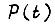 - мощность, выделяющаяся в данном элементе в функции времени, а
- мощность, выделяющаяся в данном элементе в функции времени, а 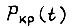 - некоторая критическая рассеиваемая мощность, приводящая к износу элемента за время
- некоторая критическая рассеиваемая мощность, приводящая к износу элемента за время 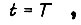 то разность между ними
то разность между ними 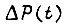 есть мощность случайного источника, т. е.
есть мощность случайного источника, т. е.
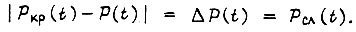
Вероятность выхода системы привода из строя определим по формуле полной вероятности
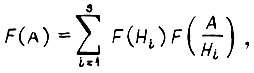
где А - рассматриваемое событие;  -я гипотеза о появлении случайной мощности, причем
-я гипотеза о появлении случайной мощности, причем 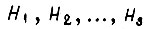 представляют полную группу несовместных событий. Набор гипотез соответствует полному набору возможных кривых
представляют полную группу несовместных событий. Набор гипотез соответствует полному набору возможных кривых 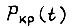 элементов. Формулу для
элементов. Формулу для 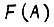 перепишем в ином виде, учитывая только гипотезы, для которых
перепишем в ином виде, учитывая только гипотезы, для которых 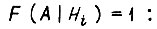
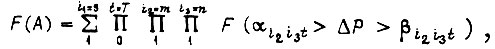
где s - число гипотез; Т - срок службы схемы; m - число элементов схемы; n - число типов изнашивающей нагрузки; 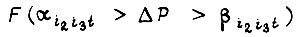 - вероятность воздействия
- вероятность воздействия 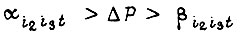 Для фиксированного элемента
Для фиксированного элемента 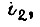 фиксированного типа нагрузки
фиксированного типа нагрузки 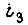 в момент времени t. Получаем предельное выражение для
в момент времени t. Получаем предельное выражение для 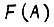 , предположив, что каждый последующий момент времени лежит бесконечно близко к предыдущему
, предположив, что каждый последующий момент времени лежит бесконечно близко к предыдущему
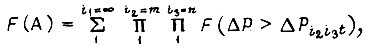
где под 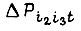 следует понимать случайное значение мощности определенного типа нагрузки, мгновенно изнашивающей данный элемент в некоторый фиксированный момент времени t или значение мощности в данном элементе, соответствующее мгновенному износу другого элемента.
следует понимать случайное значение мощности определенного типа нагрузки, мгновенно изнашивающей данный элемент в некоторый фиксированный момент времени t или значение мощности в данном элементе, соответствующее мгновенному износу другого элемента.
Вероятность отказа схемы 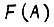 тем больше, чем больше разность
тем больше, чем больше разность 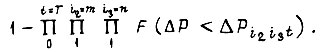
Частные законы для плотности распределения случайной величины x могут быть получены из общего выражения
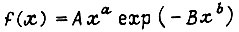
путем подстановки коэффициентов 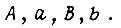 Если
Если 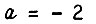 и
и 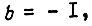 то
то
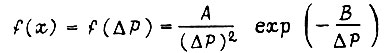
и при 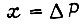
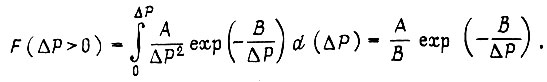
Выражение для вероятности отказа схемы получит вид
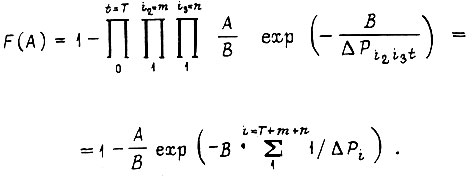
Отказ схемы тем вероятней, чем больше сумма 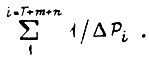
Покажем, что этот вывод справедлив для любых значений коэффициентов 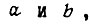 для которых функция
для которых функция 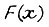 имеет вид кривой 1 (см. рис. 80). Кривая 2 изображает функцию
имеет вид кривой 1 (см. рис. 80). Кривая 2 изображает функцию 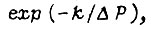 все точки которой лежат правее
все точки которой лежат правее 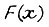 . Предположим,что для функции
. Предположим,что для функции 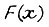 надежность двух сравниваемых вариантов определяется неравенством
надежность двух сравниваемых вариантов определяется неравенством
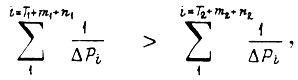
т. е. 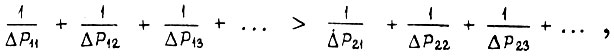
где 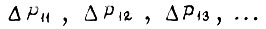 - значения случайной мощности доя первого варианта и
- значения случайной мощности доя первого варианта и 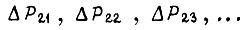 - аналогичные значения для второго варианта. Из этого неравенства заключают о меньшей надежности первого варианта. Для того, чтобы первый вариант остался менее надежным при сравнении схем по кривой 2, необходимо соблюдение неравенства
- аналогичные значения для второго варианта. Из этого неравенства заключают о меньшей надежности первого варианта. Для того, чтобы первый вариант остался менее надежным при сравнении схем по кривой 2, необходимо соблюдение неравенства
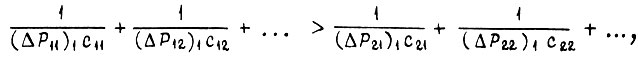
где 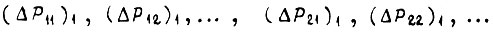 - значения отдельных мощностей, отсчитываемых по кривой 2, для которых вероятности отказов элементов остаются теми же, что и для
- значения отдельных мощностей, отсчитываемых по кривой 2, для которых вероятности отказов элементов остаются теми же, что и для 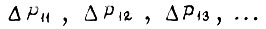 ,
, 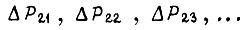 отсчитываемых по кривой 1. Каждый из коэффициентов
отсчитываемых по кривой 1. Каждый из коэффициентов 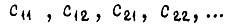 меньше единицы, что следует из рис. 80. Этому неравенству равносильно неравенство
меньше единицы, что следует из рис. 80. Этому неравенству равносильно неравенство
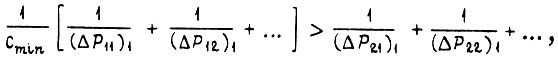
где 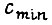 - минимальный коэффициент из всех
- минимальный коэффициент из всех 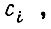 расположенных в левой части неравенства.
расположенных в левой части неравенства.
Но для кривой 2 согласно доказанному выше отказ первого варианта вероятней отказа второго, если соблюдается неравенство
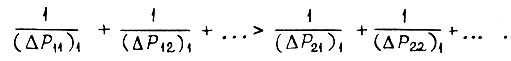
Следовательно, тем более справедливо неравенство
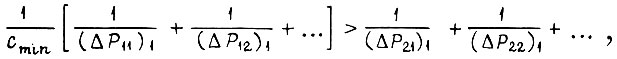
а также предположение о том, что для любых коэффициентов 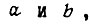 для которых функция
для которых функция 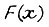 имеет вид кривой 1, отказ схемы тем вероятней, чем больше сумма
имеет вид кривой 1, отказ схемы тем вероятней, чем больше сумма 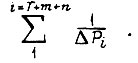 Так как мощность есть энергия, рассеиваемая в единицу времени, то физический смысл этой суммы состоит из определении времени, которое необходимо расходовать на единицу энергии,разрушающей схему. Схема, для которой это время меньше, более надежна. При этом максимальное время износа любого элемента лежит в пределах бесконечно малого промежутка, что соответствует практически мгновенному износу. Из вида критериальной суммы следует, что анализ сравнительной надежности вариантов эквивалентен рассмотрению системы сумм
Так как мощность есть энергия, рассеиваемая в единицу времени, то физический смысл этой суммы состоит из определении времени, которое необходимо расходовать на единицу энергии,разрушающей схему. Схема, для которой это время меньше, более надежна. При этом максимальное время износа любого элемента лежит в пределах бесконечно малого промежутка, что соответствует практически мгновенному износу. Из вида критериальной суммы следует, что анализ сравнительной надежности вариантов эквивалентен рассмотрению системы сумм
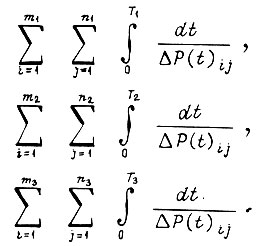
Наименьшая сумма соответствует более надежной схеме. Поскольку в данном случае оценивается надежность по внезапным отказам и 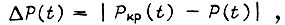 то постепенные возможные изменения во времени мощностей
то постепенные возможные изменения во времени мощностей 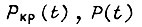 не учитываем. Необходимо иметь в виду, что результаты сравнительной оценки могут оказаться различными, если в понятие элемента вкладывать произвольную величину физического объема изнашиваемого материала, например меди, стали и т. д. Эти результаты являются однозначными, когда под критериальной суммой понимается
не учитываем. Необходимо иметь в виду, что результаты сравнительной оценки могут оказаться различными, если в понятие элемента вкладывать произвольную величину физического объема изнашиваемого материала, например меди, стали и т. д. Эти результаты являются однозначными, когда под критериальной суммой понимается
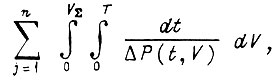
где 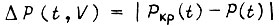 - мощность, приходящаяся на единицу объема устройства в момент времени t и объеме V; n - число типов нагрузки;
- мощность, приходящаяся на единицу объема устройства в момент времени t и объеме V; n - число типов нагрузки; 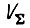 - суммарный объем; T - время эксплуатации.
- суммарный объем; T - время эксплуатации.
Если 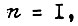 то наиболее надежной схеме соответствует наименьшая сумма
то наиболее надежной схеме соответствует наименьшая сумма 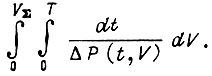
Бели при сравнении двух схем известны сведения о сроке службы одной из них, то для другой схемы получаем информацию о том, больше или меньше срок службы по сравнению с первой. Так можно получить сведения о λ-характеристиках всех преобразователей обучаемой системы привода, сравнивая их всегда с одной схемой. Затем в случае необходимости принимаются меры по резервированию преобразователей или по недогрузке элементов для достижения желаемой надежности привода. Окончательная оценка резервированной системы производится в соответствии с существующей теорией.
Из формулы сравнительной оценки схем следует, что из двух схем с одинаковым числом элементов наиболее надежна та, в которой все элементы имеют большие номинальные мощности и номинально загружены. Этот же вывод содержится в работе [27],в которой экспериментально исследована надежность большого числа электроагрегатов. Автор, в частности, указывает, что в результате количественного определения надежности электроагрегатов было установлено: с возрастанием мощности их надежность имеет тенденцию к повышению.
Применяемый на практике метод λ-характеристик не противоречит полученной критериальной формуле сравнительной оценки. Интенсивность отказов схем вычисляют как сумму 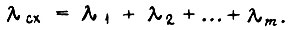 Анализ справочных данных по надежности элементов позволяет представить
Анализ справочных данных по надежности элементов позволяет представить 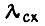 в виде
в виде
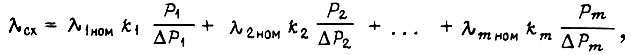
где 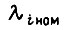 - интенсивность отказа i-го элемента схемы, нагруженного номинально; коэффициенты
- интенсивность отказа i-го элемента схемы, нагруженного номинально; коэффициенты 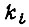 с достаточной точностью для практики являются постоянными;
с достаточной точностью для практики являются постоянными; 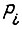 - мощность, рассеиваемая в элементе;
- мощность, рассеиваемая в элементе; 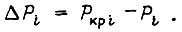
Обычно сведения о том, как зависят коэффициенты 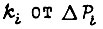 отсутствуют. Сохраняя отношение
отсутствуют. Сохраняя отношение 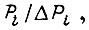 можно подобрать такие
можно подобрать такие 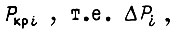 что
что
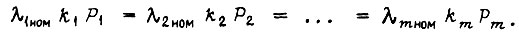
Тогда получаем, что схема, у которое меньше сумма
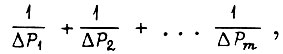
является более надежной.
|
ПОИСК:
|
© ROBOTICSLIB.RU, 2001-2019
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'