Приложение

1. Логические системы привода

Логические схемы, преобразуя двоичные входные сигналы, вырабатывают двоичные выходные сигналы, воздействующие на исполнительные механизмы. Входная информация поступает в логическую схему в общем случае от задающего устройства или оператора,от датчиков пути,скорости момента силы,температуры и т. д., от устройств защиты привода и механизма, от сенсорных датчиков робота и от элементов, фиксирующих отдельные моменты времени. Среди всего разнообразия логических схем выделим четыре типа:

1. с входной информацией, поступающей только от задающего устройства;
2. с входной информацией о времени t и от задающего устройства;
3. с информацией, поступающей от задающего устройства и от датчиков;
4. с информацией, поступающей от задающего устройства и с информацией от датчиков и о времени.

Схема каждого типа может быть комбинированной или последовательностной. Логические системы привода различаются типами входящих в них схем и, кроме того, устройствами, переключающими двигатели, типами двигателей, передаточными свойствами звеньев двигатель-механизм.

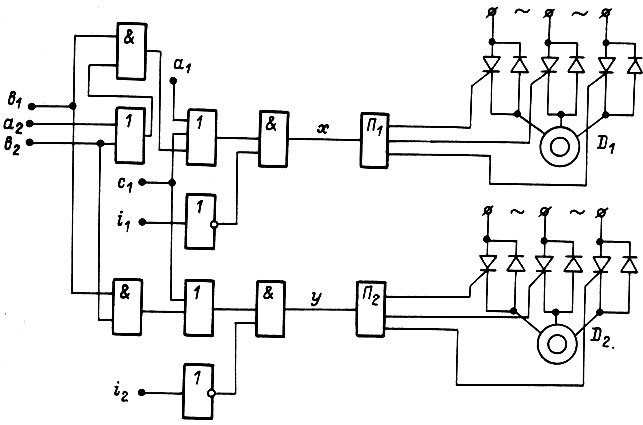
Рис. 82

На рис. 82 изображена комбинационная схема управления асинхронными электродвигателями от входных сигналов 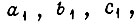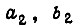(схема третьего типа). Значения сигналов на выходах логической схемы 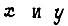определяем по формулам

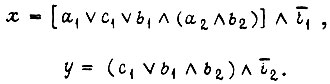
Здесь и далее знаком ∨ обозначена операция логического сложения, знаком ∧ - операция логического умножения для того, чтобы отличать в тексте эти операции от сложения и умножения в десятичной алгебре; 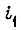- сигнал перегрузки по току двигателя 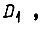используемый для защиты привода; 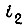- сигнал перегрузки по току двигателя 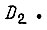Преобразователи 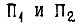преобразуют единичные сигналы на входах в импульсы постоянной частоты, отпирающие тиристоры в цепях обмоток двигателей. Три выхода у каждого преобразователя в данной схеме должны быть не связаны гальванически.

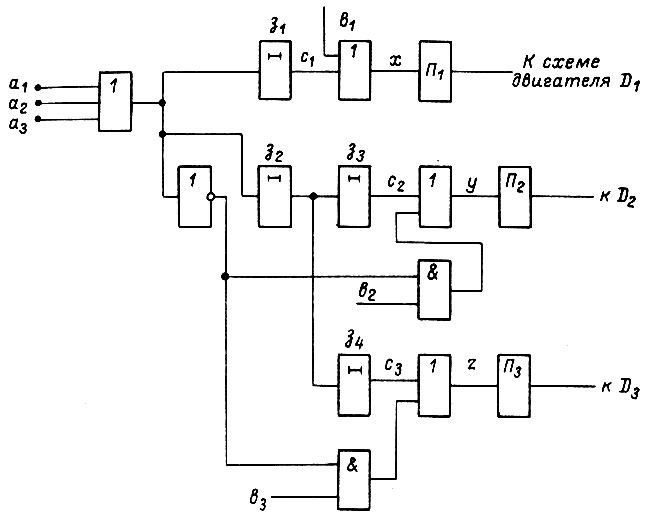
Рис. 83

Схема на рис. 83 иллюстрирует второй тип логических схем. Здесь применены элементы временной задержки в передаче со входа на выход единичного сигнала (после пропадания нулевого) 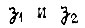и элементы задержки в передаче нулевого сигнала 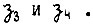Сигналы на входах преобразователей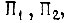

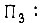
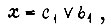
где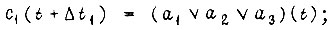

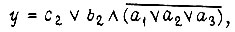
где

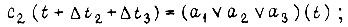
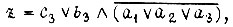
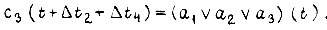
Здесь через 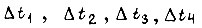обозначены временные задержки в передаче сигналов без преобразования в элементах соответственно 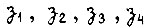Данную схему следует отнести к классу последовательностных.

Представим, что в системе привода робота с цикловым управлением контролируемыми значениями пути для двигателей 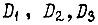являются значения

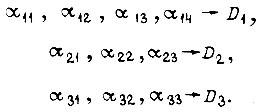
Им соответствуют следующие состояния системы привода 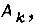в которых она должна находиться по условиям работы:

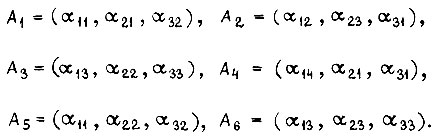
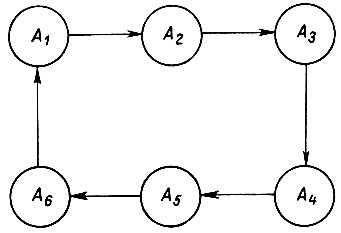
Рис. 84

Направленный граф технологических состояний системы привода показан на рис. 84. Его замкнутость указывает на периодичность движения системы. Последовательность переключений в схеме описывается следующими формулами для 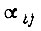в 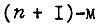технологическом состоянии 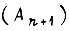в функции 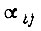в n-м состоянии 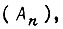т. е. в предыдущем:

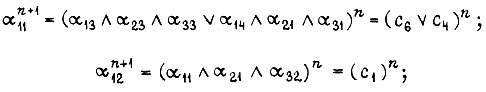
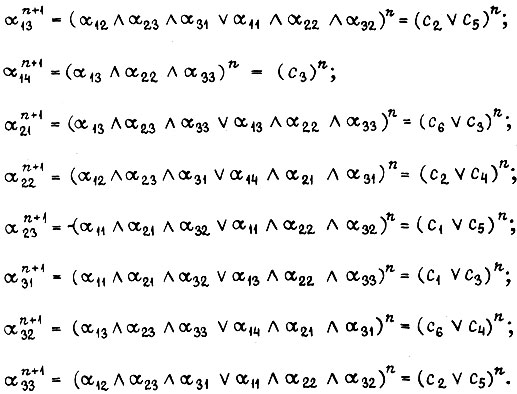
Пусть для комбинации 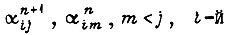i-й двигатель включается в n-м технологическом состоянии системы сигналом 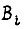для движения вперед, а для 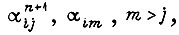- сигналом 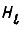для движения назад. Тогда для вышеприведенных 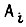и графа (см. рис. 84) получаем

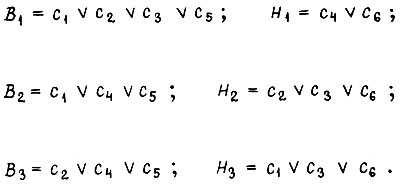
В рассмотренном примере можно построить логическую схему управления двигателями, основываясь на полученных формулах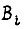

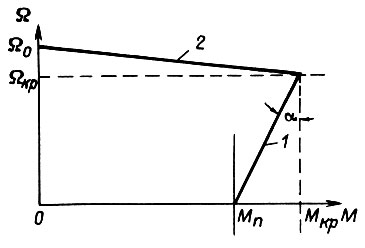
Рис. 85

Предположим,что на вход логической системы привода последовательно во времени поступает информация от датчиков и задающего устройства, а скорость вращения 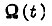каждого двигателя, принадлежащего роботу с цикловым управлением, состоит из трех участков: пуска, движения на среднем участке и торможения. Функция 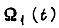описывает пуск двигателя и при 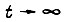- установившиеся движение, а 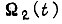- торможение. Для асинхронного электродвигателя с представленной в виде двух прямых на рис. 85, имеем дифференциальное уравнение относительно угловой скорости Ω при пуске на первом участке

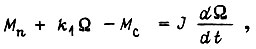
на втором участке

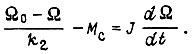
Здесь не учтена электромагнитная инерционность двигателя. Через 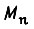обозначен пусковой момент, 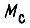- момент сопротивления, J - суммарный момент инерции привода. Будем считать, что при пуске и торможении 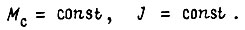Коэффициент k₁ равен

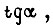
₂ определяем по формуле

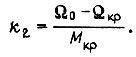
На первом участке

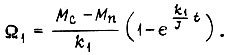
Пуск двигателя от скорости 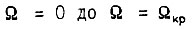происходит за время

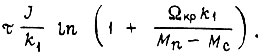
В вышеприведенных формулах под 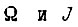понимаем скорость вращения вала двигателя и момент инерции, приведенный к валу этого двигателя.

На втором участке

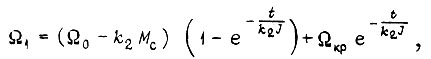
откуда видно, что 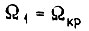при t = 0.

Функция 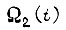в случае свободного выбега двигателя определяется уравнением

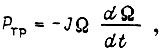
где 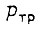- мощность потерь на трение. Аппроксимируя истинную 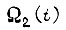убывающей экспонентой с постоянной времени 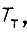получаем

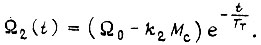
При динамическом торможении асинхронного двигателя функцию 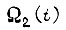можно представить аналогично 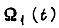на двух участках. Учитывая формулы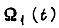 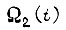и булевы функции, реализуемые логическими схемами, изображенными на рис. 82, 83, запишем в смешанной форме скорость вращения вала каждого двигателя:

рис. 82, двигатель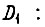

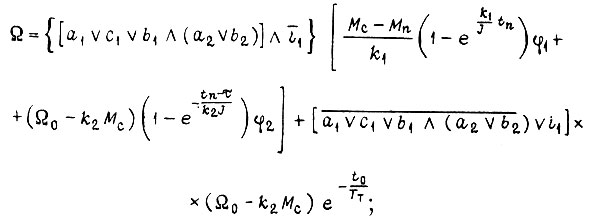
рис. 82, двигатель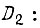

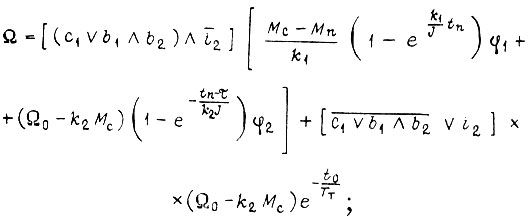
рис. 83, двигатель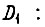

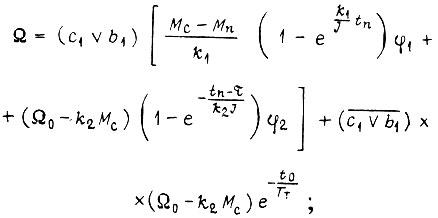
рис. 83, двигатель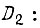

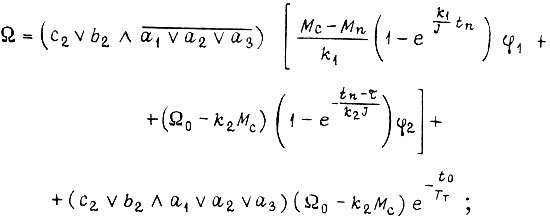
рис. 83, двигатель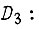

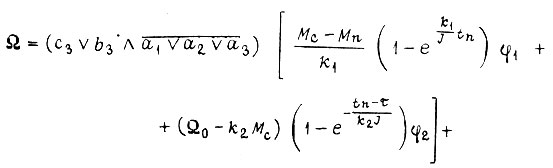
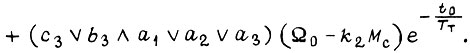
Здесь 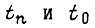- соответственно время, отсчитываемое после подачи команды на пуск двигателя, и время, отсчитываемое после подачи команды на остановку. Коэффициент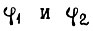ы равны

Формула для вычисления τ приведена выше. После выполнения операций алгебры Буля внутри скобок получаем либо булеву единицу, либо нуль. Затем следует операция умножения обычной алгебры, которой подвергаются десятичное число и результат логической операций (1 или 0). При этом булевы единица или нуль отождествляются с единицей или нулем обычной алгебры.

Рассмотрим систему привода робота с цикловым управлением, непрерывно переходящую из одних состояний 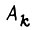в другие.

Для асинхронного электродвигателя такой системы формулу скорости вращения 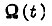при 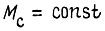можно записать в виде

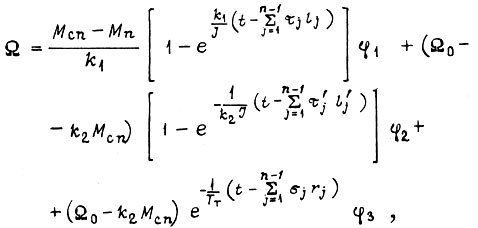
где 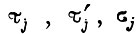- отрезки времени 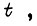отсчитываемые до подачи очередной команды на пуск двигателя. Коэффициенты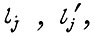 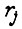принимают единичное либо нулевое значение в заданные моменты времени:

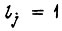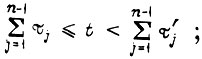
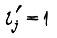при

при 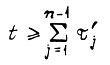и до окончания пуска;

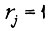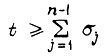при и до окончания торможения.

Величина 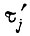рассчитывается по формуле

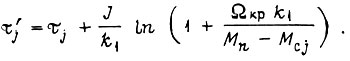
При каждом 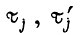либо 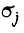имеем свое постоянное значение момента 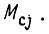Коэффициенты 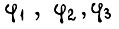есть булевы функции

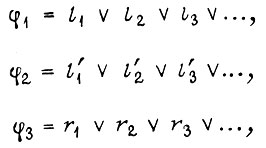
причем при использовании в формуле коэффициентов 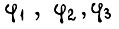единичные и нулевые значения их как булевых функций отождествляются с такими же значениями в обычной алгебре. Если известны булевы функции, реализуемые логической схемой системы привода, то можно вычислить частость пусков и торможений каждого двигателя, что важно знать при выборе мощности двигателей во время проектирования системы.

Если отождествлять частость включения какого-либо вида с вероятностью появления команды на такое включение на входе силового преобразователя, управляющего двигателем, то это означает, что вместо частости необходимо вычислять вероятность истинности булевой функции, реализуемой логической схемой на рассматриваемом выходе. Вероятность истинности подсчитывается по формуле 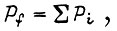где сумма берется по вероятностям тех наборов двоичных аргументов, для которых данная функция f обращается в единицу. Для вычисления 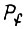функция f записывается в СДНФ.

Примеры СДНФ - совершенной дизъюнктивной нормальной формы функций:

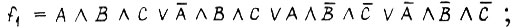
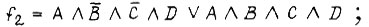
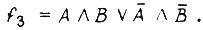
Пусть, например, требуется найти вероятность истинной функции 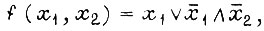если вероятности появления единичных значений 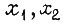равны соответственно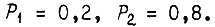

Записываем 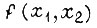в СДНФ:

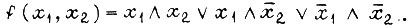
В полученной формуле заменяем 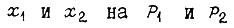соответственно. Преобразованная сумма равна искомой вероятности

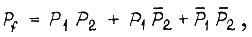
где 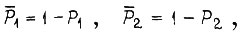в результате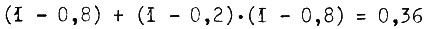

При переходе от 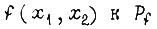операции логического сложения и умножения заменены на операции сложения и умножения десятичной алгебры.