2. О булевых функциях

Функция 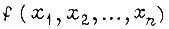называется булевой, если она, так же как и ее аргументы, может принимать только два значения: 0 и 1. С помощью булевой функции можно представить сигнал на любом выходе логической схемы, поскольку он определяется комбинацией входных сигналов 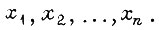Совокупность конкретных значений всех аргументов функции называют набором. Для краткости набор можно записывать в виде двоичного числа, например но при 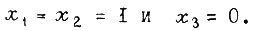Количество различных наборов конечно и зависит от числа аргументов. В общем случае функция n двоичных переменных определена в 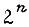наборах. Количество всех булевых функций N при n переменных равно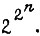

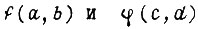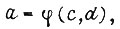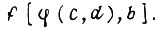Подстановка в функцию вместо ее аргументов других функций называется суперпозицией. Имея две булевы функции от двух переменных можно образовать функцию от трех переменных с помощью подстановки т. е. В алгебре Буля важную роль играют функции одной и двух переменных, из которых, используя принцип суперпозиции, строим любые булевы функции от любого числа переменных.

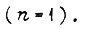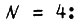
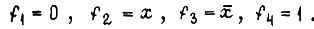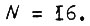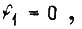
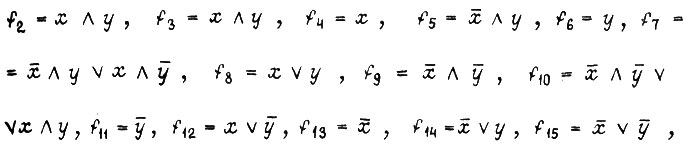
Наиболее простое выражение имеют булевы функции одного аргумента В этом случае число различных функций Функции двух аргументов определены в четырех наборах и Это следующие функции: 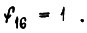Функции 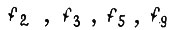называют конституентами единицы, они принимают значение, обозначенное единицей, только на одном наборе. По аналогии 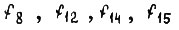- конституенты нуля.

Применяя булеву алгебру для проектирования логических схем, желательно иметь первоначальное представление функций в так называемой совершенной нормальной форме. Таких форм две. Совершенная дизъюнктивная нормальная форма (СДНФ) функции есть эквивалентное ее представление в виде дизъюнкции конституент единицы. Совершенная конъюнктивная нормальная форма (СКНФ) функции есть эквивалентное ее представление в виде конъюнкции конституент нуля. Эти формы функции могут быть получены последовательным применением известной теоремы разложения соответственно в ее первой и второй формулировках.

Для выполнения логического синтеза систем управления двигателями необходимо располагать информацией об операциях, выполняемых системой привода. Вначале составляют табличное представление каждой функции. Таблица содержит всевозможные комбинации значений переменных (наборы), где обычно переменные без отрицания обозначают символом 1, а с отрицанием - символом 0. В одной из колонок указывают значения функции при каждом наборе. По заданному табличному представлению функции можно получить алгебраическое выражение функции в виде СДНФ и СШ.

Пусть задана табличная форма функции:

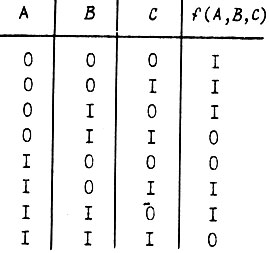
Представление функции в совершенной дизъюнктивной нормальной форме на основе табличной

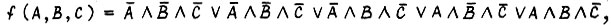
в совершенной конъюнктивной нормальной форме

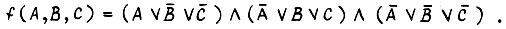
В первом случае имеет пять слагаемых, так как в пяти наборах f принимает значение, обозначенное единицей. Переменные 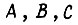в каждом слагаемом берутся без отрицаний, если в наборе, соответствующему этому слагаемому, эти переменные принимали единичное значение. В противном случае 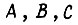берутся с отрицаниями. Во втором случае имеем три конъюнктивных члена, так как в трех наборах 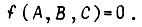Каждая переменная в каждом конъюнктивном члене берется с отрицанием, если в соответствующем наборе она принимает единичное значение, и без отрицания, если значение обозначено нулем.