3. Упрощение логических формул и схем

При построении логической схемы по заданной булевой функции с целью получения схемы, содержащей возможно меньшее число элементов, производят операцию минимизации исходной функции. В результате приходят обычно к формуле, имеющей уменьшенную длину.

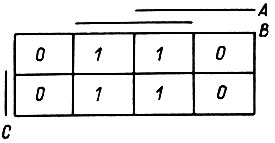
Рис. 86

Одним из приемов упрощения булевых функций, заданных в СДНФ, является применение диаграмм Карно. Пример диаграммы функции трех переменных 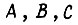приведен на рис. 86. Здесь изображена функция

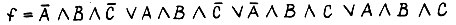
четырьмя квадратами с внесенными в них единицами,соответствующими четырем дизъюнктивным членам. Чтобы определить, какому квадрату соответствует каждое слагаемое, надо иметь в виду,что все квадраты, расположенные под линией (например, A или B) или справа от линии (C), представляют составляющие СДНФ, содержащие переменную без отрицания, обозначающую эту линию. Те слагаемые, которые не представлены в функции f, изображаются квадратами с внесенными в них нулями. Два квадрата, расположенные симметрично относительно осевой линии или рядом в одной строке или колонке,являются соседними, т. е. изображают слагаемые, различающиеся только одной переменной, например 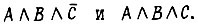Такие слагаемые можно заменить одним слагаемым, в которое будут входить в виде конъюнктивных составляющих только те переменные с отрицанием или без отрицания, которые представлены и в том и в другом слагаемом. Это соответствует операции

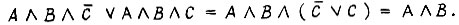
На рис. 86 четыре квадрата являются соседними; заменив их одним слагаемым, получаем

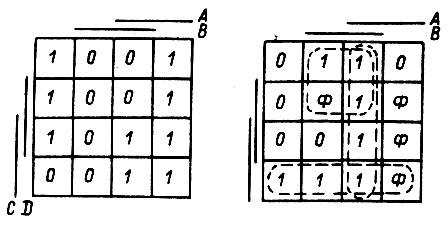
Рис. 87

На рис. 87 представлены две диаграммы для функций четырех переменных. Левая диаграмма изображает функцию

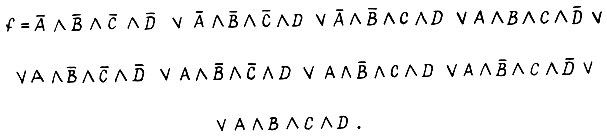
Учитывая понятие соседних наборов и пользуясь правилом их замены, получаем

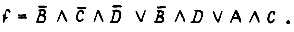
На правой диаграмме (рис. 87) в часть квадратов внесен индекс Φ, указывающий на то, что в наборах для данных квадратов функция не определена. Дело в том, что проектирование схемы обычно начинают с составления перечня всех возможных комбинаций входных сигналов. Если известно, что при работе схемы некоторые комбинации значений входных сигналов никогда не встречаются, то функция является недоопределенной. В целях минимизации функции можно произвольно ее доопределить, заменив Φ единицей или нулем так, чтобы образовались соседние наборы. Заполнив на рис. 87 в контурах, обведенных пунктирной линией, неопределенные квадраты единицами, получаем минимальную форму функции

На рис. 88 представлены диаграммы для функций пяти и шести переменных. После замены соседних наборов получаем соответственно минимальные формы

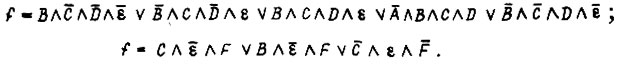
Для диаграмм на рис. 86 соседними являются квадраты, расположенные симметрично относительно любой четной линии, а также расположенные рядом по вертикали или горизонтали. Получение минимальных форм функций с помощью диаграмм Карно существенно усложняется при числе переменных более шести. Одним из методов, построенных на определенной процедуре алгебраических преобразований, является метод Квайна, в котором используются закон склеивания 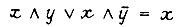и закон поглощения 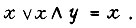Те же законы для функций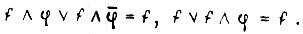

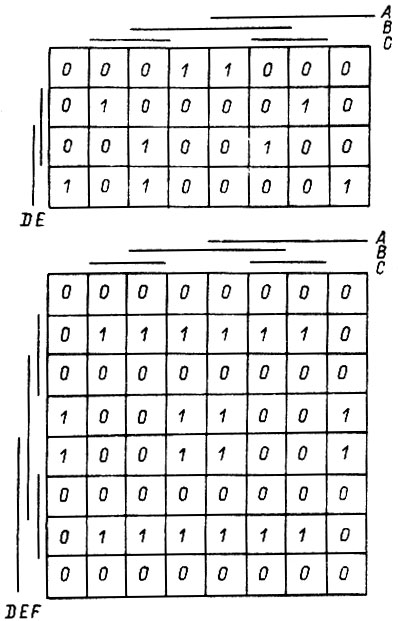
Рис. 88

Функция φ называется импликантой функции f; если во всех точках, где φ равна единице, функция f тоже равна единице. Если эти функции представлены таблицами с одинаковым порядком размещения наборов, то при наложении таблиц все единицы функции φ совпадут с частью единиц функции f, а все нули функции f совпадут с частью нулей функции φ. Простой, импликантой функции f называется элементарная конъюнкция 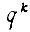k-го ранга 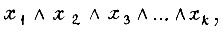если она является импликантой f, но никакая часть этой конъюнкции, полученная вычеркиванием любых букв, не является импликантой f. Элементарные конъюнкции k-го ранга 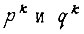называются соседними, если они отличаются только тем, что одна из переменных входит в 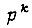с отрицанием, а 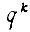без отрицания. Если конъюнкция не имеет ни одной соседней среди заданного множества элементарных конъюнкий k-го ранга, то такую конъюнкцию называют изолированной. Очевидно, что дизъюнкция двух соседних элементарных конъюнкций k-го ранга есть элементарная конъюнкция 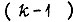-го ранга. Квайном показано, что минимальная форма функции f есть дизъюнкция некоторых простых импликант функции f. Первоначально минимизируемая функция должна быть задана в СДНФ. Сущность метода заключается в отборе для каждой конъюнкции n-го ранга всех соседних и в применении операции склеивания в каждой паре соседних конъюнкций. При этом получается множество конъюнкций 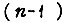-го ранга, изолированные конъюнкции n-го ранга, к которым не применима операция склеивания, являются простыми импликантами функции. Конъюнкции, к которым применена операция склеивания, исключаются из дальнейшего рассмотрения. Эта процедура склеивания применяется далее к сформированной новой группе элементарных конъюнкций 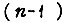-го ранга. Изолированные конъюнкции 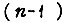-го ранга тоже являются простыми импликантами. Получаем конъюнкции 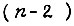-го ранга. Процедура склеивания и исключения "склеенных" конъюнкций продолжается до тех пор, пока не останется ни одной пары конъюнкций, для которых она применима. Любой член может участвовать в операции склеивания любое число раз. В результате получим ряд простых импликант.

Дизъюнкция всех простых импликант в общем случае содержит избыточные члены, т. е. не является минимальной формой функции. Здесь еще отдельные простые импликанты могут поглощаться дизъюнкцией оставшихся. Последовательно пользуясь законом поглощения для каждой простой импликанты, получим, так называемую тупиковую или неизбыточную форму функции. Булева функция может иметь несколько тупиковых форм. Для определения минимальной формы функции, содержащейся во множестве тупиковых, необходим перебор последних.

Рассмотрим упрощение формульного представления булевой функции методом Квайна на примере. Задана функция 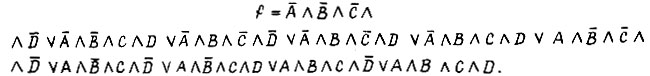Применяя операцию склеивания, имеем следующие ряды конъюнкции четвертого, третьего и второго рангов:

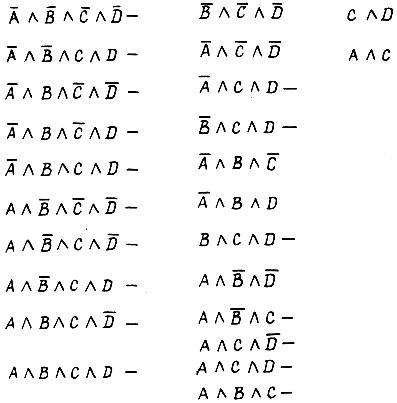
Элементарные конъюнкции, подвергнутые операции склеивания, отмечаются знаком - . Все неотмеченные конъюнкции являются простыми импликантами. Итак, получена форма функции

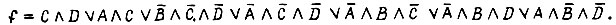
Составим импликантную таблицу:

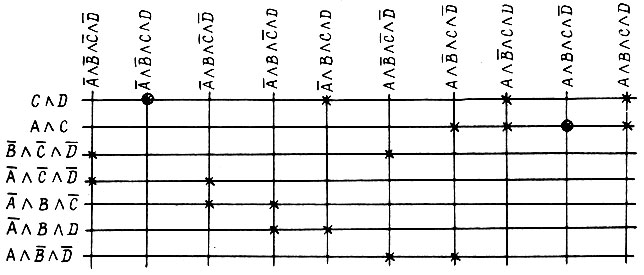
Конституэнты 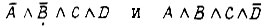имеют по одной метке. Импликанты в строках которых есть эти метки, называются существенными простыми импликантами (СПИ). Существенные простые импликанты обладают тем свойством, что каждая из них представляет хотя бы один член СДНФ, не поглощаемый никакой другой простой импликантой. Дизъюнкция всех СПИ составляет так называемое ядро заданной функции. Это ядро должно входить в каждую тупиковую форму функции. Теперь исключаем из таблицы все конъюнкции СДНФ, поглощаемые а также сами СПИ:

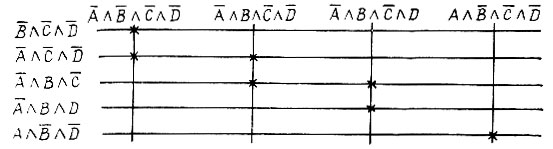
Каждая из следующих совокупностей простых импликант имеет хотя бы одну метку в каждой колонке таблицы:

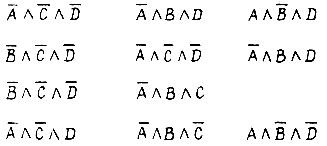
Итак, заданная функция имеет четыре тупиковые формы:

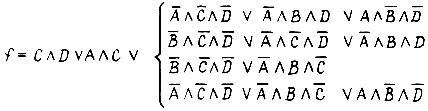
Очевидно, минимальная форма функции есть

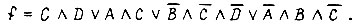
Применяя метод Квайна, диаграммы Карно, а также другие известные методы (Мак-Класки, Харриса и т.д.) для минимизации булевых функций, мы получаем формулы минимальной длины. Для изготовления схемы с наименьшим числом элементов необходимо знать номенклатуру и свойства элементов выбранной серии. Пользуясь различными частями серии, можно получить и различное количество элементов для реализации одной и той же функции.

В ряде случаев может оказаться, что вынесение общих множителей внутри минимальной формы функции приводит к сокращению требуемого оборудования. При проектировании комбинационных схем со многими выходами может стать целесообразным при реализации данной функции f так строить схему, чтобы в ее состав входило оборудование, реализующее другую заданную функцию φ. Такого рода задачи проектирования сводятся, как правило, к отысканию и минимизации решений булевых уравнений. Булево уравнение имеет следующий общий вид:

где 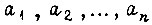- двоичные переменные; 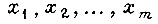- некоторые булевы функции от 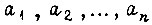, подстановка которых в уравнение обращает последнее в тождество. Решение уравнения заключается в отыскании функций

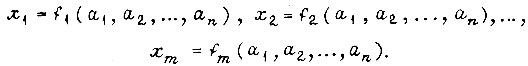
Пусть задана логическая схема, показанная на рис. 89, где для первого выхода 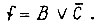Требуется дополнить схему так, чтобы была реализована функция второго выхода 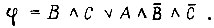Задача сводится к решению уравнения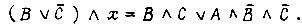

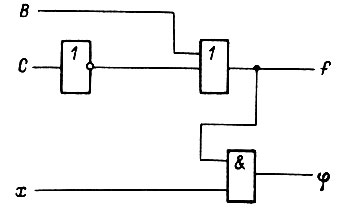
Рис. 89

Построим таблицу всех возможных наборов двоичных переменных 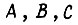, в которой укажем значения функций 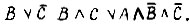Затем подберем в каждой строке таблицы (для каждого набора) такое значение x, которое удовлетворяет уравнению. В тех строках, где любое значение x удовлетворяет уравнению (1 или 0), употребим для x символ 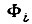где i - номер набора переменных.

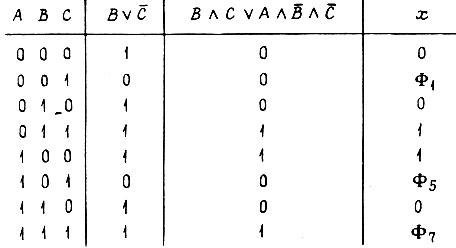
Решение уравнения о СДНФ

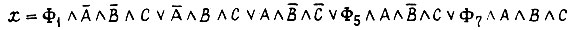
Подставляя всевозможные комбинации значени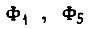й и 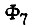(1 или 0), получаем восемь решений. Если 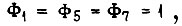то получаем наиболее простое решение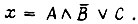

Булевы уравнения с двумя неизвестными x, y можно решить аналогично, применив табличный способ. В результате имеем при трех переменных 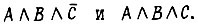совокупность функций 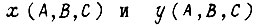в СДНФ. К решению булевых уравнений сводятся также задачи построения последовательностных логических схем, содержащих элементы памяти.