4. Построение последовательностных логических схем

Состояние системы привода, содержащей последовательностную логическую схему, определяется в каждый момент времени не только входной комбинацией сигналов последовательностной схемы, не и предысторией ее переключений.

Рассмотрим метод построения последовательностной логической схемы на элементах,реализующих операции конъюнкции, дизъюнкции и инверсии. Сущность метода состоит в определении количества и размещения состояний промежуточных переменных путем построения и последующей минимизации таблицы переходов состояний схемы. При этом синтез логической схемы делится на несколько этапов.

На первом этапе строится первичная таблица переходов на основании условий работы схемы, заданных, например, в виде последовательности сигналов: входной:

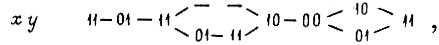
выходной:

Построим таблицу переходов.

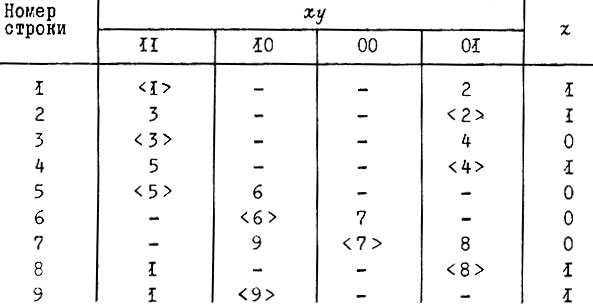
Входными сигналами схемы являются x и y, выходным - z. Каждое состояние будущей схемы, заданное последовательностями изменения x, y и z, пронумеровано. Процесс переключения схемы содержит 9 состояний. Эти состояния назовем устойчивыми. Каждому устойчивому состоянию схемы соответствует одна строка таблицы. Устойчивые состояния в таблице переходов заключаются в угловые скобки. Например, 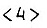- четвертое устойчивое состояние, 5 - пятое неустойчивое состояние. При изменении состояния входов в первую очередь рассматриваются переход вдоль строки от предшествующего устойчивого состояния к неустойчивому состоянию, соответствующему новой комбинации значений сигналов на входах, а затем вдоль столбца к новому устойчивому состоянию схемы. Таким образом, всякий переход из одного устойчивого состояния в другое происходит по меньшей мере черед одно неустойчивое состояние. Продолжительность неустойчивого состояния определяется временем запаздывания в передаче воздействия на выход схемы и зависит от физических свойств и количества последовательно включенных элементов.

На втором этапе минимизируют таблицу путем совмещения строк. Совмещение можно проводить для двух и большего числа строк, имея в виду следующее:

1. если в каждом столбцов сравниваемых строк номера состояний одинаковы или в одной из строк имеются прочерки, то данные строки могут быть совмещены в одну;
2. если среди объединенных номеров состояний одно является устойчивым, а другое нет, то в совмещенной строке проставляется устойчивое состояние.

Рассмотрим совмещение строк в таблице для нашего примера. Из сопоставления строк видно, что можно совместить строки 4, 5 и 6; 7, 8 и 9; 1 и 6; 1 и 9. При любом варианте совмещения строки 1 с другими строками, так же как и при отказе от ее совмещения, число строк после совмещения не увеличивается, так как строки 6 и 9 входят в другие группы. Поэтому следует искать другие признаки для их учета при совмещении строк. Одним из таких признаков является сохранение после совмещения возможно большего числа прочерков в строках таблицы. Прочеркнутые клетки, соответствующие неиспользуемым состояниям, используются в дальнейшем для упрощения выражений промежуточных переменных. Строка 1 имеет прочерки во втором и третьем столбцах, но при любом варианте совмещения их число уменьшается. Поэтому объединять строку 1 ни со строкой 6, ни со строкой 9 не следует. Итак, принимаем вариант, при котором строки совмещаются в группы 4, 5, 6 и 7, 8, 9. Выпишем эти группы отдельно:

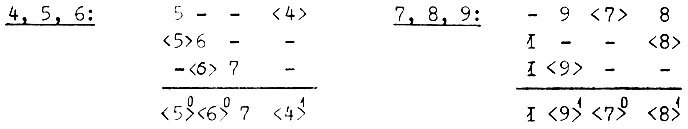
Так как состояния выхода у совмещаемых строк различны, то около каждого устойчивого состояния в совмещенной строке проставляются соответствующие им значения выходов например 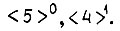Полученная в результате совмещения строк таблица переходов содержит уже пять строк:

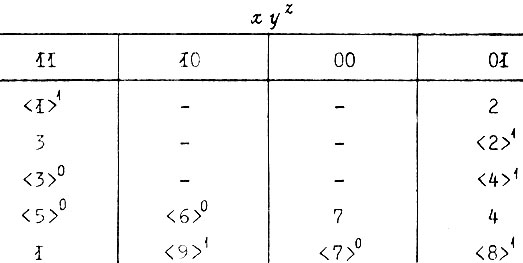
Далее выявляют в таблице эквивалентные состояния, характеризующиеся следующими особенностями:

• они находятся в одном столбце таблицы переходов и имеют одинаковые значения выходов;
• одной и той же последовательности входных сигналов для этих состояний соответствуют одинаковые последовательности изменения выходов.

В полученной таблице переход от состояния 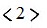к состоянию 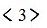и от состояния 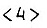к состоянию 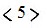сопровождается изменением выхода с 1 на 0. Этот переход возможен в том случае, если после комбинации 01 на входы будет подана комбинация 11. Таким образом, состояния (а точнее говоря, пары состоян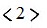ий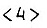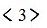) и , и 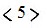удовлетворяют признакам эквивалентных состояний.

При обнаружении эквивалентных состояний состояния с большими порядковыми номерами следует заменить соответствующими им состояниями с меньшими номерами, а лишние строки из таблицы переходов исключить. В данном случае из таблицы исключаются вторая и третья строки, а в четвертой строке состояние 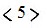заменяется состояние 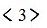, а состояние 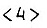- состоянием 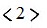. Итак, получаем вторичную таблицу переходов:

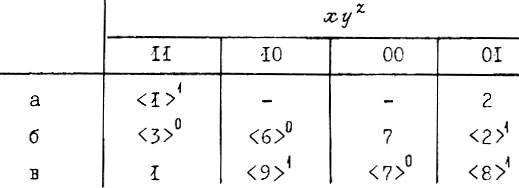
На третьем этапе определяют количество и размещают состояния промежуточных переменных. Минимальное количество промежуточных переменных определяется по формул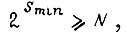е где 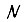- число строк во вторичной таблице переходов; 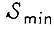- минимально необходимое количество промежуточных переменных, имеющих два устойчивых состояния.

Каждой строке вторичной таблицы переходов необходимо поставить в соответствие определенную комбинацию значений промежуточных переменных с тем, чтобы строки различались между собой как минимум значением одной переменной. От качества выполнения этой операции зависит сложность логической схемы. Необходимо также учитывать, что передача сигналов между элементами, схемы может происходить либо синхронно, либо несинхронно. В первом случае передача сигналов происходит синхронно с изменением напряжения питания логических элементов и без затухания. При этом не возникают такие нежелательные явления, как состязания элементов. Внимание проектировщика должно быть направлено на получение размещения, не допускающего возникновения недопустимых состязаний, нарушающих заданный режим переключений. Под состязанием понимается режим, при котором либо одновременно изменяют свое состояние несколько промежуточных переменных, либо переключаются цепи удержания для некоторой промежуточной переменной. При допустимых состязаниях схема в результате нескольких переходов все же приходит в заданное устойчивое состояние, а при недопустимых нарушается ее функционирование.

Обозначим строки вторичной таблицы переходов через а, б, в. Для двух промежуточных переменных возможна последовательность соседних состояний, т. е. состояний, отличающихся друг от друга значением только одной промежуточной переменной: 11, 10, 00, 01. Поставим в соответствие начальной строке вторичной таблицы переходов, содержащей состояние 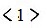, нулевую комбинацию переменных. При этом возможны следующие шесть вариантов размещения комбинаций:

Варианты 1-5, 2-6, 3-4 равноценны, поэтому рассмотрим варианты 1, 2 и 3. В варианте 1 две промежуточные переменные переходят с 1 на 0, но такой переход обычно не вызывает недопустимых состязаний. В варианте 2 при изменении двух переменных с 0 на 1 состязание, вообще говоря, не исключено. В варианте 3 при переходе от комбинации 10 к 01 недопустимое состязание происходит почти всегда. Первый вариант наиболее предпочтителен. Результаты размещения заносятся в отдельную таблицу:

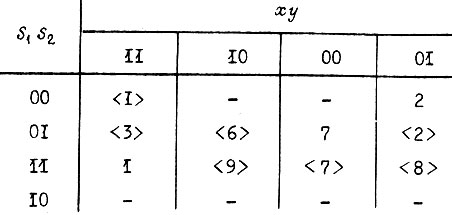
На четвертом этапе переходят к построению диаграмм Карно для функций 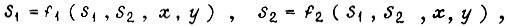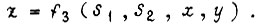Диаграммы строят таким образом, что ее столбцам соответствуют комбинации входных переменных, а строкам - комбинации промежуточных. Диаграмма Карно для каждой функции отличается от вторичной таблицы переходов либо порядком расположения столбцов, либо строк и тем, что вместо номеров устойчивых состояний в клетки диаграммы заносятся значения искомой функции, поставленные в соответствие данным устойчивым состояниям (а для z - значения, известные из условия задачи). Вместо номера неустойчивого состояния в клетку диаграммы проставляется значение функции то же, что и для устойчивого состояния, имеющего одинаковый номер. Черта каждой переменной перекрывает те столбцы или те строки диаграммы Карно, для которых эта переменная эквивалентна единице. Учитывая таблицу с комбинациями значений 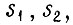а также вторичную таблицу переходов, получаем диаграммы Карно.

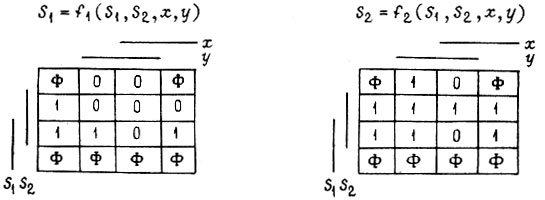
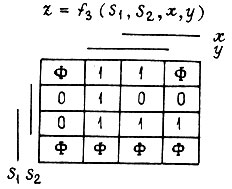
Все прочерки в таблице заменены в клетках диаграмм Карно индексами Φ, указывающими на произвольность значения булевой функции. В рассматриваемом, случае в диаграмме для 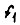заменяем все Φ на 0, а в диаграммах для 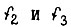- все Φ на 1. Тогда получаем минимальные формы функций

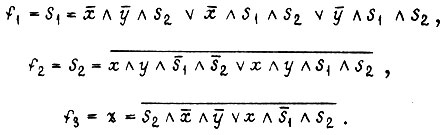
Логическая схема, реализующая заданную последовательность изменения сигнала z, изображена на рис. 90.

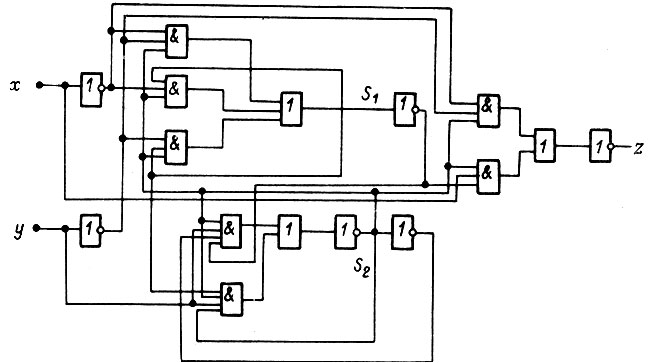
Рис. 90

Для получения неразрывных значений функций во время перехода от одного устойчивого состояния к другому при несинхронной передаче сигналов между элементами необходимо, чтобы те клетки диаграммы, между которыми происходят переходы, имели хотя бы одну общую клетку с тем же значением функции или были бы связаны объединением, имеющим общие клетки с двумя первыми.

Иным является подход к построению последовательностной схемы с использованием элементов памяти. Рассмотрим построение последовательностной схемы с произвольно заданной программой переключений состояний их выходов.

Пусть логическая схема имеет p входов, q выходов и r элементов памяти. Обозначим через 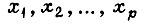сигналы на входах схемы, 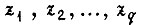- сигналы на выходах, 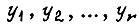состояние элементов памяти. В любой момент времени состояние всех выходов 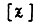определяется совокупностью состояний входов 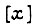и внутренним состоянием схемы 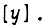Для n-го такта эту связь можно выразить так: 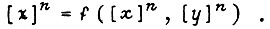Здесь n обозначает такт. Для i-го выхода схемы

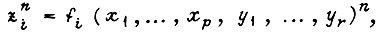
где 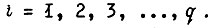Совокупность состояний элементов памяти в последующем 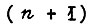-м такте 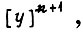в свою очередь, определяется входными и внутренними состояниями в момент предыдущего n-го такта:

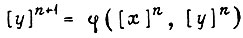
или для j-го элемента памяти

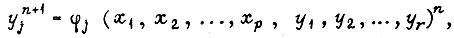
где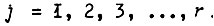

Процессы переключения в схеме описываются с помощью системы уравнений

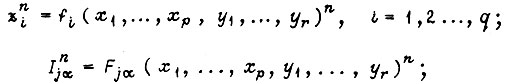
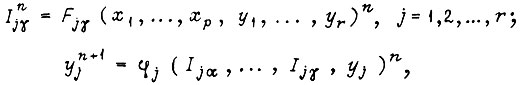
где - входы j-го элемента памяти. Последнее уравнение есть собственное уравнение j-го триггера и записывается различным образом для триггеров типов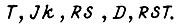

Рассмотрим построение последовательностной схемы, которое сводится к выделению комбинационной части. Пусть требуется построить схему на трех T-триггерах, выходы которых 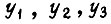последовательно принимают состояния от такта к такту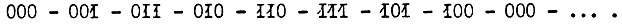

Предположим, что в схеме имеется один вход x, на котором в начале каждого такта появляется узкий импульс 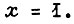С приходом этого импульса начинается переключение триггеров. Построим таблицу, в которой укажем состояния T-триггеров в n-м и 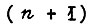-м тактах, пользуясь условием задачи.

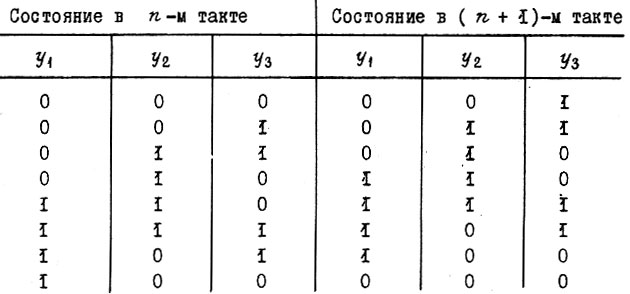
Из таблицы получаем в СДНФ три функции:

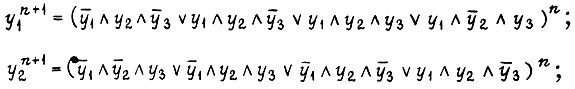
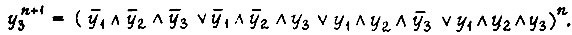
Полученные выражения преобразуются следующим образом:

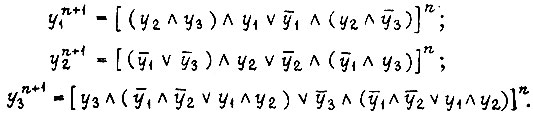
В общем виде каждое из этих уравнений можно записать так:

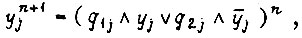
где 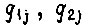- булевы функции, не зависящие от той переменной, для которой написано уравнение. Перепишем выражение 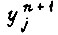вместе о уравнением T-триггера, характеризующим его свойства:

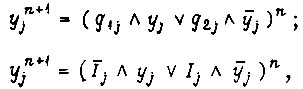
где 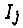- входной сигнал элемента памяти.

Из эквивалентности левых частей двух уравнений получаем эквивалентность правых частей, справедливую для любого такта:

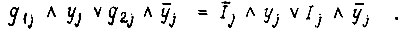
Решим данное уравнение относительно 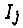табличным способом. Независимыми переменными здесь являются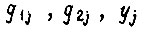

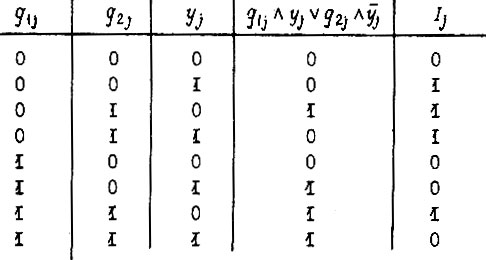
Для всех возможных наборов этих переменных определим значения левой части уравнения, а затем подберем такое значение 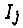для каждого набора, при котором уравнение обращается в тождество. На основании этой таблицы представляет 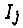в СДНФ как булеву функцию: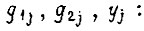

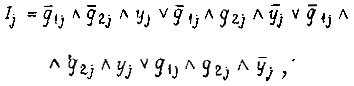
после упрощения

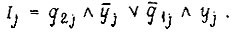
Это - общее уравнение для выходного сигнала каждого из трех T-триггеров схемы.

Учитывая, что

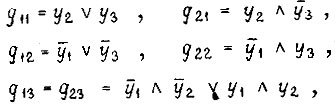
получаем после подстановки в уравнение 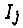и последующего преобразования

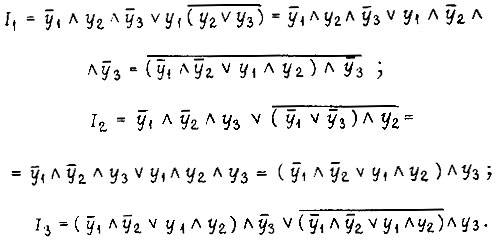
На рис. 91 изображена комбинационная часть схемы вместе с элементами памяти 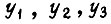. Смена состояний схемы удовлетворяет условию задачи.

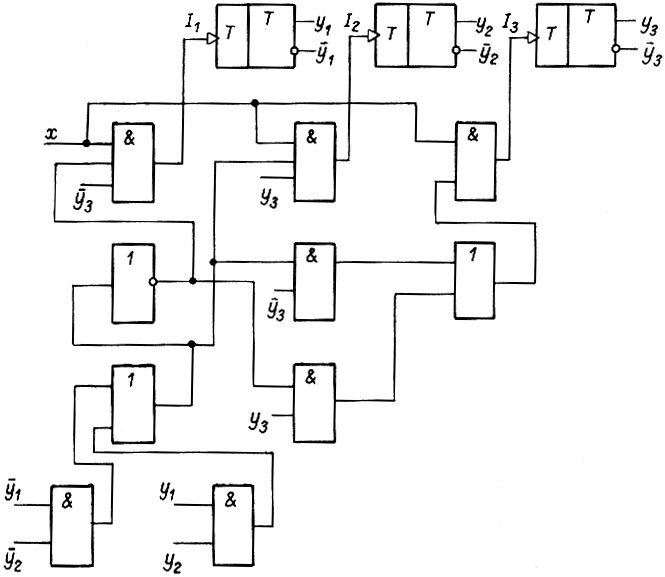
Рис. 91

Построим логическую схему для того же условия задачи, а с использованием 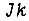-триггеров. Собственное уравнение этого триггера для выходных сигналов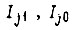

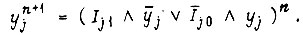
Рассматривая теперь, как и для T-триггеров, аналогичную систему уравнений

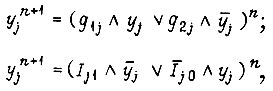
получаем для любого такта

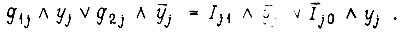
Это уравнение может быть решено табличным способом. Однако из записи уравнения следует, что оно обращается в тождество, если 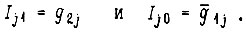Это и есть одно и решений, которое принимаем, учитывая его простоту. В результате 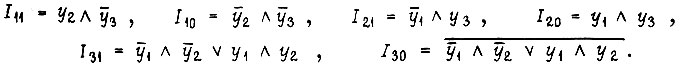Комбинационная часть схемы вместе с тремя 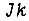-триггерами изображена на рис. 92. На входы элементов умножения, расположенных непосредственно перед входами триггеров, поступают сигналы, найденные путем решения поставленной задачи, а также сигнал входа x (как и на рис. 91). Переключение триггеров производится каждый раз, когда 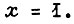Длительность сигнала 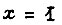не должна превышать длительности внутренней задержки каждого из 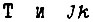-триггеров. При отсутствии элементов задержки схемы (см. рис. 91, 92) могут оказаться неработоспособными.

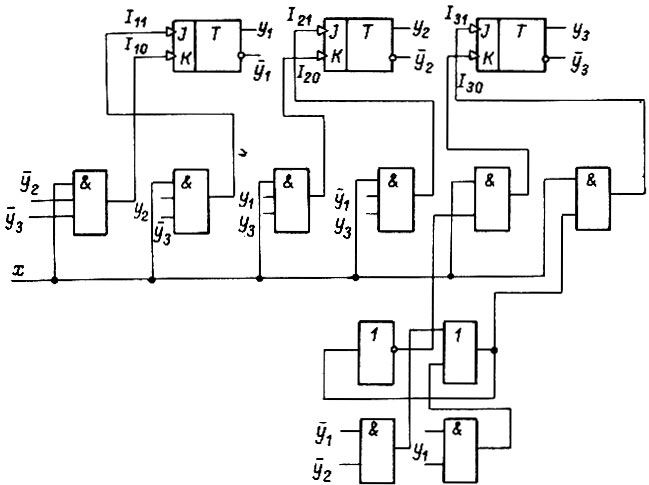
Рис. 92

Для построения комбинационной части последовательностной схемы, содержащей 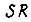-триггеры, необходимо решить систему уравнений

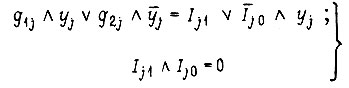
либо

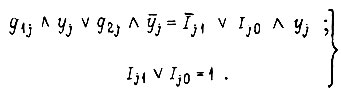
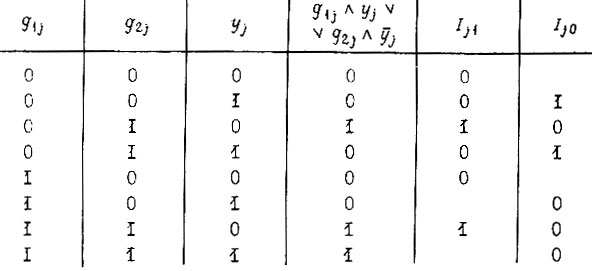
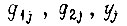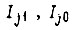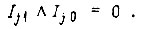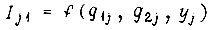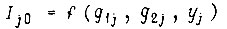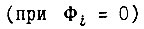
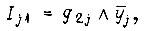
Решим только первую систему. Для этого построим таблицу, в которой для каждого набора подберем такие комбинации значений для которых удовлетворяется условие Исследовав функции и c помощью диаграмм Карно, получаем минимальные формы искомых функций 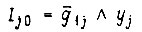Для сформулированной выше той же задачи построения последовательноетной схемы имеем следующие формулы входных сигналов 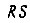-триггеров:

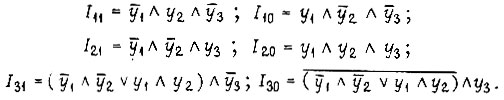
На рис. 93 изображена логическая схема, построенная 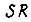-триггерах с двухступенчатым запоминанием информации.

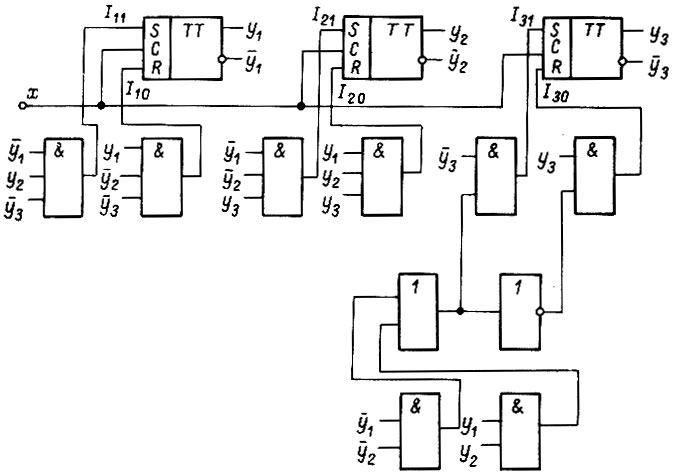
Рис. 93

Используя 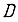-триггеры для решения той же задачи, получаем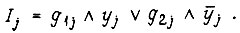

Для каждого 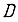-триггера

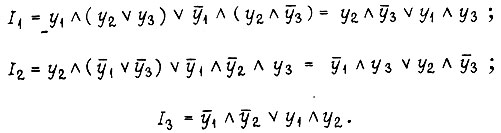
Схема, содержащая 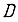-триггеры с двухступенчатым запоминанием информации, изображена на рис. 94.

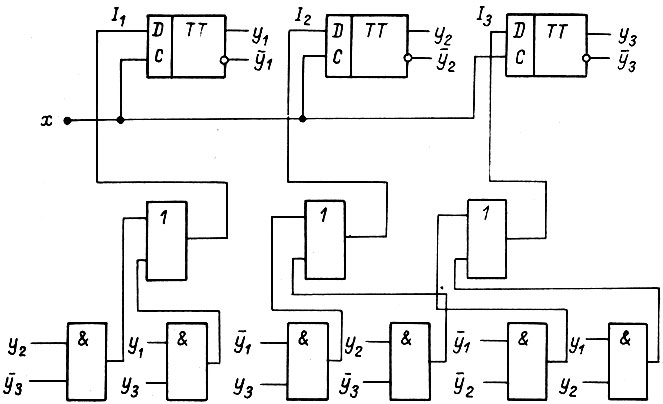
Рис. 94

Для построения схемы с использованием 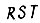-триггеров необходимо решить систему уравнений

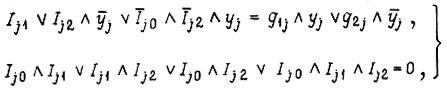
где 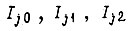- входные сигналы триггера. Решение данной системы уравнений сводится к табличному решению первого уравнения, где для каждого набора 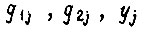подбирается такая комбинация значений 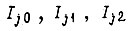, для которой второе уравнение обращается в тождество. Для минимизации решения, получаемого в общей форме и содержащего факультативные значения 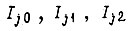, необходимо применение диаграмм Карно.