3.3. Основы газодинамики

В качестве рабочего тела в пневмоприводах используется газ - сжатый воздух. Основными характеристиками состояния газа являются: абсолютное давление р, плотность газа ρ и абсолютная, температура Т. В дальнейшем для простоты расчетов принимается, что состоянием рабочего тела в пневмоприводах является состояние идеального газа, которое описывается уравнением Клапейрона:

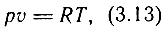
где υ = V/m; V - объем газа; m - масса газов объема V; R - газовая постоянная, для воздуха R = 287,14 Дж/(кг⋅К). Отсюда

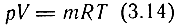
или

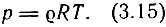
Ниже приведены частные случаи уравнения состояния.

Особенности процессов в пневмоприводах. При рассмотрении основных термодинамических процессов в полостях пневмоприводов принимается, что имеют место равновесные процессы, т. е. процессы, при которых температура и давление одинаковы в рассматриваемом объеме.

Процесс, протекающий без теплообмена с окружающей средой, называется адиабатным. При этом внешняя работа газа совершается за счет изменения объема; при расширении газа температура его снижается, при сжатии - повышается. Зависимость между параметрами газа в данном процессе выражается уравнением

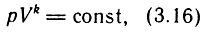
называемым адиабатой.

Показатель адиабаты k определяется как отношение теплоемкостей газа при постоянном давлении с_р и постоянном объеме c_v:

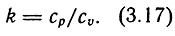
Для воздуха k = 1,4.

Из уравнения состояния газа с учетом зависимости (3.16) можно получить следующие соотношения параметров:

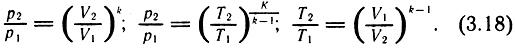
Для общего случая теплообмена с окружающей средой зависимость между параметрами газа может быть представлена выражением

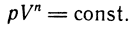
Это так называемый политропический процесс, где n - показатель политропы. Соотношения параметров аналогичны зависимости (3.18), при этом значение k заменяется значением n. Для изобарного процесса n = 0, для изотермного n = 1, для адиабатного n = k, для изохорного n = ∞.

Динамика потока газа. Для определения основных зависимостей при расчетах конструкций и динамики пневматических устройств рассмотрим режим течения газа, наиболее часто встречающийся на практике, - одномерное течение идеального газа без трения и теплообмена с окружающей средой (адиабатное течение).

Условия течения (рис. 3.8):

- на элемент потока действуют только силы давления;

- рассматриваемые сечения 1-1 и 2-2 элемента потока находятся на одном уровне.

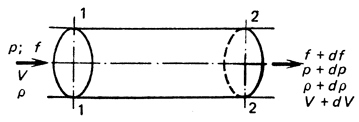
Рис. 3.8. Схема сил, действующих в потоке жидкости

Составим уравнения равновесия действующих сил.

1. Сила, действующая на элемент объема жидкости в направлении движения:

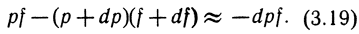
2. Изменение момента количества движения:

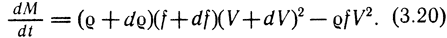
Упростим уравнение (3.20):

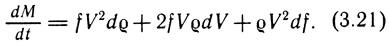
Зависимость (3.21) представляет собой полный дифференциал выражения ρfV. Таким образом,

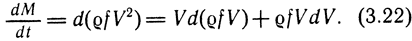
Из известного в гидродинамике закона непрерывности для газов следует, что в установившемся движении газа изменение массы в рассматриваемом неподвижном объеме не происходит. Следовательно, в объем втекает и из объема вытекает одинаковое количество массы жидкости.

Таким образом, для сечений 1-1 и 2-2

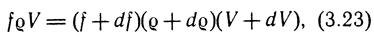
где fρV - единичный расход массы через сечение 1-1. Или

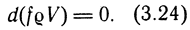
Подставим зависимость (3.24) в (3.22). Окончательно получим

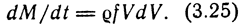
Уравнение равновесия сил элемента объема:

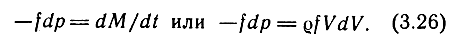
Преобразуем выражение (3.26):

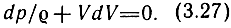
При этом получим уравнение Эйлера для одномерного потока сжимаемой жидкости (газа). Его решение запишется как

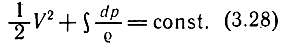
Интеграл может быть определен только в том случае, если известна зависимость между давлением и плотностью. Для адиабатного режима

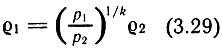
или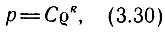

где С - константа;

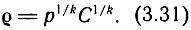
Решая совместно (3.28) и (3.31), найдем

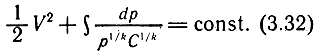
Для сечений 1-1 и 2-2 выражение (3.32) имеет значение

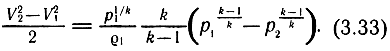
Выражение (3.33) определяет зависимость между скоростью потока сжимаемой жидкости и давлением без трения и теплообмена со стенками.

В реальных конструкциях пневматических устройств соотношение площадей каналов подвода и выхода газа таково, что можно принять V₁ = 0. Кроме того, длины участков пневматических каналов незначительны, а поэтому можно принять режим течения газа адиабатным. При этом потери энергии потока в конструкции устройств учитываются коэффициентом расхода μ; т. е. отношением реальной скорости к теоретической. С учетом принятых допущений скорость на срезе выходного отверстия

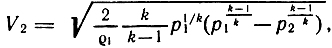
или

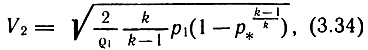
где р_* = р₂/р₁.

Массовый расход газа определяется зависимостью

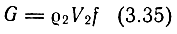
или с учетом принятых допущений (n = k; μ = 1) и зависимостей (3.34) и (3.29)

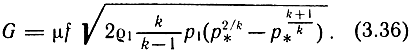
Но ρ = p/(RT), тогда (3.36) примет вид

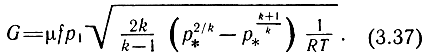
При рассмотрении конструкции и процессов пневмопривода используются следующие определения:

- рабочей полостью (полостью наполнения) называется подпоршневое пространство, в которое поступает сжатый газ из магистрали для совершения работы по перемещению поршня;

- выхлопной полостью (полостью опорожнения) называется камера привода, соединенная со средой, куда происходит выброс газа.

В процессе работы привода одна и та же полость может выполнять или функцию рабочей полости, или функцию выхлопной полости;

- рабочим циклом называется период работы привода, по истечении которого все исполнительные элементы занимают исходные позиции. Время рабочего цикла привода складывается из времени прямого хода рабочего органа и времени обратного хода.

При постоянных конструктивных параметрах пневматических устройств расход газа является функцией относительного давления. Исследование на минимум позволяет определить максимальный расход G_max при критическом отношении давлений:

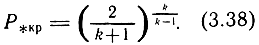
С учетом (3.38) зависимость (3.37) принимает вид

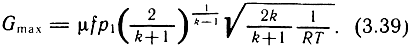
Выражение (3.39) определяет максимальное (или критическое) значение расхода в пневматических устройствах: при k = 1,4 (для воздуха) значение р_*кр = 0,5282. Зависимости (3.37) и (3.39) называются формулами Сен-Венана-Ванцеля.

Таким образом, при истечении газа из трубопровода могут быть два режима:

1) надкритический режим, при этом расход газа определяется зависимостью (3.39) и не меняется с изменением давления окружающей среды, т. е. при р_*кр = 0,5282 расход достигает максимума и равен G_max = const;

2) докритический режим, при этом расход газа определяется зависимостью (3.37) и величина расхода зависит от относительного давления.

Практика и расчеты показывают, что при скоростях газа, значительно меньших, чем скорость звука в жидкости, можно использовать в расчетах зависимости для несжимаемых жидкостей. Так, скорость звука в воздухе при комнатной температуре с = 320 м/с. Если скорость воздуха в реальной конструкции V = 60 м/с, т. е. V/c ≤ 0,2 (V/c - число Маха), то для определения расхода воздуха можно использовать зависимость

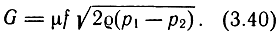
При расчетах расхода газа, проходящего через местное сужение потока, важно правильно определить коэффициент расхода μ. Он зависит как от конфигурации рассматриваемого местного сужения потока, так и от режима течения. Имеются справочники, в которых данные местные сужения потока систематизированы и приводятся зависимости для определения коэффициента μ.

Пользуясь зависимостями (3.26) и (3.28), можно сделать практический вывод: если в качестве рабочего тела привода использовать газ и подводить его к дросселю с постоянным давлением, постепенно уменьшая давление на выходе, то расход газа через дроссель будет увеличиваться до тех пор, пока отношение давлений выхода и входа Р_вых/Р_вх = р_* не достигнет критической величины; для воздуха p_*кр = 0,529. После этого дальнейшее уменьшение давления на выходе не влияет на течение газа. В этом случае скорость газа достигает максимального значения - скорости звука в жидкости (газе) 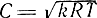для данных геометрических размеров сопла. Дальнейшего увеличения скорости газа можно достичь только путем создания специальных профилей сопла (сопло Лаваля). При этом можно получить сверхзвуковые скорости истечения. В практических расчетах пневматических устройств для определения расхода через дроссели с турбулентным режимом течения используют более простые формулы:

- докритическое истечение

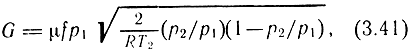
- надкритический режим

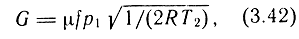
где принято (р₂/р₁)_кр = 0,5.