3.4. Статические и динамические характеристики привода

Пневматические исполнительные механизмы - устройства, преобразующие энергию сжатого газа в энергию перемещения выходного механического звена привода. В пневматических робототехнических устройствах в основном используют поршневые исполнительные механизмы, так как они конструктивно просты, надежны и обеспечивают значительное рабочее усилие.

Поршневой привод конструктивно можно выполнить в виде привода одно- или двустороннего действия (рис. 3.9).

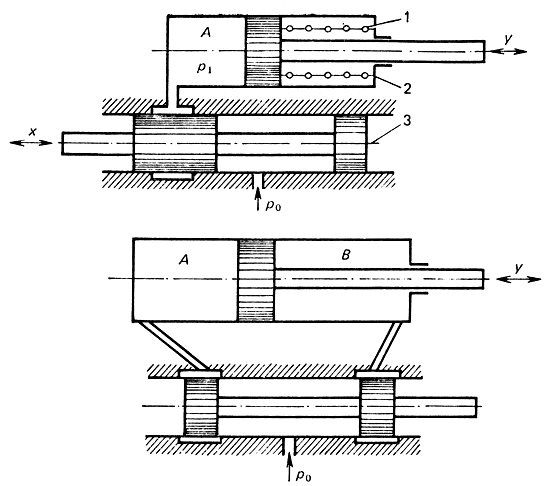
Рис. 3.9. Схема поршневого исполнительного двигателя: 1 - возвратная пружина; 2 - рабочий цилиндр; 3 - распределительное устройство

Воздух подается в рабочие полости цилиндра с помощью распределителя, в качестве которого используются конструкции цилиндрического золотника, плоского золотника, струйной трубки.

Усилие страгивания поршня из положения покоя определяется зависимостью

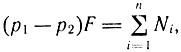
где р₁ - давление в полости нагнетания; р₂ - давление в полости опорожнения; F - площадь поршня; 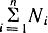- сумма сил, действующих на поршень.

Для определения уравнений динамики газа в полостях привода принимаются следующие допущения:

- проходные сечения цилиндра выполнены в виде дросселей с турбулентным режимом течения;

- процесс наполнения и опорожнения газа происходит в адиабатном режиме;

- режим течения, проходящего через дроссели, - квазистационарный.

Масса газа в рабочей полости цилиндра

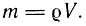
Дифференцируя данную зависимость по времени и используя уравнение для идеального газа р = ρRТ, получим

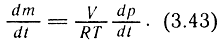
Данное изменение массы представляет собой массовый расход газа G, определяемый по известным зависимостям (3.37) и (3.39):

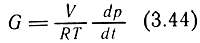
для докритического и надкритического режимов истечения газа, для воздуха - по зависимостям (3.41) и (3.43). После подстановки (3.41) и (3.42) в выражение (3.44) и интегрирования можно получить зависимости для определения времени наполнения рабочей камеры:

для режима докритического истечения

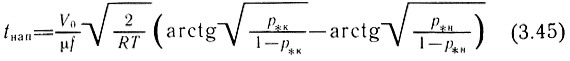
и для режима надкритического истечения

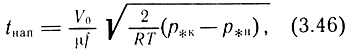
где V₀ - начальный объем подпоршневой полости; р_*н и р_*к - начальные и конечные значения относительного давления в камере; р_*н = р_н/р_вх; р_*к = рк/р_вх. Под конечным значением р_к понимается давление, при котором начинается движение поршня; р_н - начальное давление в рабочей полости (обычно р_н = р_ат).

Характер изменения давления в рабочей полости в период наполнения до начала движения определяется зависимостью (3.44), где расход G должен соответствовать режиму истечения.

При движении поршня во время рабочего цикла объем рабочей полости меняется от V_min до V_max при прямом ходе и от V_max до V_min при обратном ходе.

Рассмотрим уравнение состояния воздуха в рабочей полости при прямом ходе поршня. Масса воздуха в рабочей камере при движении поршня

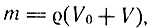
где V₀ - начальный объем рабочей полости; V - увеличение объема полости за счет движения поршня:

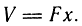
Как известно, ρ = p/(RT). Используя значение V и ρ, выражение для массы примет вид

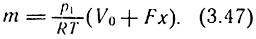
Рассмотрим изменение массы по времени:

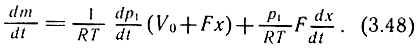
Однако изменение массы во времени представляет собой массовый расход, поэтому выражение (3.48) может быть представлено в виде

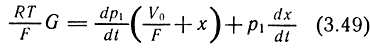
или

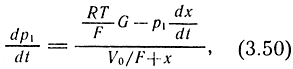
где G - расход воздуха в рабочую полость; определяется согласно режимам истечения по формулам (3.37) и (3.39); V₀/F - величина, постоянная для рассматриваемой конструкции привода.

Уравнение (3.50) определяет процесс изменения давления в рабочей полости при выполнении прямого хода поршня. Его решение возможно, если известны зависимости для переменной dx/dt.

Уравнение движения поршня с учетом действующих на него сил имеет вид

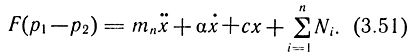
Здесь m_nх^⋅⋅ - сила преодоления инерционности массы подвижных частей привода (m_n); αх^⋅ - величина, учитывающая демпфирование, которое возникает при утечке воздуха между поршнем и стенками цилиндра; сх - величина, учитывающая сопротивление пружины; 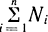- сумма сил, действующая на поршень (трение, постоянное внешнее усилие и др.).

В частности, для горизонтального расположения цилиндра привода величину 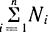можно представить как

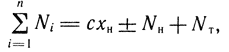
где сх_н - сила начального поджатия возвратной пружины; N_н - постоянная сила нагрузки на оси штока; N_т - сила трения.

В общем случае составляющие 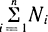определяются из условий эксплуатации привода.

Время перемещения поршня и давление в рабочей полости можно определить из совместного решения уравнений (3.50) и (3.51) и последующего интегрирования. Однако из-за сложности и нелинейности зависимости (3.50) на практике данная система уравнений решается численным интегрированием. Рассмотрим порядок выполнения его. На основе зависимостей (3.50) и (3.51) для малых промежутков времени и участков интегрирования исходную систему уравнений запишем в виде

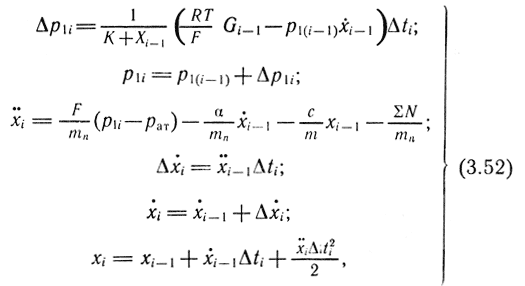
где k = V₀/F.

Величина р₂ в уравнении (3.51) принимает значение атмосферного давления р_ат, так как рассматривается прямой ход поршня, и правая полость в этом случае соединяется с атмосферой. Для одностороннего привода давление р₂ = Р_ат; Δt_i - шаг интегрирования, выбираемый из условий задачи, при этом с уменьшением Δt увеличивается точность интегрирования. Расход газа в рабочую полость определяется уравнениями (3.37) и (3,39) в соответствии с режимом истечения. Относительное давление р_* на каждом шаге интегрирования принимает различные значения, что необходимо учитывать при определении режима истечения. Индекс i указывает порядковый номер шага интегрирования.

Последовательность численного интегрирования:

1) начальные условия i = 0; х₀ = 0; р₁₀ = ΣN/F + P_ат; х^⋅₀ = 0; Δt_i = Δt₁.

Значение Δp₁ на первом участке Δp₁₁ определяется по первому уравнению системы (3.52);

2) по найденному значению Δp₁₁ находим p₁₁ (второе уравнение системы), которое определяет давление в рабочей камере через Δt₁, после подачи воздуха;

3) подставляя значение р₁₁ в третье уравнение, получим значение ускорения поршня х^⋅⋅₁₁ в конце первого временного шага;

4) последовательно решая четвертое - шестое уравнения, получим значения х₁₁ для положения поршня после истечения времени Δt₁.

Затем расчет повторяется для следующего шага времени Δt₂, Δt₃ и т. д. до тех пор, пока значение хода поршня не достигнет величины х = х_max, где x_max - максимальный ход поршня от упора до упора.

Максимальное время перекладки поршня из одного крайнего положения в другое при рабочем ходе определяется выражением

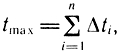
где n - число шагов интегрирования.

Как известно, составляющая(α/m)_nх^⋅_i-1 в третьем выражении системы (3.52) определяет демпфирование поршня при движении за счет утечек газа через уплотнения поршня. В приводах с хорошим качеством сборки и малым ресурсом наработки можно принять α = 0. Определение процессов обратного хода выполняется по зависимостям системы уравнений (3.52), при этом принимают начальные условия:

- объем рабочей камеры V_max = V₀ + х_maxF;

- давление в рабочей полости принимается равным давлению, которое устанавливается при достижении поршнем положения х = х_max.

Время опорожнения t_оп рабочей полости определяется при совместном решении уравнений (3.41), (3.42) и (3.44) в соответствии с режимом истечения:

- для надкритического режима истечения (р_ат/p₁ ≤ 0,5)

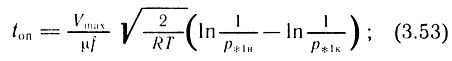
- для докритического режима истечения (р_ат/p₁ ≥ 0,5):

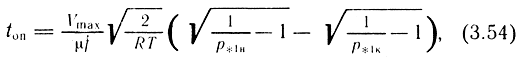
где р_*1н и р_*1к - относительные давления в рабочей полости соответственно в моменты открытия полости в атмосферу и начала движения поршня:

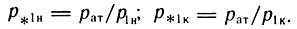
Уравнение (3.49) в случае обратного хода примет вид

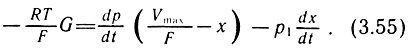
Знак минус в левой части равенства соответствует уменьшению массы газа в рабочей полости.

Поршневой пневмопривод двустороннего действия имеет тот же принцип действия и закономерности процессов, что привод одностороннего действия. Основное отличие - отсутствует возвратная пружина, а обратный ход обеспечивает сила давления сжатого воздуха во второй полости В цилиндра.

Левая и правая полости А и В (см. рис. 3.9) по функциональному назначению равнозначны и поочередно могут быть как рабочей, так и выхлопной. В каждой полости поочередно происходит процесс наполнения и опорожнения газа.

Динамика выходного звена привода описывается уравнением

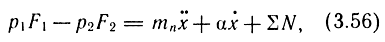
где р₁, F₁, p₂, F₂ - давление и рабочая площадь поршня соответственно в левой и правой полостях цилиндра.

Общие уравнения состояния привода будут иметь вид

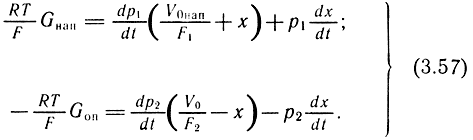
Совместное решение уравнений (3.56) и (3.57) позволяет оценить процесс изменения давления в каждой полости привода, определить время перемещения и координаты поршня в заданный момент времени. Порядок и методика решения этих уравнений аналогичны порядку и методике решения уравнений для одностороннего привода [см. (3.52)].