3.5. Пневматический следящий привод

Использование контурного управления для пневмопривода позволило бы решить многие проблемы и прежде всего позиционирования. Однако следящий пневмопривод не нашел широкого применения в практике промышленных роботов, что обусловлено рядом обстоятельств.

Конструкция следящего пневмопривода. Рассмотрим особенности конструкции и основные закономерности динамики следящего пневмопривода. Принципиальная схема такого привода представлена на рис. 3.10 а, б, где в качестве исполнительного двигателя используется цилиндр двустороннего действия с двусторонним штоком. Распределителем сжатого воздуха питания является струйный механизм, при отклонении которого вправо или влево пропорционально меняется расход воздуха в левую или правую полость цилиндра через сопла приемника. На оси струнника расположен якорь электромагнитного преобразователя (ЭМП) (на рисунке не указан). При равенстве токов управления i_у в обмотках управления наступает равновесие сил, действующих на якорь, при этом якорь и струйник находятся в среднем положении. При наличии разности токов управления равновесие сил нарушается, якорь и струйник поворачиваются на угол α, пропорциональный разности токов. Датчиком положения штока цилиндра является потенциометр обратной связи, где напряжение между средней точкой и одним из выводов питания определяет напряжение обратной связи u_о.с, пропорциональное положению штока. На рис. 3.10, б представлена структурная схема привода. Следящие пневмоприводы относятся к системам дроссельного управления, поскольку изменять расход на привод за счет изменения производительности компрессора неперспективно из-за высокой сжимаемости газа.

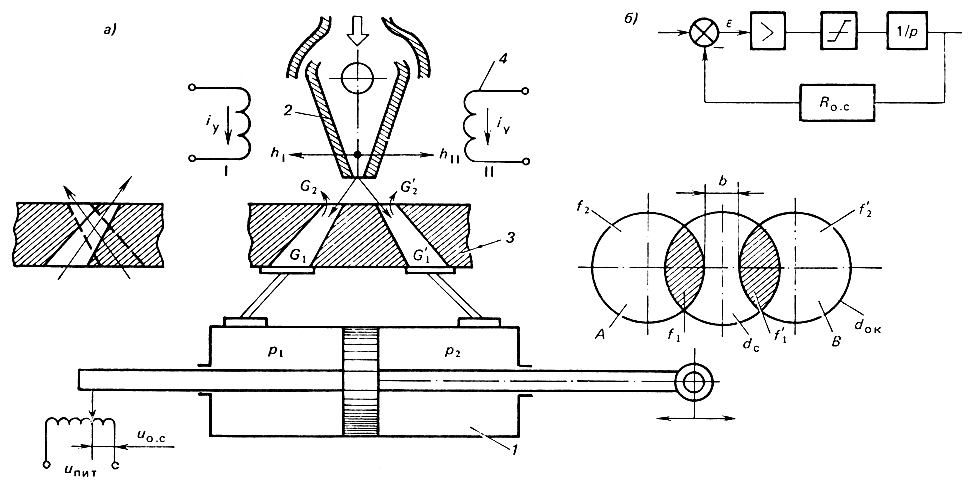
Рис. 3.10. Принципиальная схема следящего пневмопривода: 1 - цилиндр; 2 - струйный механизм; 3 - сопла приемника; 4 - обмотка управления

Принцип действия струйного пневмораспределителя основан на двойном преобразовании энергии:

- в струйной трубке потенциальная энергия сжатого газа преобразуется в кинетическую энергию потока струи газа;

- в приемных соплах приемника кинетическая энергия струи газа преобразуется в потенциальную энергию сжатого газа, поступающего в рабочие полости цилиндра.

Двойное преобразование энергии приводит к потерям давления до 10%. Конструктивно струйная трубка выполнена в виде конуса с углом у основания, равным 13°. Диаметр сопла на срезе трубки выбирают с учетом обеспечения необходимого расхода (обычно 0,5-2,5 мм). Ширина перемычки b влияет на чувствительность устройства и выполняется равной b = 0,14÷0,5 мм. Угол конусности составляет 10°. Для уменьшения реактивного действия вытекающей из окна струи воздуха приемные каналы располагают под углом в плоскости, перпендикулярной плоскости, проходящей через центры приемных окон (см. рис. 3.9, а). Минимальное расстояние между срезом струйной трубки и поверхностью приемника должно выбираться согласно зависимости 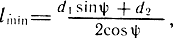где d₁ - диаметр торца струйной трубки; d₂ - диаметр приемного отверстия; ψ - угол наклона струи.

Диаметры приемных окон выбираются равными диаметру сопла трубки. Приращение диаметра окна по отношению к диаметру сопла допускается не более 0,1 мм, так как при этом увеличивается подсос воздуха из окружающей среды, уменьшаются скорость струи и давление в приемных окнах.

Эквивалентная схема проточных каналов и полостей привода представлена на рис. 3.11, а.

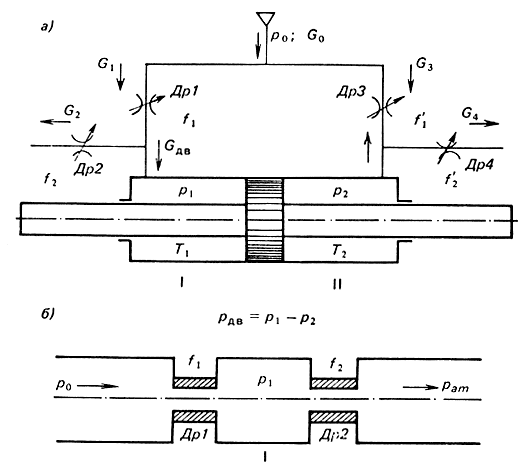
Рис. 3.11. Схема проточных каналов привода

Расход воздуха через струйную трубку зависит от режима истечения и определяется формулами:

- для докритического режима истечения (p_i/р₀ ≥ 0,5)

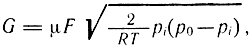
где p_i - давление в полости цилиндра;

- для надкритического истечения при р_i/р₀ ≤ 0,5

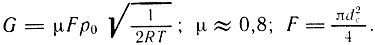
Эффективные площади наполнения и опорожнения приемных окон рассчитываются по формулам:

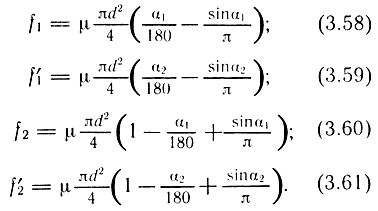
Здесь принято d = d₁ = d₂ = d_c;

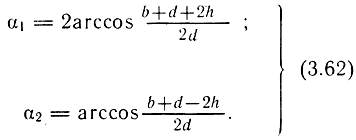
Характеристика привода. Статическая (нагрузочная) характеристика привода определяет зависимость давления в полостях рабочего цилиндра от входного управляющего сигнала. Так как отклонение струйной трубки h прямо пропорционально току управления, то обычно статическая характеристика определяется как функция

Данная характеристика определяется практически при заторможенном поршне.

Рассмотрим процесс наполнения и опорожнения левой полости цилиндра. Пусть струйная трубка занимает промежуточное положение, при котором f₁ - площадь наполнения, f₂ - площадь опорожнения приемного окна А. Эквивалентная схема левой полости дана на рис. 3.11, б.

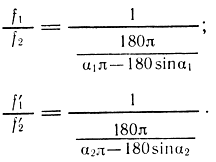
При установившемся режиме для докритического истечения расход сжатого воздуха через дроссель Др1 равен расходу опорожнения через дроссель Др2:

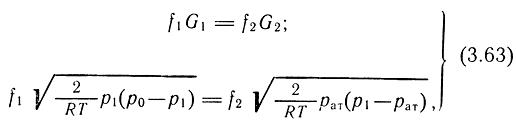
где f₁ и f₂ - эффективные площади турбулентных дросселей Др1, Др2; f₁ = μF₁; f₂ = μF₂; F₁ и F₂ - геометрические площади дросселей.

В общем случае в проточной камере происходит четыре, различных сочетания режимов истечения через дроссели Др1 и Др2:

1) докритическое истечение (ДИ) через дроссель Др1 и докритическое истечение через дроссель Др2 (ДИ1-ДИ2);

2) надкритическое истечение (НИ) через дроссель Др1 и докритическое истечение через дроссель Др2 (НИ1-ДИ2);

3) докритическое истечение через дроссель Др1 и надкритическое истечение через дроссель Др2 (ДИ1-НИ2);

4) надкритическое истечение через дроссель Др1 и надкритическое истечение через дроссель Др2 (НИ1-НИ2).

Найдем соотношения между площадями дросселей и давлениями в полостях цилиндра для каждого из четырех сочетаний режимов истечения.

1. Случай ДИ1-ДИ2 представим в относительных величинах [см.(3.63)]:

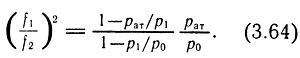
Введем обозначения: n = p_ат/p₀; n₁ = р_ат/р₁; n₂ = р₁/р₀, откуда n = n₁n₂ или n₁ = n/n₂, тогда выражение (3.64) при n₁ ≥ 0,5 и n₂ ≥ 0,5 будет иметь вид

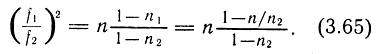
2. Случай НИ1-ДИ2. При n₁ ≥ 0,5 и n₂ ≤ 0,5

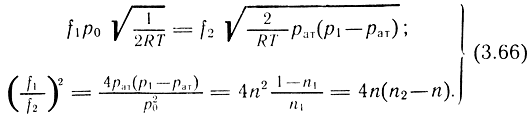
3. Случай ДИ1-НИ2. При n₁ ≤ 0,5 и n₂ ≥ 0,5

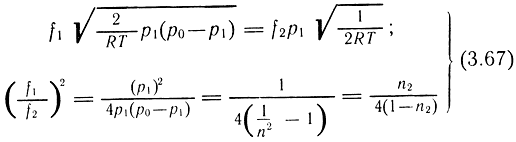
4. Случай НИ1-НИ2. При n₁ ≤ 0,5 и n₂ ≤ 0,5

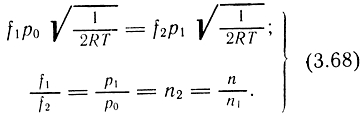
Задача расчета статической характеристики привода упростится, если с помощью соотношений (3.65)-(3.68) построить зависимость давления в полости цилиндра от площадей наполнения и опорожнения (рис. 3.12). На рисунке отмечены четыре зоны, соответствующие четырем рассмотренным случаям истечения.

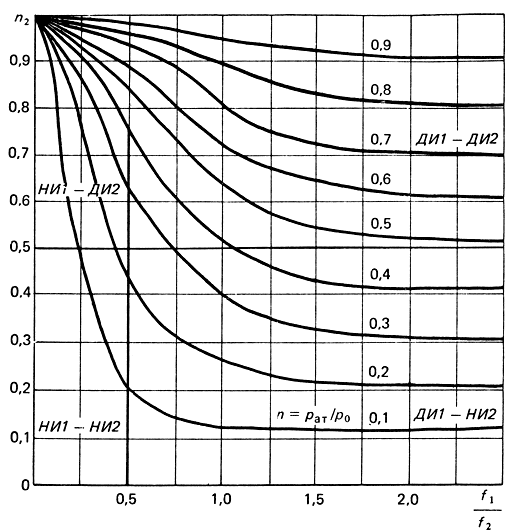
Рис. 3.12. График изменения давления в полостях рабочего цилиндра

Граница между зонами определяется подстановкой соответствующего значения n₁ и n₂ в уравнении (3.65)-(3.68). Статическая характеристика привода Δр = f(h) определяется совместным решением зависимостей (3.58)-(3.61) и (3.65)-(3.68), при этом, согласно (3.58)-3.61),

На рис. 3.13 приведена статическая характеристика привода, построенная в относительных величинах:

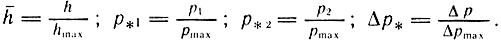
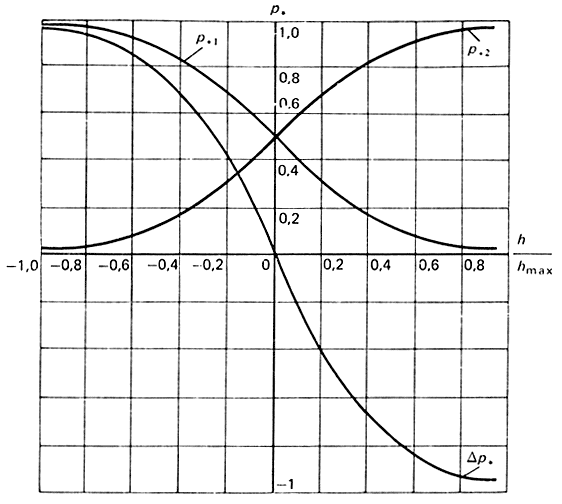
Рис. 3.13. Статическая характеристика Δр = f(h) привода

Дано: p₀ = 0,5 МПа; p_ат = 0,1 МПа; h_max = 1 мм; d = d₀ = d_A = d_B, b = 0,2 мм.

Анализ образцов ПР позволяет установить значения входного давления p₀ = 0,5÷0,6 МПа и давления выхлопа р_ат = 0,1 МПа. В соответствии с этим истечение из сопловой трубки будет надкритическим, так как p_ат/p₀ = 0,2 < 0,5.

В общем случае истечение в полость и из полости цилиндра будет изменяться от одного режима к другому, так как при этом могут быть различные начальные условия положения поршня и заполнения полостей. Как показали исследования, для следящего привода при нулевом управляющем сигнале h = 0 давление в полостях составляет величину p_1,2 ≈ 0,5p₀. При наличии управляющего сигнала h < h_max наполнение полости происходит при докритическом истечении p₁/p₀ ≥ 0,5, опорожнение второй полости происходит при надкритическом истечении р_ат/р₂ ≤ 0,5.

Расход сжатого воздуха при указанных условиях будет определяться по известным зависимостям для процессов наполнения и опорожнения соответственно:

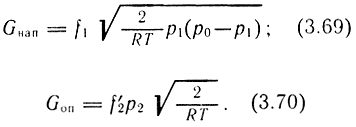
Динамика следящего пневмопривода. Для упрощения расчетов динамических характеристик привода с целью качественного анализа примем следующие допущения:

- давление на входе p₀ = const;

- расход через струйную трубку G_ст = const;

- коэффициент потерь μ = 1;

- приемник характеризуется линейной зависимостью изменения площади наполнения от смещения струйной трубки:

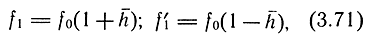
где 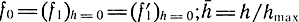- изменение давления в полостях цилиндра р₁ и р₂ при малых отклонениях струйной трубки прямо пропорционально изменению площади наполнения f₁:

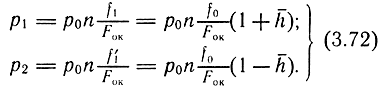
Здесь n - коэффициент потерь энергии, n = 0,9; F_ок - площадь приемных окон.

При h = 0, согласно зависимости (3.72), давление в полостях цилиндра

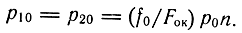
Если принять, что f_ок = 0,5F_ок, то p₁₀ = p₂₀ = 0,5p₀n. Перепад давления на поршне двигателя p_дв = p₁ - p₂ или с учетом зависимости (3.72)

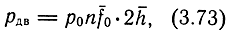
где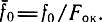

Приращение перепада давления на поршне

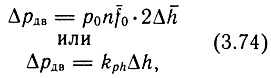
где

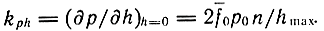
Рассмотрим зависимость расхода сжатого воздуха через двигатель в зависимости от сигнала управления и давления нагрузки.

Эквивалентная схема двигателя представляет собой соединение четырех переменных дросселей (см. рис. 3.11). Зависимости для расхода через каждый дроссель имеют вид:

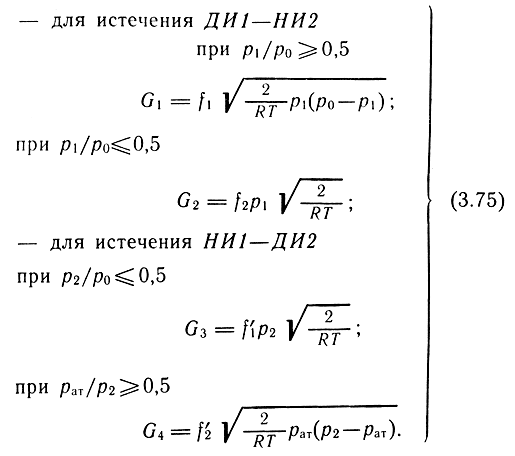
Данная система уравнений определена для сигнала h₁, т. е. струйник отклоняется влево.

Аналогично для сигнала h₁₁ расход определяется по следующим выражениям:

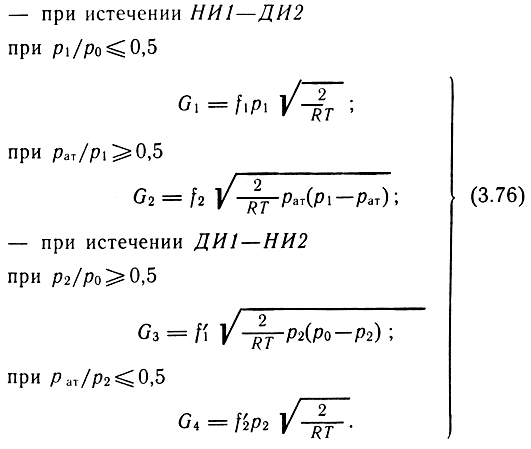
Полезный расход через двигатель в силу неразрывности потока определяется соотношениями

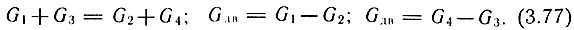
Давление питания можно определить из формулы (3.72) при f₀ = 0,5F_ок:

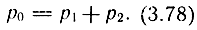
Учитывая, что р_дв = р₁ - р₂, из выражения (3.78) можно определить

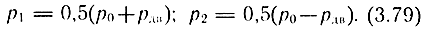
Решая совместно уравнения (3.71), (3.75), (3.77), (3.79) для h₁ и уравнения (3.71), (3.76), (3.77), (3.79) для h₁₁, получим выражение для расходной характеристики пневматического двигателя со струйным управлением:

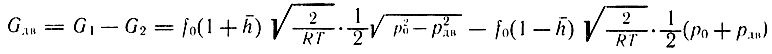
или

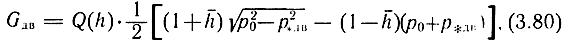
где 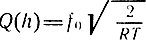- проводимость дросселя.

В относительных величинах выражение (3.80) имеет вид

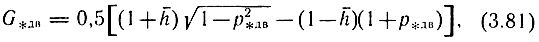
где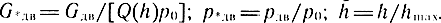

График расходной характеристики привода (3.81) представлен на рис. 3.14. Уравнение расходной характеристики пневматического двигателя позволяет установить, что с увеличением давления нагрузки расход через двигатель уменьшается при фиксированном сигнале управления h. Это явление, называемое дроссельным эффектом, снижает жесткость механической характеристики привода и вызывает скольжение поршня под действием внешней нагрузки. В частном случае, при р_*дв = 0, характеристика (3.81) преобразуется в характеристику регулирования расхода G_*дв = h¯ или

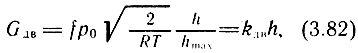
где

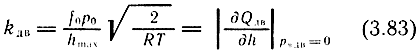
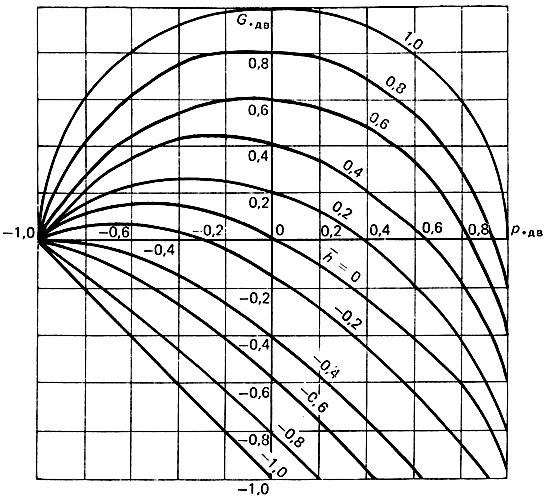
Рис. 3.14. Расходная характеристика привода

При заторможенном поршне (G_дв = 0) расходная характеристика преобразуется в нагрузочную характеристику:

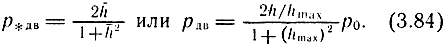
Графики зависимостей (3.82) и (3.84) представлены на рис. 3.15, а, б.

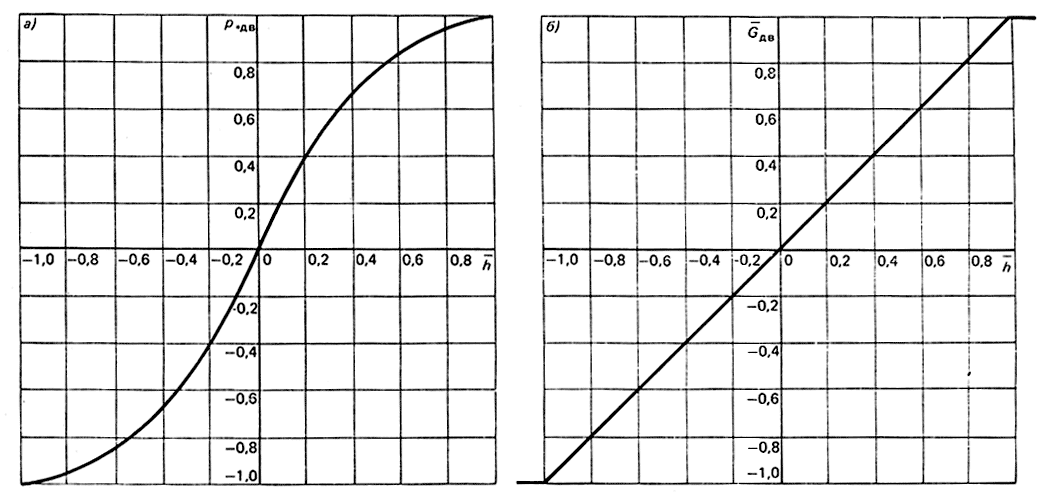
Рис. 3.15. Характеристики р_*дв = f(h¯), G¯_дв = f(h¯) привода

Угол наклона характеристики (коэффициент усиления по давлению) в начале координат имеет величину

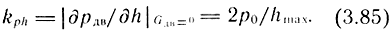
Расходная характеристика (3.81) представляет собой нелинейную функцию двух переменных 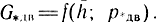Для упрощения анализа динамики привода выполним линеаризацию этой зависимости. С этой целью разложим функцию в ряд Тейлора в окрестности h¯ = 0; p_*дв = 0, так как функция является монотонной и непрерывной. Ограничимся членами разложения первого порядка малости. Линеаризованное уравнение расхода в приращениях будет иметь вид

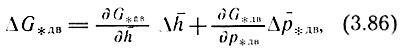
где ∂G_*дв/∂h¯ = k_дв - коэффициент усиления по расходу, увеличение данного коэффициента приводит к возрастанию коэффициента усиления системы управления, что сказывается на запасе устойчивости; ∂G_*дв/∂p_*дв = k_ск - коэффициент скольжения привода, определяет степень демпфирования колебаний привода; чем выше коэффициент, тем больше демпфирование.

Коэффициент усиления по расходу k_дв определяется зависимостью (3.84), коэффициент скольжения привода выражается частной производной выражения (3.81):

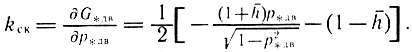
При р_*дв = 0, h¯ = 0 коэффициент скольжения определяется зависимостью

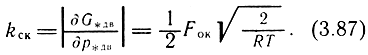
Рассмотрим вывод уравнения движения и передаточные функции пневмопривода со струйным управлением. За неизвестную переменную примем линейное перемещение выходного звена двигателя - штока y(t), входной сигнал - перемещение струйной трубки h(t); t - время. При выводе линеаризованного уравнения движения штока примем следующие допущения:

- динамический процесс рассматривается в окрестности установившегося движения относительно среднего положения поршня;

- сухое трение при движении поршня пренебрежимо мало.

Движение привода оценивается двумя уравнениями: динамики выходного звена и расхода сжатого воздуха через двигатель.

Уравнение динамики выходного звена

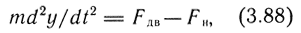
где m - масса движущихся частей (шток с поршнем + нагрузка); F_дв - движущее усилие, приложенное к штоку; F_н - сила сопротивления от нагрузки.

В этом случае

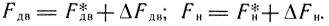
F^* - установившееся значение силы; ΔF - приращение силы; 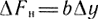- приращение сил вязкого трения (b - коэффициент вязкого трения).

В промышленных роботах основным видом нагрузки является инерционная нагрузка, т. е. имеет место в механизмах выдвижения, поворота.

Уравнение статики

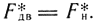
Уравнение динамики (3.88) в приращениях будет иметь вид

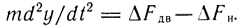
Для силового цилиндра

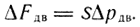
Здесь S - рабочая площадь поршня двигателя; Δp_дв - приращение перепада давления на поршень.

В соответствии с изложенными условиями

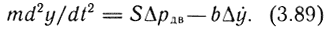
Данное уравнение составлено для одной степени свободы. Для робота с несколькими степенями свободы уравнение динамики описывается системой уравнений движения. Уравнение расхода сжатого воздуха учитывает равенство поступившего в двигатель расхода требуемому расходу по условию обеспечения заданного режима движения выходного звена

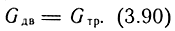
Здесь G_дв - расход через двигатель, определяемый зависимостью (3.81); G_тр - требуемый расход.

С учетом приращений зависимость (3.90) примет вид

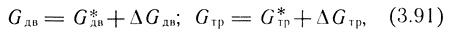
где G^* - установившееся значение расхода; ΔG - приращение расхода по условиям динамики привода.

Уравнение статики:

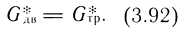
Из уравнений (3.90) и (3.91) получим

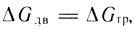
при этом ΔG_дв определяем из уравнения (3.87):

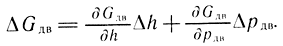
С учетом зависимостей (3.83) и (3.87):

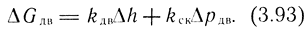
Уравнение расхода в полости наполнения

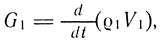
но 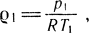откуда расход в полость наполнения будет определяться зависимостью

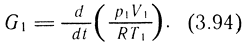
Уравнение (3.94) необходимо решать с уравнением энергии

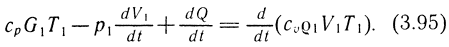
При этом принимается, что температура подводящего газа равна температуре газа в рабочей полости. Из совместного решения (3.94) и (3.95) следует, что

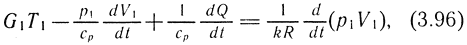
где 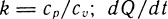- скорость теплопередачи от газа к стенкам цилиндра, на практике процесс в полости принимают адиабатным, т. е. теплообмен отсутствует. В этом случае процессы наполнения и опорожнения будут определяться следующими аналогичными зависимостями:

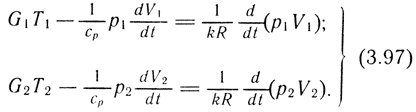
При малых отклонениях от установившегося режима

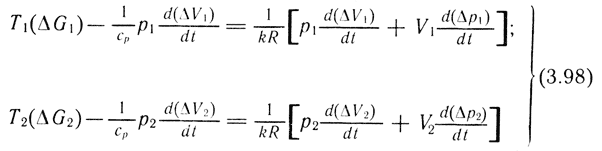
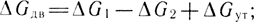
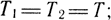
Принимая, что 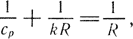можно определить

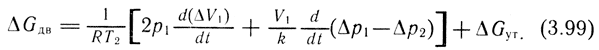
Изменение объема по времени d(ΔV)/dt проходит за счет движения поршня ΔV = SΔy, откуда выражение (3.99) будет иметь вид

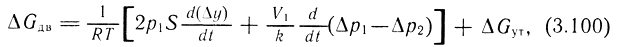
где 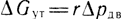- потери расхода на утечки через уплотнения поршня; r - коэффициент утечки;

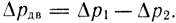
Система линеаризованных дифференциальных уравнений движения выходного звена двигателя на основании зависимостей (3.82), (3.93) и (3.100) может быть представлена следующим образом:

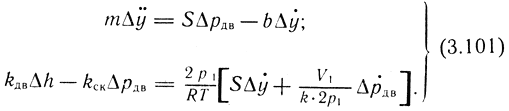
Для предварительного анализа динамики привода можно принять b = 0, т. е. вязкое трение пренебрежимо мало и утечки G_ут отсутствуют.

Решая совместно уравнения системы (3.101), можно получить

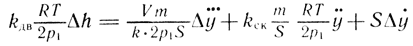
или в операторной форме

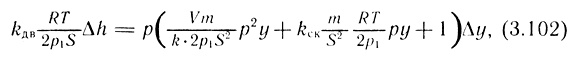
где p ≡ d/dt - оператор.

Введем условные обозначения:

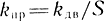
- коэффициент усиления привода по скорости при h = h^* и р_дв = 0;

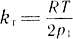
- коэффициент, характеризующий физические свойства рабочего тела;

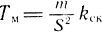
- механическая постоянная времени, учитывающая влияние нагрузки;

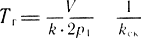
- газовая постоянная времени, учитывающая сжимаемость газа в рабочем объеме двигателя;

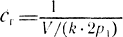
- коэффициент жесткости рабочего тела (газа) в полости двигателя, пропорционален давлению р в данном объеме, k = c_p/c_v, для воздуха k = 1,4;

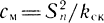
- коэффициент жесткости нагрузочной (механической) характеристики привода в окрестности установившегося значения h = h^*; р_дв = р^*_дв; Т_м = m/с_м; Т_г = с_м/с_г.

С учетом принятых обозначений

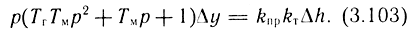
Приведем выражение (3.103) к стандартному виду колебательного звена:

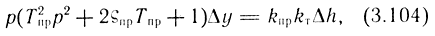
где 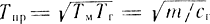- постоянная времени привода;

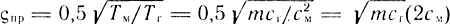
- коэффициент демпфирования.

Выполнив преобразование по Лапласу зависимости (3.104) при нулевых начальных условиях, можно получить передаточную функцию системы от перемещения струйной трубки h к перемещению выходного звена двигателя y:

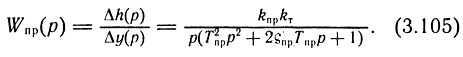
Анализ выражения (3.105) для передаточной функции пневмопривода со струйным устройством управления позволяет установить, что динамические свойства привода оцениваются:

- коэффициентом усиления привода по скорости k_пр;

- коэффициентом физического состояния рабочего тела k_т;

- постоянной времени привода Т_пр;

- коэффициентом демпфирования ς_пр.

Коэффициент усиления привода по скорости 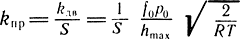характеризует крутизну нарастания расхода при перемещении струйной струбки. Коэффициент увеличивается с возрастанием давления питания р₀ и площади наполнения и опорожнения.

Увеличение коэффициента физического состояния тела k_т приводит к повышению общего коэффициента усиления привода k_c = k_прk_т, что достигается за счет роста температуры рабочего тела.

Постоянная времени привода Т_пр определяет сопрягаемую частоту ω_пр = 1/Т_пр (как системы регулирования), частоту собственных колебаний 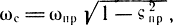а следовательно, и быстродействие привода.

При уменьшении постоянной времени привода Т_пр улучшаются динамические характеристики. Уменьшение Т_пр достигается, главным образом, за счет увеличения жесткости рабочего тела, что осуществляется повышением давления в полости.

Коэффициент демпфирования привода 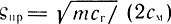увеличивается при уменьшении жесткости нагрузочной характеристики, т. е. с увеличением скольжения поршня под действием нагрузки. В дроссельном пневмоприводе коэффициент с_м достаточно велик вследствие малости k_ск, а коэффициент с_г достаточно мал вследствие большой сжимаемости рабочего тела. Следовательно, коэффициент демпфирования ς_пр << 1, что свидетельствует о слабом демпфировании и большой колебательности.

На основе системы уравнений (3.101) может быть составлена структурная схема привода (рис. 3.16).

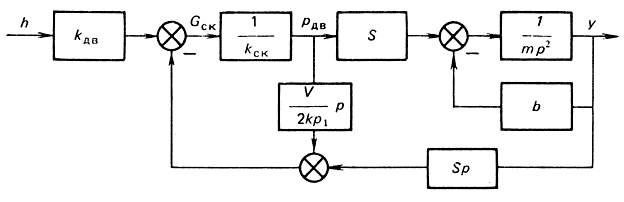
Рис. 3.16. Структурная схема привода

Исследование устойчивости привода как системы управления выполняется методами и средствами теории автоматического управления.

В пневмоприводах ПР в качестве рабочего тела используется сжатый воздух с температурой окружающей среды t ≈ 20°С и давлением питания p_o = 0,4÷0,6 МПа. Указанные параметры воздуха настолько ухудшают динамические характеристики следящего пневмопривода, что использование его в ПР является до настоящего времени технической проблемой. Однако это утверждение не настолько категорично, чтобы не искать методов улучшения характеристик привода. Так, имеются разработки по увеличению коэффициента демпфирования путем введения гибкой обратной связи по нагрузке.

В целом решение использования следящего пневмопривода заключается в разработке методики и создании конструкции.