
4.3. Исследование динамики системы управления электропривода
В общем случае система управления электропривода ПР состоит из трех контуров регулирования (см. рис. 4.3): тока, скорости и положения (угла поворота θ). Каждый из контуров представляет собой систему автоматического управления. Существуют различные варианты построения этих систем, т. е. различные контуры могут быть как аналоговыми, так и цифровыми. В рассмотренном на рис. 4.3 варианте функциональной схемы привода системы регулирования тока и скорости - аналоговые, а система регулирования угла - цифровая.
Система регулирования тока и скорости сервопривода. Различные методики расчета сервоприводов подробно описаны в работе [9]. Рассмотрим общие вопросы исследования динамики сервопривода на примере двухконтурной системы подчиненного регулирования скорости двигателя постоянного тока с вентильным преобразователем. Структурная схема такой системы приведена на рис. 4.21. Она соответствует линеаризованной модели системы, в которой нелинейности типа "зона нечувствительности" двигателя, "насыщение" преобразователя и усилителей и "люфт" механических передач не учитываются. Передаточные функции основных элементов схемы были определены в предыдущем параграфе, а характеристики регуляторов скорости и тока будут выбраны исходя из требований: 1) точности в установившемся режиме, 2) качества переходного процесса.
Структурная схема двигателя постоянного тока (рис. 4.21) по существу соответствует передаточной функции второго порядка, приведенной в § 4.2. Однако здесь для удобства расчетов она представлена в виде двух блоков, описывающих электрические (с постоянной времени Тэ) и электромеханические (с постоянной времени Tм) свойства двигателя и блока обратной связи с коэффициентом усиления k2, который учитывает влияние изменения момента нагрузки на валу двигателя на изменение тока якоря. Постоянная времени Тм учитывает также инерционные свойства объекта (манипулятора). Через Iст на рис. 4.21 обозначен ток, обусловленный статической нагрузкой.
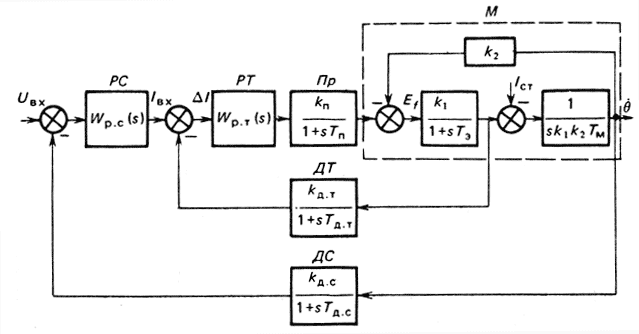
Рис. 4.21. Структурная схема двухконтурной системы регулирования (сервопривода)
Точность в установившемся режиме. Точность определяется методом коэффициентов ошибок [11]. Согласно данному методу, ошибка ε(t) в установившемся режиме εуст в системе, представленной на рис. 4.22, определяется выражением
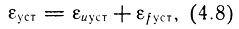
где установившаяся ошибка от сигнала уставки u(t) определяется соотношением
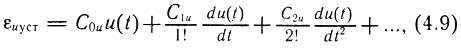
а установившаяся ошибка от возмущения f(t) определяется соотношением
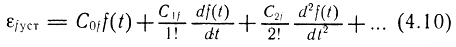
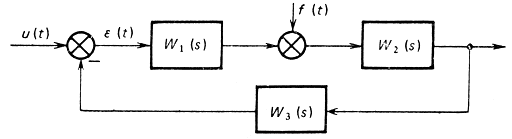
Рис. 4.22. Структурная схема системы, состоящей из регулятора, объекта, датчика: u(t) - сигнал управления; f(t) - возмущение
Коэффициенты Ciu и Сif (i = 0, 1, 2, ...) называются коэффициентами ошибок и определяются следующим образом:
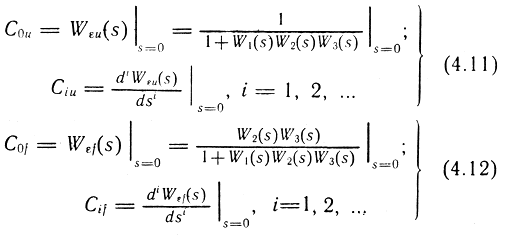
Как видно из рис. 4.21, контур регулирования тока содержит три апериодических звена с постоянными времени Tп, Tэ, Гд. т. Поэтому если в качестве регулятора тока использовать П-регулятор (§ 4.2), то получим статическую систему с установившейся ошибкой ΔIIвх по управлению от постоянного входного воздействия Iвх. Ошибка, согласно (4.9) и (4.11), определяется соотношением
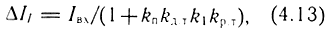
где Kр.т - коэффициент, усиления регулятора тока.
В случае ПИ-регулятора тока ошибка
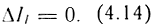
Ошибки ΔIf от действия возмущения Ef (см. рис. 4.21), согласно (4.10), (4.12), для П- и ПИ-регулятора определяются соотношениями
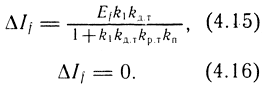
Аналогично могут быть рассчитаны установившиеся значения ошибки в контуре регулирования скорости. Для этого преобразуем схему (см. рис. 4.21) к более простому виду (рис. 4.23). На рисунке Wдв(s) - передаточная функция двигателя, полученная на основе структурного преобразования схемы:
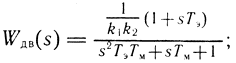
Wкт(s) - передаточная функция замкнутого контура регулирования тока:
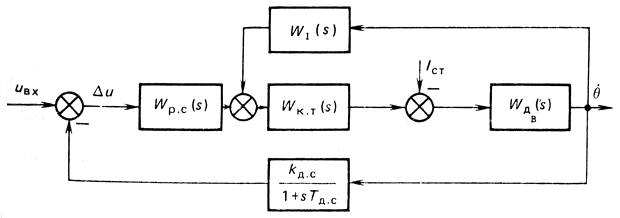
Рис. 4.23. Структурная схема контура регулирования скорости
- для П-регулятора тока
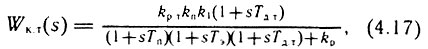
где kp = kp.тkпk1kд.т - коэффициент усиления разомкнутой системы регулирования тока;
- для ПИ-регулятора тока, когда Wп7т(s) = (1 + sTр.т/sTр.т,
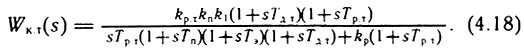
Передаточная функция
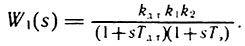
Согласно рис. 4.23 и соотношениям (4.9), (4.11), (4.17), (4.18), выражение для определения ошибки по управлению от uвх в контуре регулирования скорости запишется в виде:
- для П-регулятора скорости и П-регулятора тока
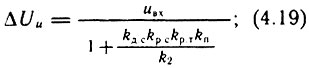
- для П-регулятора скорости и ПИ-регулятора тока
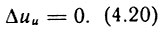
Для ПИ-регулятора скорости, когда 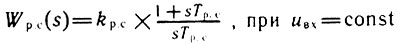
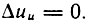
Ошибка Δu1 от возмущения Iс.т определяется исходя из рис. 4.23 и соотношений (4.10), (4.12), (4.17), (4.18):
- для П-регулятора скорости и П-регулятора тока
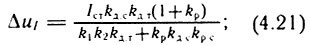
- для П-регулятора скорости и ПИ-регулятора тока
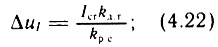
- для ПИ-регулятора скорости при Iст = const
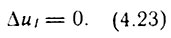
Полученные соотношения позволяют оценить точность сервопривода (суммарную установившуюся ошибку от действия сигнала управления и сигнала возмущения) и таким образом выбрать тип регуляторов.
Устойчивость и косвенная оценка качества регулирования. После того как выбран тип регуляторов тока и скорости, исходя из точностных характеристик, следует рассчитать их параметры (коэффициенты усиления и постоянные времени) из условия устойчивости и требований к качеству переходного процесса. Для этого удобно пользоваться логарифмическими амплитудно- и фазочастотными характеристиками (ЛАЧХ, ЛФЧХ) [7, 11]. Пользуясь ЛАЧХ, ЛФЧХ разомкнутой системы, можно исследовать области устойчивости замкнутой системы, оценить быстродействие, перерегулирование, а также рассчитать корректирующие звенья. Методика исследования на основе ЛАЧХ и ЛФЧХ детально разработана и подробно описана в учебных пособиях по теории автоматического управления. Здесь ограничимся приведением лишь кратких и наиболее полезных для практических расчетов сервоприводов сведений.
Исследуемая система регулирования (например, система регулирования тока или скорости) устойчива, если ЛАЧХ разомкнутой системы пересекает ось частот раньше, чем ЛФЧХ пересекает уровень - π.
Для оценки показателей качества переходного процесса рассмотрим некоторые простые правила, определяющие связь между ЛЧХ и данными показателями:
1) динамические свойства системы определяются в основном участками ЛАЧХ, близкими к частоте среза ωс. Эта частота соответствует пересечению ЛАЧХ с осью частот;
2) с ростом частоты среза увеличивается быстродействие системы (уменьшается время регулирования tp).
Приближенно связь ωс и tp может быть определена соотношением [11]
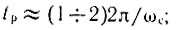
3) в правильно спроектированной системе наклон ЛАЧХ должен составить - 20 дБ/дек. Длина участка с наклоном - 20 дБ/дек должна быть не менее 1 дек;
4) для обеспечения перерегулирования 10-30% необходимо обеспечить запас по фазе γс = 30÷50° на частоте среза ωс и запас по амплитуде около 20 дБ. На рис. 4.24 приведены примеры ЛАЧХ и ЛФЧХ разомкнутой системы при различных коэффициентах передачи и соответствующие им переходные функции замкнутой системы hc(t);
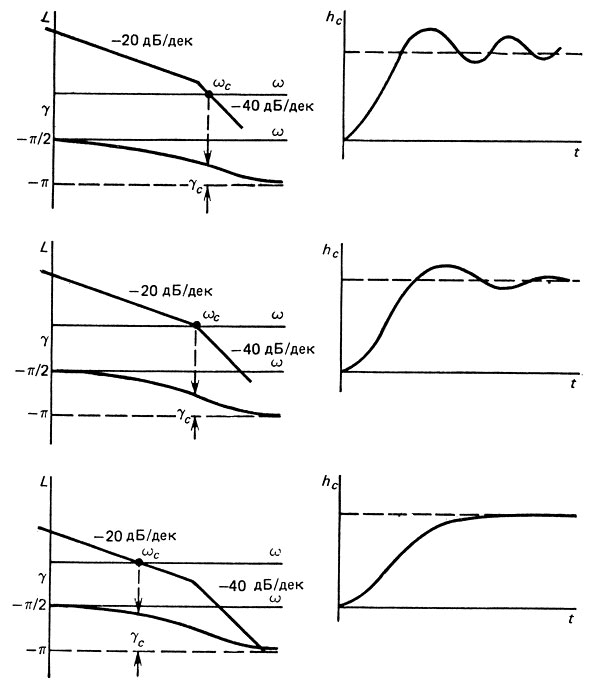
Рис. 4.24. Примеры ЛАЧХ и ЛФЧХ разомкнутой системы и соответствующие им переходные функции hc(t) замкнутой системы
5) если показатель колебательности В системы (т. е. относительное значение максимума амплитудно-частотной характеристики) больше единицы, то частотную характеристику исследуемой системы можно аппроксимировать колебательным звеном второго порядка [11]. Для этого случая зависимость перерегулирования σ, %, от показателя колебательности В приведена на рис. 4.25. А на рис. 4.26 приведены кривые, устанавливающие связь σ, %, В и запаса по фазе γc от коэффициента демпфирования колебательного звена.
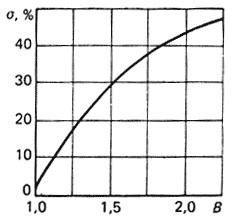
Рис. 4.25. Зависимость перерегулирования σ от показателя колебательности В
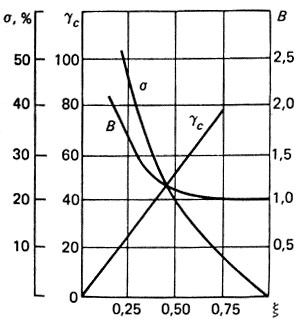
Рис. 4.26. Зависимость перерегулирования σ, показателя колебательности В и запаса по фазе γс от коэффициента демпфирования
Для полного анализа динамических характеристик сервопривода необходимо оценить влияние нелинейностей контуров регулирования тока и скорости. Для этого удобно пользоваться методом гармонического баланса [11], с помощью которого можно определить области существования и параметры периодических колебаний за счет влияния нелинейностей.
Условие гармонического баланса имеет вид
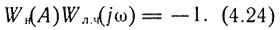
Здесь Wн(A) - эквивалентный комплексный коэффициент усиления нелинейного элемента; А, ω - амплитуда и частота гармонического сигнала на входе нелинейного элемента; Wл.ч(j, ω) - частотная характеристика линейной части системы.
Уравнение (4.24) удобно решать графически, находя решение как точку пересечения кривых Wл.ч(jω) и - Wн-1(А) (рис. 4.27). Для этого в табл. 4.9 приведены нормированные характеристики для нелинейностей типа "зона нечувствительности", "насыщение", "люфт".
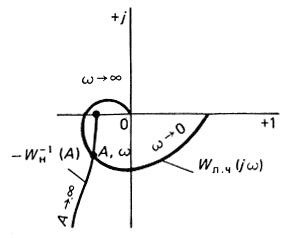
Рис. 4.27. Графическое решение уравнения гармонического баланса
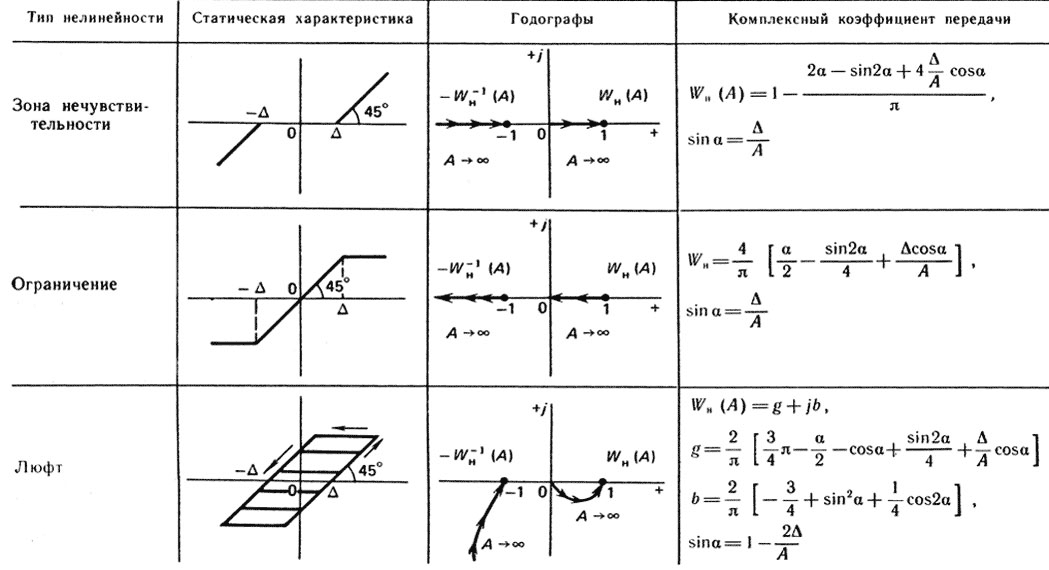
Таблица 4.9
Таким образом, пользуясь изложенной методикой, можно провести достаточно полное исследование динамики сервопривода:
1) определить точность и соответственно выбрать тип регулятора (П- или ПИ-регулятор); 2) определить параметры настройки регуляторов тока и скорости (или при необходимости параметры дополнительных корректирующих звеньев) исходя из условий устойчивости, отсутствия периодических колебаний и требований к качеству переходного процесса.
Цифровая система регулирования положения (угла). Будем считать, что параметры регулятора скорости и тока выбраны и, следовательно, известна передаточная функция двухконтурной системы регулирования скорости Wд.с(s). Рассмотрим структурную схему третьего контура (см. рис. 4.3), т. е. цифровой системы регулирования угла. Для преобразования непрерывного сигнала в дискретный в цифровой системе осуществляется квантование сигнала по уровню и времени. Поэтому на структурной схеме (рис. 4.28) это преобразование представлено последовательным соединением нелинейного элемента квантования по уровню (НЭ) и импульсного элемента (ИЭ) с тактом работы Т. Статическая характеристика НЭ показана на рис. 4.29. Цифровой сигнал ошибки Δθ'* равный разности цифровых значений заданного θз* и контролируемого θ* углов, поступает на преобразователь код - аналог, представляющий собой фильтр, называемый фиксатором нулевого порядка и имеющий передаточную функцию
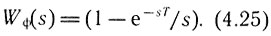
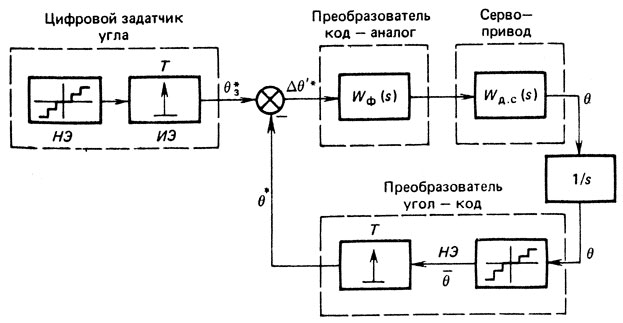
Рис. 4.28. Структурная схема цифрового привода
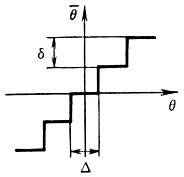
Рис. 4.29. Статическая характеристика нелинейного элемента квантования по уровню
Как видно из рис. 4.28, цифровая система является нелинейной импульсной системой, исследование которой в общем случае представляет значительные сложности. Существенное упрощение можно получить, если пренебречь квантованием по уровню что справедливо, когда в системе используются многоразрядные цифровые датчики, В этом случае цифровая система представляет собой линейную импульсную систему (рис. 4.30), методы исследования которой детально разработаны в. теории автоматического управления [7, 11].

Рис. 4.30. Эквивалентная структурная схема цифрового привода без учета квантования по уровню
Во многих случаях схема, приведенная на рис. 4.30, может быть упрощена. Действительно, если такт работы импульсного элемента Т существенно меньше постоянных времени сервопривода (см. рис. 4.28), то линейная импульсная система может рассматриваться как непрерывная, у которой передаточная функция в разомкнутом состоянии определяется соотношением
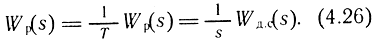
Если оказывается, что квантованием по уровню пренебречь нельзя, то цифровую систему следует анализировать с позиций теории нелинейных систем. Для этого случая условие абсолютной устойчивости цифровой системы формируется следующим образом: цифровая система устойчива, если при устойчивой приведенной непрерывной части с передаточной функцией 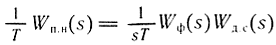 через точку - Δ/2δ; j0 можно провести прямую так, чтобы годограф модифицированной частотной характеристики Wп.н(jω) лежал справа от нее. Здесь
через точку - Δ/2δ; j0 можно провести прямую так, чтобы годограф модифицированной частотной характеристики Wп.н(jω) лежал справа от нее. Здесь
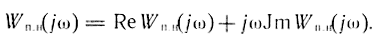
Для общего случая, когда приходится учитывать квантование по времени и уровню, критерий абсолютной устойчивости можно сформулировать по аналогии с [11] следующим образом: положение равновесия цифровой системы устойчиво, если устойчива приведенная непрерывная часть, а годограф частотной характеристики импульсной системы Wп.н*(jω), ω = ωT располагается справа от вертикальной прямой, проходящей через точку - Δ/2δ; j0.
Преобразуем структурную схему (см. рис. 4.28) к схеме, показанной на рис. 4.31, включив в нее дополнительно регулятор положения с передаточной функцией Wр.п(s) и отразив внешним воздействием F, приведенным ко входу сервопривода, влияние нагрузки на валу двигателя, kд.у - статический коэффициент передачи датчика угла.
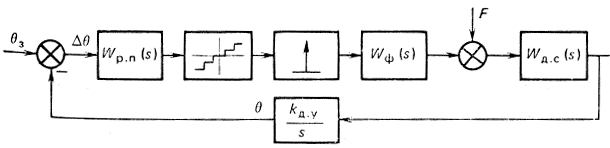
Рис. 4.31. Структурная схема электропривода с цифровым регулятором положения
Проведем предварительный анализ по линеаризованной модели системы. Так как система является астатической, то, согласно (4.11), ошибка от управляющего воздействия (θз = const) равна нулю. Однако наличие возмущения F, меняющегося в приводах ПР в широком диапазоне, может вызвать значительную ошибку ΔθF, устранение которой возможно двумя способами:
1) введением цепи компенсации возмущения, т. е. созданием комбинированной системы регулирования по отклонению и возмущению;
2) введением ПИ-регулятора положения.
При первом способе, который является достаточно простым и эффективным, не обеспечивается полной компенсации ошибки. Техническая реализация цепи компенсации при этом возможна даже на этапе создания сервопривода.
При втором способе ошибки ΔθF теоретически становится равной нулю, а система становится астатической второго порядка.
Анализ системы, использующей цифровой ПИ-регулятор, возможен по линеаризованной модели, в которой нелинейный элемент квантования по уровню заменяется линейным.
Известно, что замкнутая линейная система, содержащая в контуре два аналоговых интегратора, может быть устойчивой за счет введения корректирующих элементов. Если в такой системе кроме двух аналоговых интеграторов существует нелинейный элемент квантования с разрывной характеристикой, то это может привести к возникновению периодических колебаний. Это можно показать, решая уравнение (4.24) для схемы, приведенной на рис. 4.31, или объяснить, анализируя физические процессы в системе. Действительно, если даже предположить, что система находится в положении равновесия, то любое сколь угодно малое возмущение или дрейф нуля аналоговых интеграторов выведет систему из этого положения; при срабатывании нелинейного элемента квантования система вновь возвратится в исходное положение, при котором она представляет собой разомкнутую систему с двумя интеграторами, и далее процессы повторятся.
Использование цифровых интеграторов позволяет, во-первых, по существу исключить влияние нелинейного элемента квантования (т. е. заменить его линейным) и, во-вторых, исключить дрейф нуля интеграторов. С помощью цифровых интеграторов легко реализуются различные дискретные регуляторы и корректирующие элементы, построение которых рассматривается в следующем параграфе.
Учитывая сложность передаточной функции линейной части системы (рис. 4.31), необходимо тщательно проанализировать и влияние нелинейностей, показанных в табл. 4.9, на динамику системы. Это важно и с точки зрения точности в установившемся режиме. Даже в астатической системе возможна ошибка, определяемая нелинейностями типа "зона нечувствительности" или "квантование по уровню". Эта ошибка составляет ±Δ/2, где Δ - порог квантования (см. рис. 4.29) или зона нечувствительности (см. табл. 4.9).
|
ПОИСК:
|
© ROBOTICSLIB.RU, 2001-2019
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://roboticslib.ru/ 'Робототехника'