4.4. Дискретные регуляторы и корректирующие устройства

В предыдущем параграфе была показана целесообразность применения цифровых регуляторов положения, имеющих интегральную составляющую закона управления. Указывалось также, что в ряде случаев коррекция привода по скорости может быть реализована путем дифференцирования сигнала с датчика положения. Следовательно, цифровой регулятор может представлять собой ПИД-регулятор, закон управления которого реализуется алгоритмически ЦВМ.

ЦВМ преобразует входную последовательность чисел x[nТ] в выходную u[nТ] в соответствии с программой вычислений, представляющей собой алгоритм или закон управления.

В общем виде широкий класс линейных законов управления может быть описан разностным уравнением вида

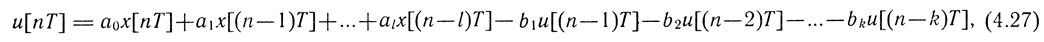
где Т - период дискретности (шаг выдачи данных ЦВМ); l - число запоминаемых значений величин, поступающих на ЦВМ; k - число запоминаемых значений выходного сигнала ЦВМ.

Уравнение (4.27) можно записать в сокращенной форме:

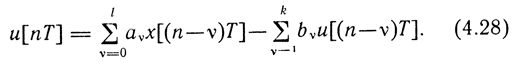
С помощью z-преобразования [11] от выражения (4.28) можно перейти к дискретной передаточной функции регулятора и корректирующего устройства:

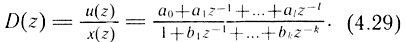
Для построения цифрового ПИД-регулятора необходимо реализовать на ЦВМ интегрирующее, пропорциональное безынерционное и дифференцирующее звенья. В табл. 4.10 приведены непрерывные и дискретные передаточные функции и соответствующие им разностные уравнения и переходные характеристики этих звеньев. Так, интегрирующее звено реализуется путем записи в ячейку R числа, равного сумме содержимого этой ячейки и входного числа из ячейки X:

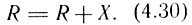
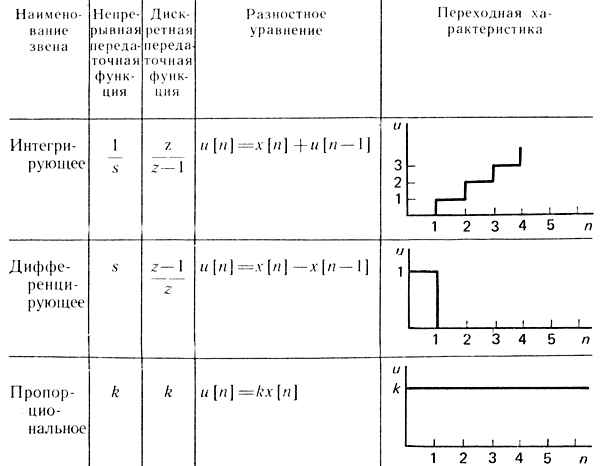
Таблица 4.10

Дифференцирующее звено реализуется следующим образом. В ячейку Х1 заносится значение X на предыдущем шаге, в ячейку R1 заносится разность содержимого X и X1:

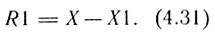
Пропорциональное звено реализуется путем умножения содержимого X на постоянный коэффициент К:

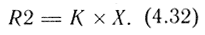
ПИД-закон регулирования реализуется путем суммирования содержимых ячеек R, R1, R2, умноженных на соответствующие коэффициенты:

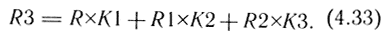
Таким образом, для построения на ЦВМ произвольного корректирующего звена, реализующего требуемый закон управления, следует: 1) определить дискретную передаточную функцию вида (4.29) по непрерывной передаточной функции звена;

2) записать разностное уравнение вида (4.27), определив в (4.29) коэффициенты а₀, ..., а_l и b₁, ..., b_k;

3) составить программу вычислений на ЦВМ в соответствии с разностным уравнением.

В табл. 4.11 приведены непрерывные и дискретные передаточные функции, разностные уравнения и переходные характеристики некоторых типовых корректирующих звеньев.

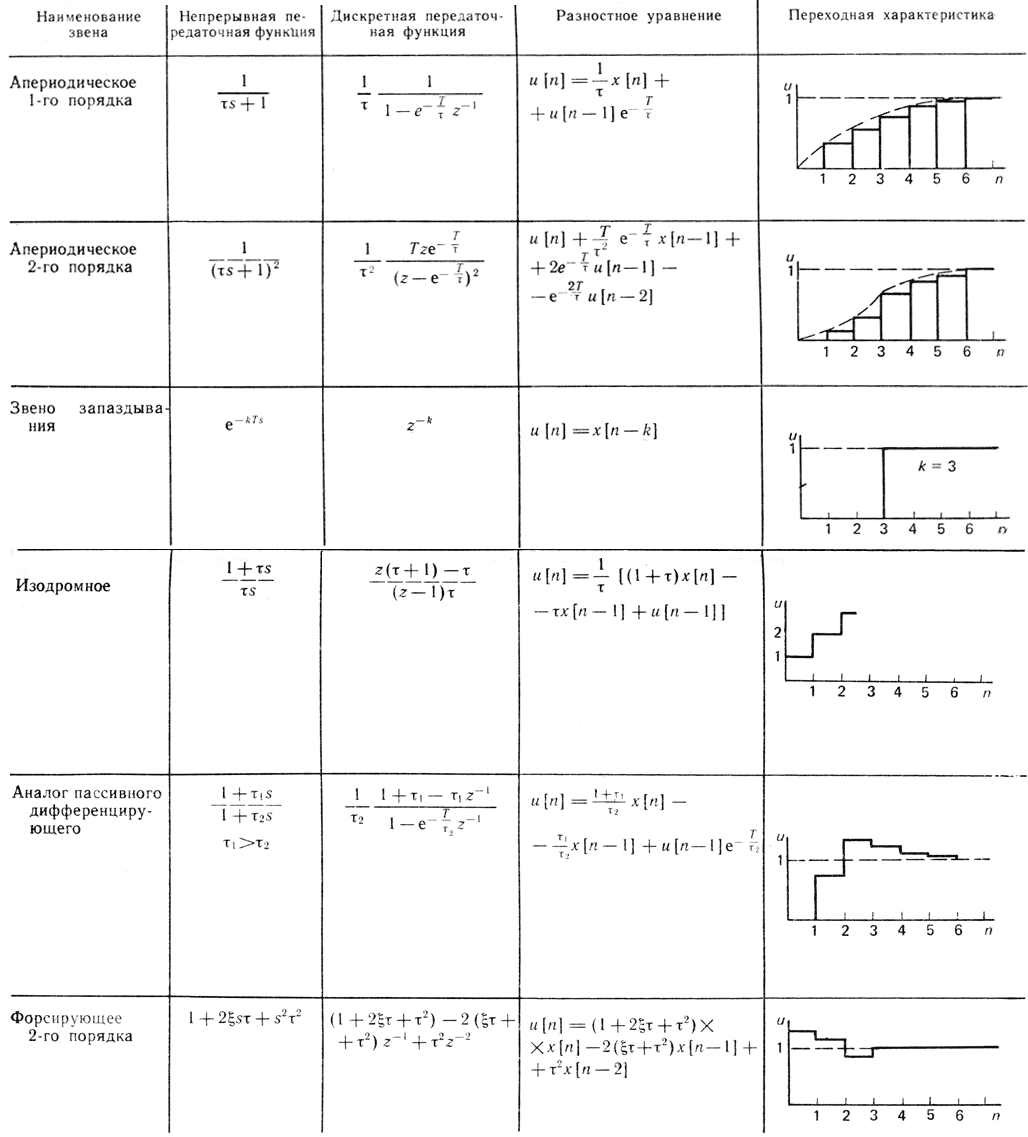
Таблица 4.11

Дискретные корректирующие устройства рассчитываются так же, как и корректирующие устройства непрерывного действия. Например, передаточная функция последовательного дискретного корректирующего устройства определяется соотношением

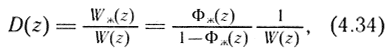
где W_ж(z) и W(z) - дискретные передаточные функции желаемой и нескорректированной разомкнутых систем; Φ_ж(z) - передаточная функция желаемой замкнутой системы.

Для выполнения условия физической реализуемости дискретного корректирующего звена необходимо учитывать следующие ограничения:

1) дискретная передаточная функция желаемой замкнутой системы Φ_ж(z) должна содержать в качестве нулей все те нули передаточной функции W(z), модули которых равны или больше единицы;

2) функция 1-Φ_ж(z) должна содержать в качестве нулей все те полюсы передаточной функции W(z), модули которых равны или больше единицы.

Невыполнение этих условий приводит к нарушению грубости системы и ее неустойчивости, так как при этом получаются неустойчивые линейные программы ЦВМ [см. (4.27)], соответствующие передаточной функции (4.34). Кроме того, получающаяся дробно-рациональная функция D(z) не должна иметь степень числителя выше степени знаменателя, так как это приводит к необходимости располагать в данный момент времени будущим значением входного сигнала, что, естественно, не может быть реализовано.